Giải Bài Tập SGK Toán Lớp 8 Bài 7: Hình Bình Hành

Giải Toán 8 bài 7 Hình bình hànhGiải bài tập SGK Toán lớp 8 bài 7Bài trướcTải vềBài sauNâng cấp gói Pro để trải nghiệm website VnDoc.com KHÔNG quảng cáo, và tải file cực nhanh không chờ đợi. Mua ngay Từ 79.000đ Tìm hiểu thêm

Giải bài tập Toán 8 bài 7 Hình bình hành

• Câu hỏi 1 trang 90 SGK Toán 8 tập 1
• Câu hỏi 2 trang 90 SGK Toán 8 tập 1
• Câu hỏi 3 trang 92 SGK Toán 8 tập 1
• Bài 43 trang 92 SGK Toán 8 Tập 1
• Bài 44 trang 92 SGK Toán 8 Tập 1
• Bài 45 trang 92 SGK Toán 8 Tập 1
• Bài 46 trang 92 SGK Toán 8 Tập 1
• Bài 47 trang 93 SGK Toán 8 Tập 1
• Bài 48 trang 93 SGK Toán 8 Tập 1
• Bài 49 trang 93 SGK Toán 8 Tập 1

Giải Toán 8 bài 7 Hình bình hành được VnDoc chia sẻ dưới đây bao gồm các bài giải tương ứng với từng bài học trong SGK Toán 8 tập 1, giúp cho các bạn học sinh ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải Toán 8. Mời các bạn tham khảo.

Câu hỏi 1 trang 90 SGK Toán 8 tập 1

Các cạnh đối của tứ giác ABCD trên hình 66 có gì đặc biệt?

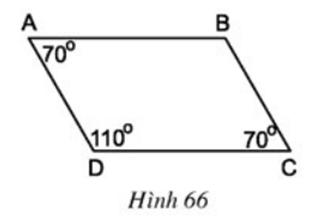
Lời giải

Các cạnh đối của tứ giác ABCD bằng nhau và song song với nhau

(Nhận xét trang 70: Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau)

Câu hỏi 2 trang 90 SGK Toán 8 tập 1

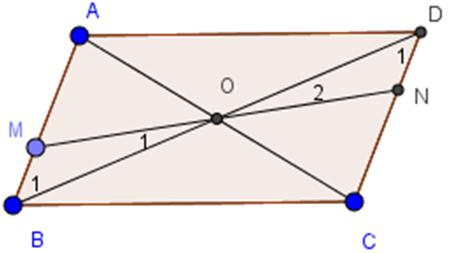
Cho hình bình hành ABCD (h.67). Hãy thử phát hiện tính chất về cạnh, về góc, về đường chéo của hình bình hành đó.

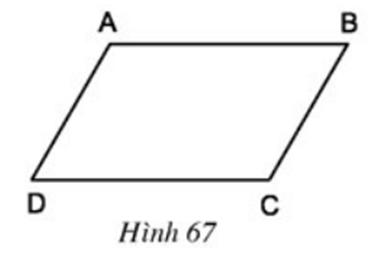
Lời giải

- Các cạnh đối bằng nhau

- Các góc đối bằng nhau

- Hai đường chéo cắt nhau tại trung điểm mỗi đường

Câu hỏi 3 trang 92 SGK Toán 8 tập 1

Trong các tứ giác ở hình 70, tứ giác nào là hình bình hành? Vì sao?

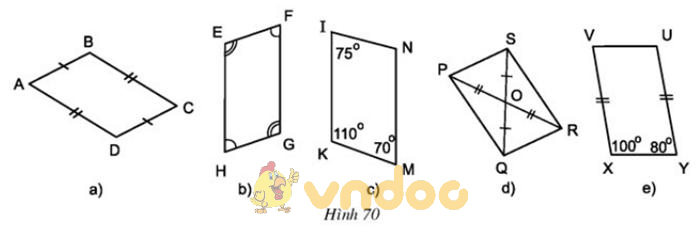
Lời giải

ABCD là hình bình hình vì có các cạnh đối bằng nhau

EFGH là hình bình hành vì có các góc đối bằng nhau

PQRS là hình bình hành vì có hai đường chéo cắt nhau tại trung điểm mỗi đường

XYUV là hình bình hành vì có XV = YU và XV // YU

Bài 43 trang 92 SGK Toán 8 Tập 1

Các tứ giác ABCD, EFGH, MNPQ trên giấy kẻ ô vuông ở hình 71 có là hình bình hành hay không?

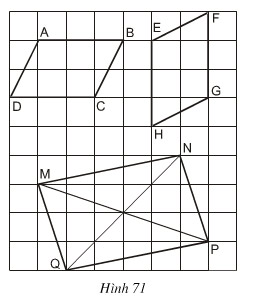
Lời giải:

Cả ba tứ giác là hình bình hành

- Tứ giác ABCD là hình bình hành vì có AB // CD và AB = CD = 3 (dấu hiệu nhận biết 3)

- Tứ giác EFGH là hình bình hành vì có EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)

- Tứ giác MNPQ là hình bình hành vì có MN = PQ và MQ = NP (dấu hiệu nhận biết 2)

(Chú ý:

- Với các tứ giác ABCD, EFGH còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 2.

- Với tứ giác MNPQ còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 5.)

Bài 44 trang 92 SGK Toán 8 Tập 1

Cho hình bình hành ABCD. Gọi E là trung điểm của AD, F là trung điểm của BC. Chứng minh rằng BE = DF

Lời giải:

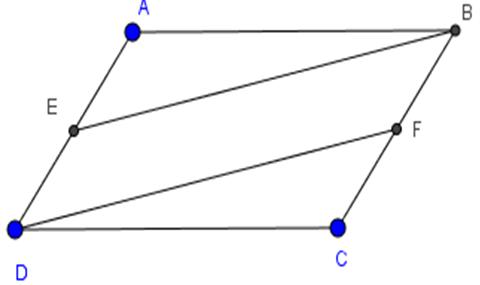
ABCD hình bình hành nên DE // BF và AD=BC

E là trung điểm của AD (giả thiết) nên \(DE = \dfrac{1}{2}AD\) (tính chất trung điểm)

F là trung điểm của BC (giả thiết) nên \(BF= \dfrac{1}{2}BC\) (tính chất trung điểm)

Mà AD=BC (chứng minh trên) nên DE=BF

Tứ giác BEDF có DE//BF và DE=BF (chứng minh trên)

⇒ Tứ giác BEDF là hình bình hành (theo dấu hiệu nhận biết hình bình hành).

⇒ BE = DF (tính chất hình bình hành).

Bài 45 trang 92 SGK Toán 8 Tập 1

Cho hình bình hành ABCD (AB > BC). Tia phân giác của góc D cắt AB ở E, tia phân giác của góc B cắt CD ở F.

a) Chứng minh rằng DE // BF

b) Tứ giác DEBF là hình gì? Vì sao?

Lời giải:

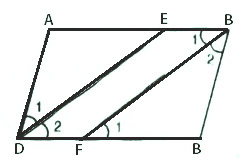
a) Vì ABCD là hình bình hành (giả thiết)

\(\Rightarrow \widehat {ABC} = \widehat {ADC}\) (tính chất hình bình hành) (1)

Vì BF là tia phân giác \(\widehat {ABC}\) (giả thiết)

\(\Rightarrow \widehat {{B_1}} = \widehat {{B_2}} = \dfrac{{\widehat {ABC}}}{2}\) (tính chất tia phân giác) (2)

Vì DE là tia phân giác \(\widehat {ADC}\) (giả thiết)

\(\Rightarrow \widehat {{D_1}} = \widehat {{D_2}} = \dfrac{{\widehat {ADC}}}{2}\) (tính chất tia phân giác) (3)

Từ (1), (2), (3) \(\Rightarrow \widehat {{D_2}} = \widehat {{B_1}}\) (4)

Có AB//DC (vì ABCD là hình bình hành)

Suy ra: \(\widehat {{B_1}} = \widehat {{F_1}}\) (so le trong) (5)

Từ (4) và (5) suy ra \(\widehat {{F_1}} = \widehat {{D_2}}\) mà hai góc này ở vị trí đồng vị nên DE//BF (dấu hiệu nhận biết hai đường thẳng song song)

b) ABCD là hình bình hành (giả thiết)

⇒ AB // CD (tính chất hình bình hành) hay BE // DF

Xét tứ giác DEBF có BE // DF (chứng minh trên) và DE//BF (theo câu a)

Suy ra tứ giác DEBF là hình bình hành (dấu hiệu nhận biết hình bình hành).

Bài 46 trang 92 SGK Toán 8 Tập 1

Các câu sau đúng hay sai?

a) Hình thang có hai cạnh đáy bằng nhau là hình bình hành

b) Hình thang có hai cạnh bên song song là hình bình hành

c) Tứ giác có hai cạnh đối bằng nhau là hình bình hành

d) Hình thang có hai cạnh bên bằng nhau là hình bình hành

Lời giải:

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5

b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)

c) Sai, vì hình thang cân có hai cạnh đối (hai cạnh bên) bằng nhau nhưng nó không phải là hình bình hành

d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

Bài 47 trang 93 SGK Toán 8 Tập 1

Cho hình 72. Trong đó ABCD là hình bình hành

a) Chứng minh rằng AHCK là hình bình hành

b) Gọi O là trung điểm của HK. Chứng minh rằng ba điểm A, O, C thẳng hàng.

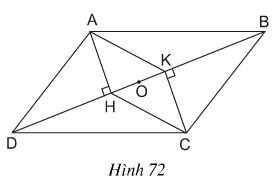
Lời giải:

a) Xét hai tam giác vuông AHD và CKB có:

+) AD = CB (vì ABCD là hình bình hành)

+) \(\widehat {ADH} = \widehat {CBK}\) (hai góc ở vị trí so le trong, AD//BC)

\(\Rightarrow ∆AHD = ∆CKB\) (cạnh huyền - góc nhọn)

\(\Rightarrow AH = CK\) (2 cạnh tương ứng)

Ta có:

\(\left\{ \begin{array}{l} AH \bot B{\rm{D}}\\ CK \bot B{\rm{D}} \end{array} \right.\left( \text{giả thiết} \right) \Rightarrow AH//CK\)

Xét tứ giác AHCK có:

\(\left\{ \begin{array}{l} AH//CK\\ AH = CK \end{array} \right.\left( \text{chứng minh trên} \right)\)

⇒ Tứ giác AHCK là hình bình hành (dấu hiệu nhận biết hình bình hành).

b) Xét hình bình hành AHCK có O là trung điểm của HK (giả thiết)

⇒ O là giao điểm của hai đường chéo AC và HK của hình bình hành (tính chất hình bình hành)

Hay A,O,C thẳng hàng.

Bài 48 trang 93 SGK Toán 8 Tập 1

Tứ giác ABCD có E, F, G, H theo thứ tự là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Lời giải:

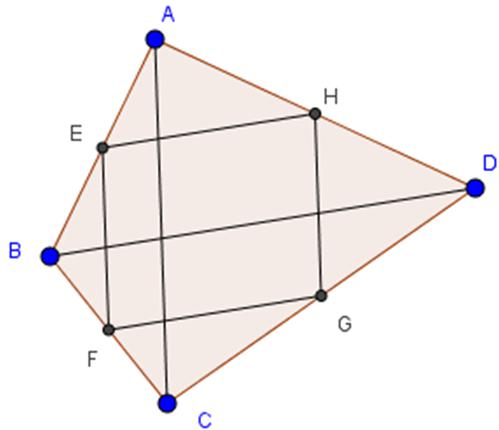
Tứ giác EFGH là hình bình hành

- Cách 1:

EB = EA, FB = FC (gt) nên EF là đường trung bình của ΔABC

Do đó EF // AC.

Tương tự HG là đường trung bình của ΔACD do đó HG // AC

Suy ra EF // HG (1)

Tương tự: EH // FG (2)

Từ (1) và (2) suy ra EFGH là hình bình hành (dấu hiệu nhận biết 1).

- Cách 2:

Suy ra EF = HG.

Lại có EF // HG (cmt)

Vậy EFGH là hình bình hành (dấu hiệu nhận biết 3)

Bài 49 trang 93 SGK Toán 8 Tập 1

Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:

a) AI // CK

b) DM = MN = NB

Lời giải:

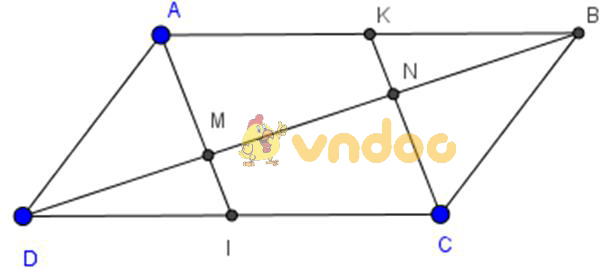
a)

Mà AB = CD (ABCD là hình bình hành).

=> AK = IC

Tứ giác AKCI có AK = CI, AK// CI nên AKCI là hình bình hành.

Do đó AI // CK

b) ΔDCN có DI = IC, IM // MN (vì AI // CK) nên suy ra DM = MN

Chứng minh tương tự đối với ΔABM ta có MN = NB.

Vậy DM = MN = NB (đpcm).

................................

Trên đây, VnDoc đã gửi tới các bạn tài liệu Giải Toán 8 bài 7: Hình bình hành. Để tham khảo lời giải những bài tiếp theo, mời các bạn vào chuyên mục Giải bài tập Toán lớp 8 trên VnDoc nhé. Chuyên mục tổng hợp lời giải Toán lớp 8 theo từng đơn vị bài học giúp các em nắm vững kiến thức được học trong từng bài, từ đó học tốt Toán 8 hơn.

Ngoài Soạn Toán 8, mời các bạn tham khảo thêm Giải bài tập Toán lớp 8, Giải vở bài tập Toán 8, soạn bài 8 hoặc đề thi học học kì 1 lớp 8, đề thi học học kì 2 lớp 8 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với Tài liệu học tập lớp 8 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tốt.

Bài tiếp theo: Giải Toán 8 bài 8: Đối xứng tâm