2.3: Graphs Of The Tangent And Cotangent Functions

Analyzing the Graph of \(y =\tan x\)

We will begin with the graph of the tangent function, plotting points as we did for the sine and cosine functions. Recall that

\[\tan \, x=\dfrac{\sin \, x}{\cos \, x}\]

The period of the tangent function is \(\pi\) because the graph repeats itself on intervals of \(k\pi\) where \(k\) is a constant. If we graph the tangent function on \(−\frac{\pi}{2}\) to \(\frac{\pi}{2}\), we can see the behavior of the graph on one complete cycle. If we look at any larger interval, we will see that the characteristics of the graph repeat.

We can determine whether tangent is an odd or even function by using the definition of tangent.

\[\begin{align*} \tan(-x)&= \dfrac{\sin(-x)}{\cos(-x)} \qquad \text{Definition of tangent}\\[4pt] &= \dfrac{-\sin \, x}{\cos \, x} \qquad \text{Sine is an odd function, cosine is even}\\[4pt] &= -\dfrac{\sin \, x}{\cos \, x} \qquad \text{The quotient of an odd and an even function is odd}\\[4pt] &= -\tan \, x \qquad \text{Definition of tangent} \end{align*}\]

Therefore, tangent is an odd function. We can further analyze the graphical behavior of the tangent function by looking at values for some of the special angles, as listed in Table \(\PageIndex{1}\).

Table \(\PageIndex{1}\)

\(x\)	\(−\dfrac{\pi}{2}\)	\(−\dfrac{\pi}{3}\)	\(−\dfrac{\pi}{4}\)	\(−\dfrac{\pi}{6}\)	0	\(\dfrac{\pi}{6}\)	\(\dfrac{\pi}{4}\)	\(\dfrac{\pi}{3}\)	\(\dfrac{\pi}{2}\)
\(\tan x\)	undefined	\(-\sqrt{3}\)	\(–1\)	\(-\dfrac{\sqrt{3}}{3}\)	0	\(\dfrac{\sqrt{3}}{3}\)	1	\(\sqrt{3}\)	undefined

These points will help us draw our graph, but we need to determine how the graph behaves where it is undefined. If we look more closely at values when \(\frac{\pi}{3}<x<\frac{\pi}{2}\), we can use a table to look for a trend. Because \(\frac{\pi}{3}≈1.05\) and \(\frac{\pi}{2}≈1.57\), we will evaluate \(x\) at radian measures \(1.05<x<1.57\) as shown in Table \(\PageIndex{2}\).

Table \(\PageIndex{2}\)

\(x\)	1.3	1.5	1.55	1.56
\(\tan x\)	3.6	14.1	48.1	92.6

As \(x\) approaches \(\dfrac{\pi}{2}\), the outputs of the function get larger and larger. Because \(y=\tan \, x\) is an odd function, we see the corresponding table of negative values in Table \(\PageIndex{3}\).

Table \(\PageIndex{3}\)

\(x\)	−1.3	−1.5	−1.55	−1.56
\(\tan x\)	−3.6	−14.1	−48.1	−92.6

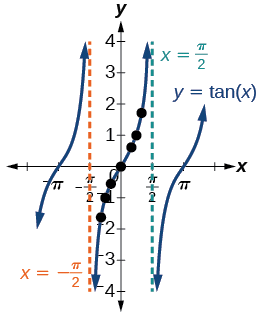
We can see that, as \(x\) approaches \(−\frac{\pi}{2}\), the outputs get smaller and smaller. Remember that there are some values of \(x\) for which \(\cos \, x=0\). For example, \(\cos \left (\frac{\pi}{2} \right)=0\) and \(\cos \left (\frac{3\pi}{2} \right )=0\). At these values, the tangent function is undefined, so the graph of \(y=\tan \, x\) has discontinuities at \(x=\frac{\pi}{2}\) and \(\frac{3\pi}{2}\). At these values, the graph of the tangent has vertical asymptotes. Figure \(\PageIndex{1}\) represents the graph of \(y=\tan \, x\). The tangent is positive from \(0\) to \(\frac{\pi}{2}\) and from \(\pi\) to \(\frac{3\pi}{2}\), corresponding to quadrants I and III of the unit circle.