2.6: Continuity - Mathematics LibreTexts

Continuity at a Point

Before we look at a formal definition of what it means for a function to be continuous at a point, let’s consider various functions that fail to meet our intuitive notion of what it means to be continuous at a point. We then create a list of conditions that prevent such failures.

Our first function of interest is shown in Figure. We see that the graph of \(f(x)\) has a hole at a. In fact, \(f(a)\) is undefined. At the very least, for \(f(x)\) to be continuous at a, we need the following condition:

i. \(f(a)\) is defined.

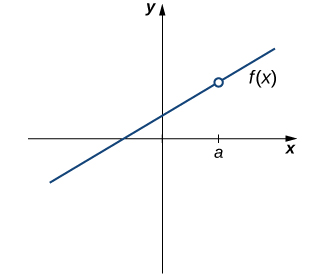
Figure \(\PageIndex{1}\): The function \(f(x)\) is not continuous at a because \(f(a)\) is undefined.

However, as we see in Figure, this condition alone is insufficient to guarantee continuity at the point a. Although \(f(a)\) is defined, the function has a gap at a. In this example, the gap exists because \(lim_{x→a}f(x)\) does not exist. We must add another condition for continuity at a—namely,

\[\lim_{x \to 2}h(x)=+∞.\]

ii. \(lim_{x→a}f(x)\) exists.

ii. \(lim_{x \to a}f(x)\) exists.

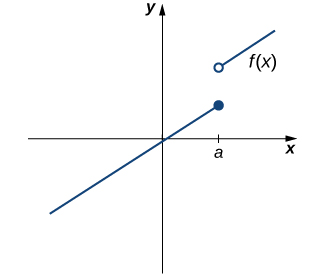
Figure \(\PageIndex{2}\): The function \(f(x)\) is not continuous at a because \(lim_{x→a}f(x)\) does not exist.

However, as we see in Figure, these two conditions by themselves do not guarantee continuity at a point. The function in this figure satisfies both of our first two conditions, but is still not continuous at a. We must add a third condition to our list:

iii. \(lim_{x→a}f(x)=f(a)\).

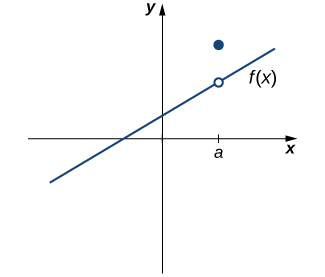
Figure \(\PageIndex{3}\): The function \(f(x)\) is not continuous at a because \(lim_{x→a}f(x)≠f(a)\).

Now we put our list of conditions together and form a definition of continuity at a point.

Definition

A function \(f(x)\) is continuous at a point a if and only if the following three conditions are satisfied:

1. \(f(a)\) is defined
2. \(lim_{x→a}f(x)\) exists
3. \(lim_{x→a}f(x)=f(a)\)

A function is discontinuous at a point a if it fails to be continuous at a.

The following procedure can be used to analyze the continuity of a function at a point using this definition.

Problem-Solving Strategy: Determining Continuity at a Point

1. Check to see if \(f(a)\) is defined. If \(f(a)\) is undefined, we need go no further. The function is not continuous at a. If \(f(a)\) is defined, continue to step 2.
2. Compute \(lim_{x→a}f(x)\). In some cases, we may need to do this by first computing \(lim_{x→a^−}f(x)\) and \(lim_{x→a^+}f(x)\). If \(lim_{x→a}f(x)\) does not exist (that is, it is not a real number), then the function is not continuous at a and the problem is solved. If \(lim_{x→a}f(x)\) exists, then continue to step 3.
3. Compare \(f(a)\) and \(lim_{x→a}f(x)\). If \(lim_{x→a}f(x)≠f(a)\), then the function is not continuous at a. If \(lim_{x→a}f(x)=f(a)\), then the function is continuous at a.

The next three examples demonstrate how to apply this definition to determine whether a function is continuous at a given point. These examples illustrate situations in which each of the conditions for continuity in the definition succeed or fail.

Example \(\PageIndex{1A}\): Determining Continuity at a Point, Condition 1

Using the definition, determine whether the function \(f(x)=(x^2−4)/(x−2)\) is continuous at \(x=2\). Justify the conclusion.

Solution

Let’s begin by trying to calculate \(f(2)\). We can see that \(f(2)=0/0\), which is undefined. Therefore, \(f(x)=\frac{x^2−4}{x−2}\) is discontinuous at 2 because \(f(2)\) is undefined. The graph of \(f(x)\) is shown in Figure.

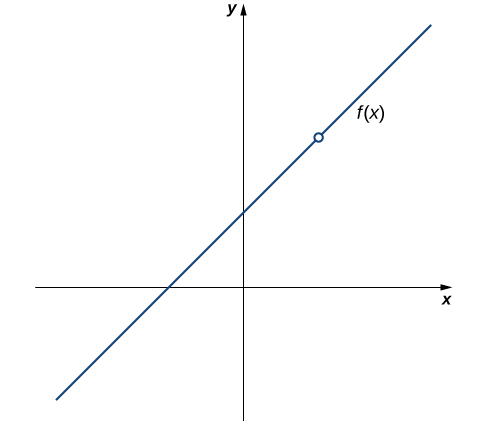
Figure \(\PageIndex{4}\): The function \(f(x)\) is discontinuous at 2 because \(f(2)\) is undefined.

Example \(\PageIndex{1B}\): Determining Continuity at a Point, Condition 2

Using the definition, determine whether the function \(f(x)=\begin{cases}−x^2+4 & if x≤3 \\ 4x−8 & if x>3\end{cases}\) is continuous at \(x=3\). Justify the conclusion.

Solution

Let’s begin by trying to calculate \(f(3)\).

\(f(3)=−(3^2)+4=−5\).

Thus, \(f(3)\) is defined. Next, we calculate \(lim_{x→3}f(x)\). To do this, we must compute \(lim_{x→3^−}f(x)\) and \(lim_{x→3^+}f(x)\):

\(lim_{x→3^−}f(x)=−(3^2)+4=−5\)

and

\(lim_{x→3^+}f(x)=4(3)−8=4\).

Therefore, \(lim_{x→3}f(x)\) does not exist. Thus, \(f(x)\) is not continuous at 3. The graph of \(f(x)\) is shown in Figure.

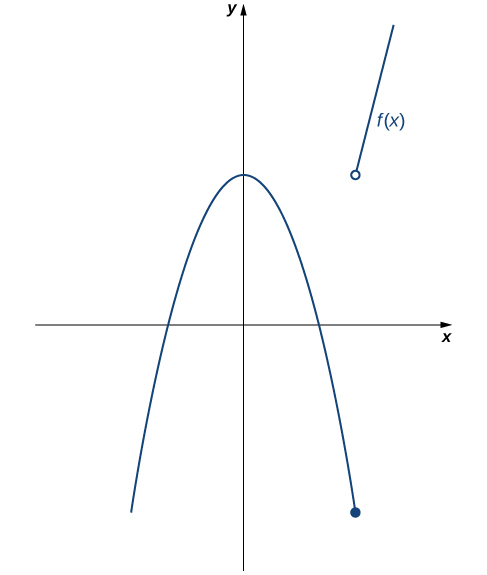
Figure \(\PageIndex{5}\): The function \(f(x)\) is not continuous at 3 because \(lim_{x→3}f(x)\) does not exist.

Example \(\PageIndex{1C}\): Determining Continuity at a Point, Condition 3

Using the definition, determine whether the function \(f(x)=\begin{cases}\frac{sinx}{x} & if x≠0\\1 & if x=0\end{cases}\) is continuous at x=0.

Solution

First, observe that

\(f(0)=1\)

Next,

\(lim_{x→0}f(x)=lim_{x→0}\frac{sinx}{x}=1\).

Last, compare \(f(0)\) and \(lim_{x→1}f(x)\). We see that

\(f(0)=1=lim_{x→0}f(x)\).

Since all three of the conditions in the definition of continuity are satisfied, \(f(x)\) is continuous at \(x=0\).

Exercise \(\PageIndex{1}\)

Using the definition, determine whether the function \(f(x)=\begin{cases}2x+1 & if x<1\\2 & if x=1\\ −x+4 & if x>1\end{cases}\) is continuous at \(x=1\). If the function is not continuous at 1, indicate the condition for continuity at a point that fails to hold.

Hint

Check each condition of the definition.

Answer

f is not continuous at 1 because \(f(1)=2≠3=lim_{x→1}f(x)\).

By applying the definition of continuity and previously established theorems concerning the evaluation of limits, we can state the following theorem.

Continuity of Polynomials and Rational Functions

Polynomials and rational functions are continuous at every point in their domains.

Proof

Previously, we showed that if \(p(x)\) and \(q(x)\) are polynomials, \(lim_{x→a}p(x)=p(a)\) for every polynomial \(p(x)\) and \(lim_{x→a}\frac{p(x)}{q(x)}=\frac{p(a)}{q(a)}\) as long as \(q(a)≠0\). Therefore, polynomials and rational functions are continuous on their domains.

□

We now apply Note to determine the points at which a given rational function is continuous.

Example \(\PageIndex{2}\):Continuity of a Rational Function

For what values of x is \(f(x)=\frac{x+1}{x−5}\) continuous?

Solution

The rational function \(f(x)=\frac{x+1}{x−5}\) is continuous for every value of x except \(x=5\).

Exercise \(\PageIndex{2}\)

For what values of x is \(f(x)=3x^4−4x^2\) continuous?

Hint

Use Note

Answer

\(f(x)\) is continuous at every real number.