2.6: The SSS Theorem - Mathematics LibreTexts

Skip to main content

1. Theorem \(\PageIndex{1}\): Side-Side-Side (SSS) Theorem
2. Example \(\PageIndex{1}\)
3. Proof of Theorem \(\PageIndex{1}\)
4. Example \(\PageIndex{2}\)
5. Application: Triangular Bracing
6. Problems

We now consider the case where the side of two triangles are known to be of the same length.

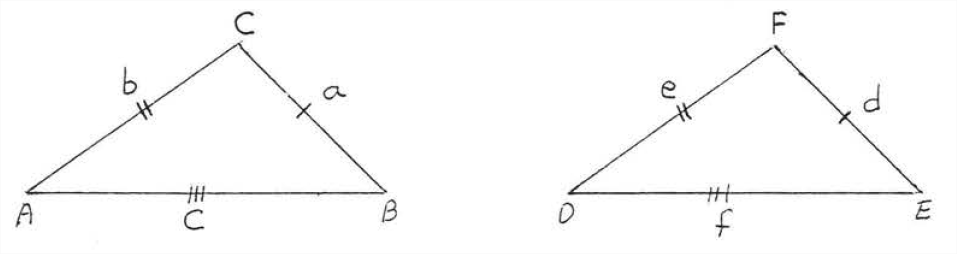
Theorem \(\PageIndex{1}\): Side-Side-Side (SSS) Theorem

Two triangles are congruent if three sides of one are equal respectively to three sides of the other (\(SSS = SSS\)).

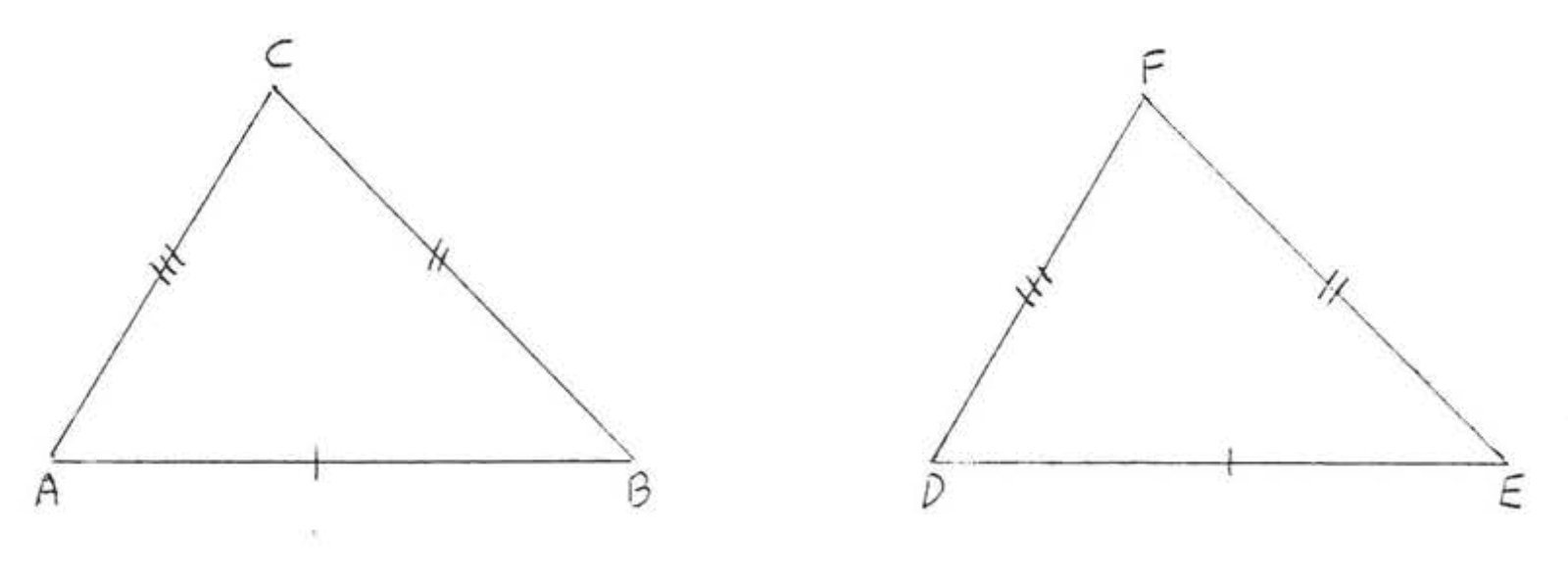
Theorem \(\PageIndex{1}\) is demonstrated in Figure \(\PageIndex{1}\): if \(a=d, b=e,\) and \(c=f\) then \(\triangle ABC \cong \triangle DEF\)

Example \(\PageIndex{1}\)

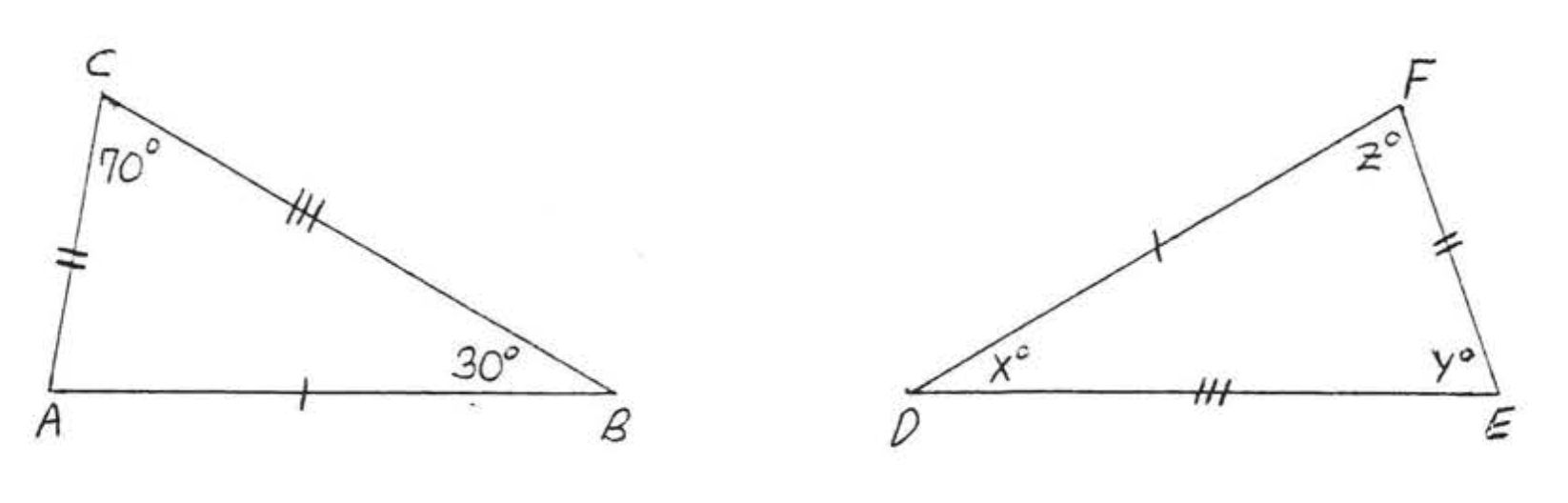
Find \(x, y, z:\)

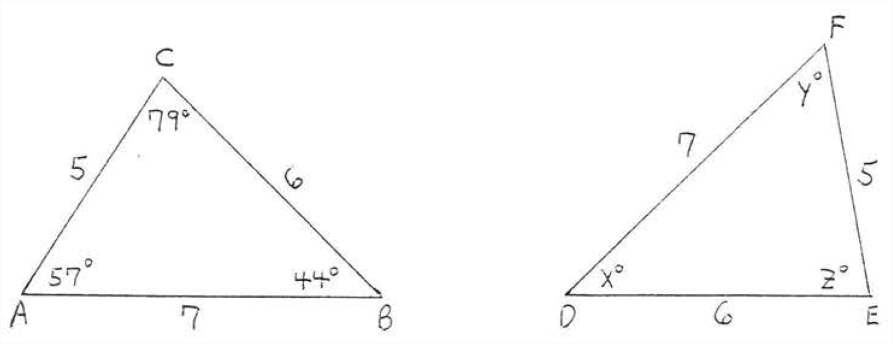
Solution

\(AB = 7 = DF\). Therefore \(\angle C,\) the angle opposite AB must correspond to \(\angle E\), the angle opposite \(DF\). In the same way \(\angle A\) corresponds to \(\angle F\) and \(\angle B\) corresponds to \(\angle D\). We have \(\triangle ABC \cong \triangle FDE\) by \(SSS = SSS\), so

\(x^{\circ}=\angle D=\angle B=44^{\circ}\)

\(y^{\circ}=\angle F=\angle A=57^{\circ}\)

\(z^{\circ}=\angle E=\angle C=79^{\circ}\)

Answer: \(x = 44, y=57, z=79\)

Proof of Theorem \(\PageIndex{1}\)

In Figure \(\PageIndex{1}\), place \(\triangle ABC\) and \(\triangle DEF\) so that their longest sides coincide, in this case \(AB\) and \(DE\). This can be done because \(AB = c= r = DE.\) Now draw \(CF\), forming angles \(1,2,3,\) and 4 (Figure \(\PageIndex{2}\)). The rest of the proof will be presented in double-column form:

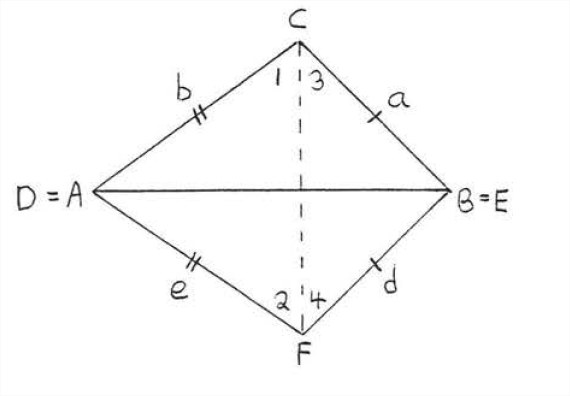
Statement	Reasons
1. \(\angle 1 = \angle 2\).	1. The base angles of isosceles triangle \(CAF\) are equal (Theorem \(\PageIndex{1}\), section 2.5).
2. \(\angle 3 = \angle 4\).	2. The base angles of isosceles triangle \(CBF\) are equal.
3. \(\angle C = \angle F\).	3. \(\angle C = \angle 1 + \angle 3 = \angle 2 + \angle 4 = \angle F\).
4. \(AC = DF\).	4. Given, \(AC = b = e = DF\).
5. \(BC = EF\).	5. Given, \(BC = a = d = EF\).
6. \(\triangle ABC \cong \triangle DEF\).	6. \(SAS = SAS\): \(AC, \angle C, BC\) of \(\triangle ABC = DF\), \(\angle F\), \(EF\) of \(\triangle DEF\).

Example \(\PageIndex{2}\)

Given \(AB = DE, BC = EF,\) and \(AC = DF\). Prove \(\angle C = \angle F\)

Solution

Statements	Reasons
1. \(AB = DE\).	1. Given.
2. \(BC = EF\).	2. Given.
3. \(AC = DF\).	3. Given.
4. \(\triangle ABC \cong \triangle DEF\).	4. \(SSS = SSS\): \(AB, BC, AC\) of \(\triangle ABC = DE\), \(EF, DF\) of \(\triangle DEF\).
5. \(\angle C = \angle F\).	5. Corresponding angles of congruent triangles are equal.

Application: Triangular Bracing

The SSS Theorem is the basis of an important principle of construction engineering called triangular bracing. Imagine the line segments in Figure \(\PageIndex{3}\) to be beans of wood or steel joined at the endpoints by nails or screws. If pressure is applied to one of the sides, \(ABCD\) will collapse and look like \(A'B'C'D'\).

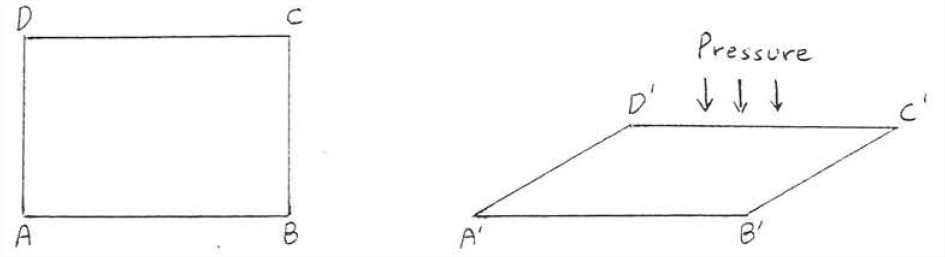
Now suppose points \(A\) and \(C\) are joined by a new beam, called a brace (Figure \(\PageIndex{4}\)). The structure will not collapse as long as the beans remain unbroken and joined together. It is impossible to deform \(ABCD\) into any other shape \(A'B'C'D'\) because if \(AB = A'B'\), \(BC = B'C'\), and \(AC = A'C'\) then \(\triangle ABC\) would be congruent to \(\triangle A'B'C'\) by \(SSS = SSS\).

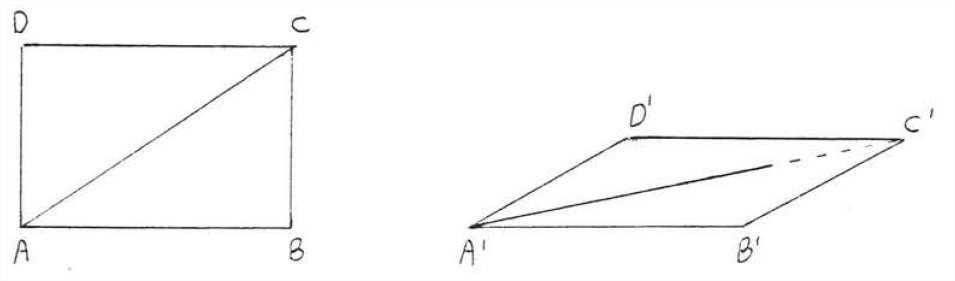
We sometimes say that a triangle is a rigid figure; once the sides of a triangle are fixed the angles cannot be changed. Thus in Figure \(\PageIndex{4}\), the shape of \(\triangle ABC\) cannot be changed as long as the lengths of its sides remain the same.

Problems

1 - 8. For each of the following (1) write the congruence statement,

(2) given the reason for (1) (\(SAS\), \(ASA\), \(AAS\), or \(SSS\) Theorem), and

(3) find \(x\), or \(x\) and \(y\), or \(x, y\), and \(z\).

1.

2.

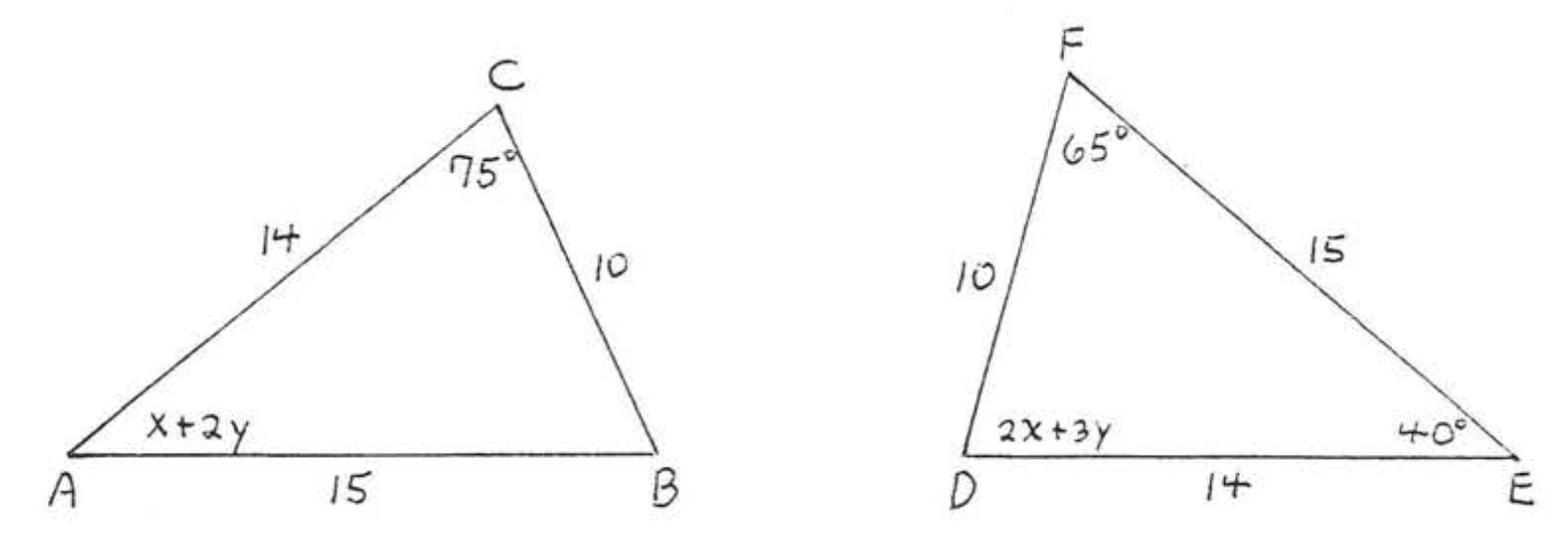
3.

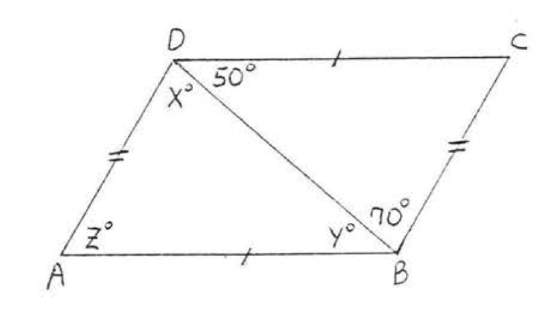
4.

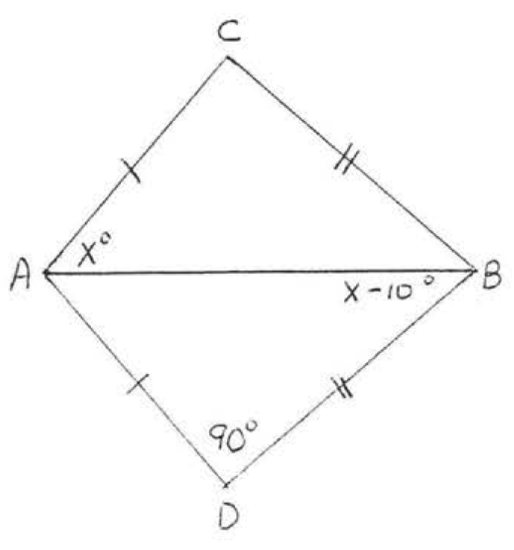
5.

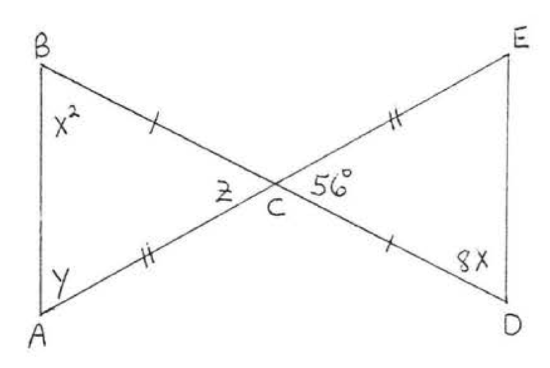
6.

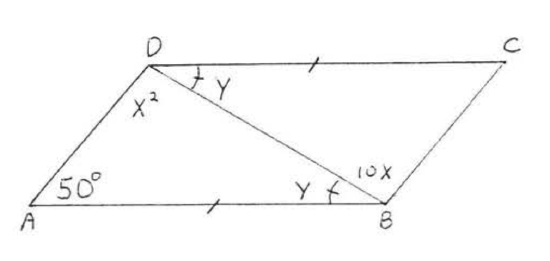
7.

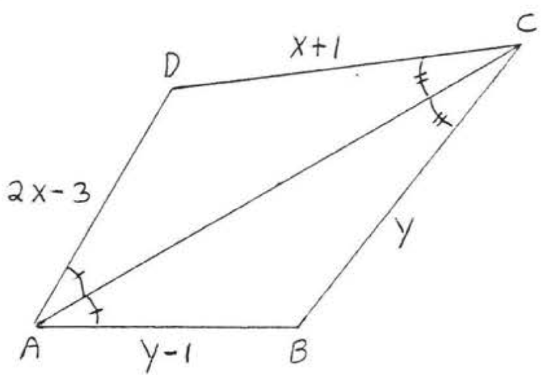
8.

9. Given \(AB = DE\), \(BC = EF\), and \(AC = DF\). Prove \(\angle A = \angle D\).

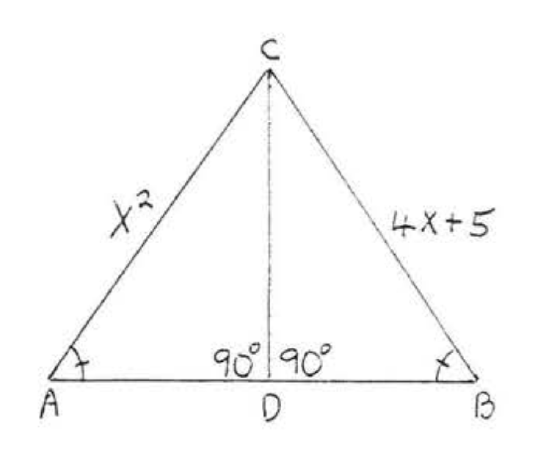
10. Given \(AC = BC\). \(AD = BD\). Prove \(\angle ADC = \angle BDC\).

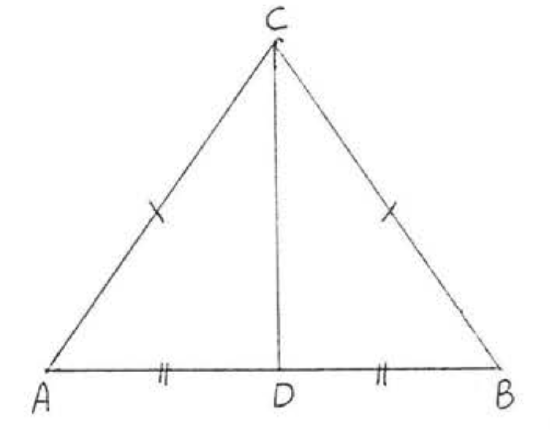
11. Given \(AB = AD\), \(BC = DC\). Prove \(\angle BAC = \angle CAD\).

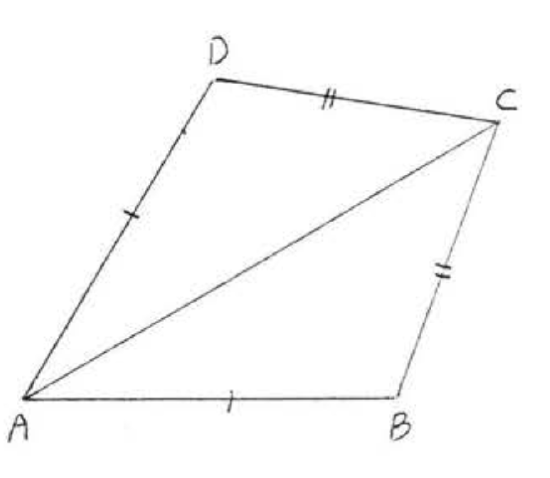
12. Given \(AB = CD\), \(BC = DA\). Prove \(\angle BAC = \angle DCA\).

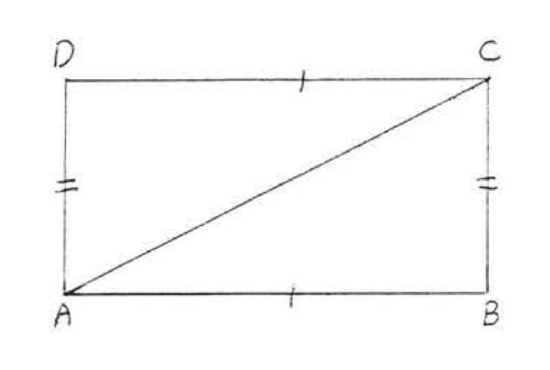
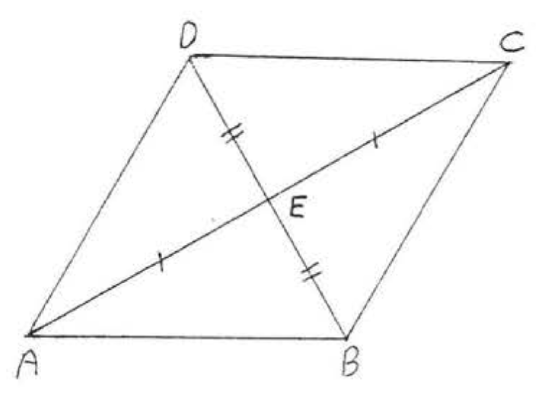
13. Given \(AE = CE\), \(BE = ED\). Prove \(AB = CD\).

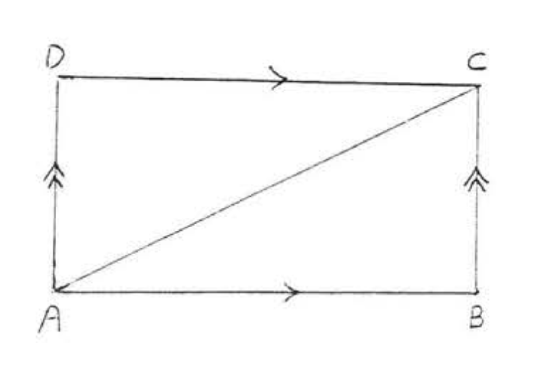
14. Given \(AB||CD\), \(AD||BC\). Prove \(AB = CD\).