3.4: Graphs Of Polynomial Functions - Mathematics LibreTexts

Identify Zeros and Their Multiplicities from a Graph

Graphs behave differently at various \(x\)-intercepts. Sometimes, the graph will cross over the horizontal axis at an intercept. Other times, the graph will touch the horizontal axis and bounce off. Suppose, for example, we graph the function

\[f(x)=(x+3)(x−2)^2(x+1)^3 \nonumber\]

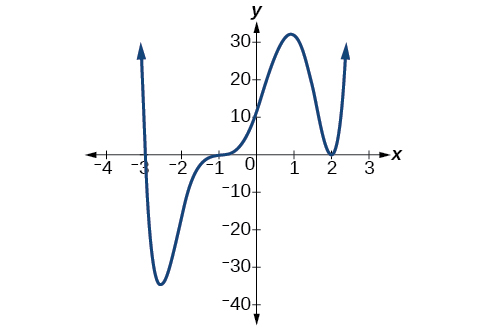Notice in the figure to the right illustrates that the behavior of this function at each of the \(x\)-intercepts is different.

The \(x\)-intercept −3 is the solution of equation \((x+3)=0\). The graph passes directly through the \(x\)-intercept at \(x=−3\). The factor is linear (has a degree of 1), so the behavior near the intercept is like that of a line—it passes directly through the intercept. We call this a single zero because the zero corresponds to a single factor of the function.

The \(x\)-intercept 2 is the repeated solution of equation \((x−2)^2=0\). The graph touches the axis at the intercept and changes direction. The factor is quadratic (degree 2), so the behavior near the intercept is like that of a quadratic—it bounces off of the horizontal axis at the intercept. The factor is repeated, that is, \((x−2)^2=(x−2)(x−2)\), so the solution, \(x=2\), appears twice. The number of times a given factor appears in the factored form of the equation of a polynomial is called the multiplicity. The zero associated with this factor, \(x=2\), has multiplicity 2 because the factor \((x−2)\) occurs twice.

The \(x\)-intercept −1 is the repeated solution of factor \((x+1)^3=0\). The graph passes through the axis at the intercept, but flattens out a bit first. This factor is cubic (degree 3), so the behavior near the intercept is like that of a cubic—with the same S-shape near the intercept as the toolkit function \(f(x)=x^3\). We call this a triple zero, or a zero with multiplicity 3.

Graphical Behavior of Polynomials at \(x\)-intercepts

If a polynomial contains a factor of the form \((x−h)^p\), the behavior near the \(x\)-intercept is determined by the power \(p\). We say that \(x=h\) is a zero of multiplicity \(p\).

• The graph of a polynomial function will touch the \(x\)-axis at zeros with even multiplicities.
• The graph will cross the \(x\)-axis at zeros with odd multiplicities.
• The higher the multiplicity, the flatter the curve is at the zero.
• The sum of the multiplicities is the degree of the polynomial function.

For zeros with even multiplicities, the graphs touch or are tangent to the \(x\)-axis. For zeros with odd multiplicities, the graphs cross or intersect the \(x\)-axis. See the figure below for examples of graphs of polynomial functions with a zero of multiplicity 1, 2, and 3. The graphs clearly show that the higher the multiplicity, the flatter the graph is at the zero.

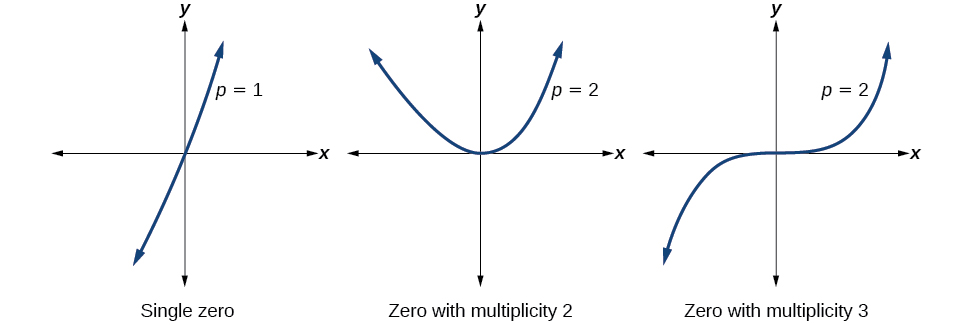
For higher even powers, such as 4, 6, and 8, the graph will still touch and bounce off of the horizontal axis but, for each increasing even power, the graph will appear flatter as it approaches and leaves the \(x\)-axis. For higher odd powers, such as 5, 7, and 9, the graph will still cross through the horizontal axis, but for each increasing odd power, the graph will appear flatter as it approaches and leaves the \(x\)-axis.

How to: Given a graph of a polynomial function, identify the zeros and their mulitplicities

1. If the graph crosses the \(x\)-axis at a zero, it is a zero with odd multiplicity.
2. If the graph touches and bounces off of the \(x\)-axis, it is a zero with even multiplicity.
3. The higher the multiplicity of the zero, the flatter the graph gets at the zero.

Example \(\PageIndex{1}\): Find Zeros and Their Multiplicities From a Graph

Use the graph of the function of degree 6 in the figure below to identify the zeros of the function and their possible multiplicities.

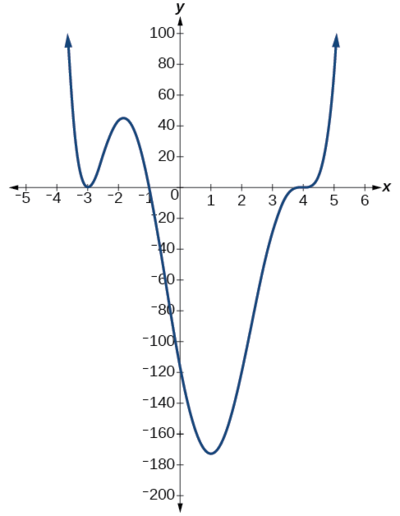Solution Starting from the left, the first zero occurs at \(x=−3\). The graph touches the \(x\)-axis, so the multiplicity of the zero must be even. The zero of −3 has multiplicity 2. The next zero occurs at \(x=−1\). The graph looks almost linear at this point. This is a single zero of multiplicity 1. The last zero occurs at \(x=4\). The graph crosses the \(x\)-axis, so the multiplicity of the zero must be odd. Since the graph is flat around this zero, the multiplicity is likely 3 (rather than 1). The polynomial function is of degree \(6\) so the sum of the multiplicities must be at least \(2+1+3\) or \(6\).

Try It \(\PageIndex{2}\)

Use the graph of the function in the figure below to identify the zeros of the function and their possible multiplicities.

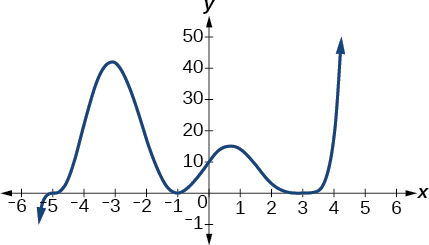
Graph of a polynomial function.

Answer

The zero at -5 is odd. Since the curve is somewhat flat at -5, the zero likely has a multiplicity of 3 rather than 1. The zero at -1 has even multiplicity of 2. The zero at 3 has even multiplicity. Since the curve is flatter at 3 than at -1, the zero more likely has a multiplicity of 4 rather than 2.