3.4: Graphs Of Polynomial Functions - Mathematics LibreTexts

Home » How To Graph A Polynomial Function » 3.4: Graphs Of Polynomial Functions - Mathematics LibreTexts

Maybe your like

Example \(\PageIndex{16}\): Writing a Formula for a Polynomial Function from the Graph

Construct the factored form of a possible equation for each graph given below.

(a)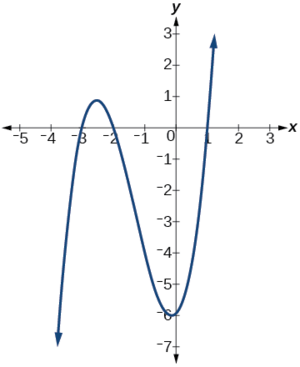
Graph of h(x)=x^3+4x^2+x-6.
Figure \(\PageIndex{16a}\): Graph of \(h(x)\).

Solution

Looking at the graph of this function, as shown in Figure \(\PageIndex{16}\), it appears that there are \(x\)-intercepts at \(x=−3,−2, \text{ and }1\).

Each \(x\)-intercept corresponds to a zero of the polynomial function and each zero yields a factor, so we can now write the polynomial in factored form.

\( h(x)=a(x+3)(x+2)(x−1) \)

The stretch factor \(a\) can be found by using another point on the graph, like the \(y\)-intercept, \((0,-6)\).

\[\begin{align*} f(0)&=a(0+3)(0+2)(0−1) \\ −6&=a(-6) \\ a&=1 \end{align*}\]

Thus \( h(x)=(x+3)(x+2)(x−1). \)

(b)

Graph of a positive even-degree polynomial with zeros at x=-3, 2, 5 and y=-2.
Figure \(\PageIndex{16b}\).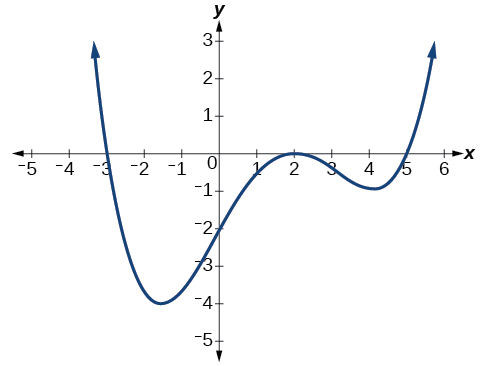

Solution

This graph has three \(x\)-intercepts: \(x=−3,\;2,\text{ and }5\). The \(y\)-intercept is located at \((0,2).\) At \(x=−3\) and \( x=5\), the graph passes through the axis linearly, suggesting the corresponding factors of the polynomial will be linear. At \(x=2\), the graph bounces at the intercept, suggesting the corresponding factor of the polynomial will be second degree (quadratic). Together, this gives us

\[f(x)=a(x+3)(x−2)^2(x−5)\]

To determine the stretch factor, we utilize another point on the graph. We will use the \(y\)-intercept \((0,–2)\), to solve for \(a\).

\[\begin{align*} f(0)&=a(0+3)(0−2)^2(0−5) \\ −2&=a(0+3)(0−2)^2(0−5) \\ −2&=−60a \\ a&=\dfrac{1}{30} \end{align*}\]

The graphed polynomial appears to represent the function \(f(x)=\dfrac{1}{30}(x+3)(x−2)^2(x−5)\).

Tag » How To Graph A Polynomial Function