30-60-90 Triangle - Rules, Formula, Theorem, Sides, Examples

30-60-90 Triangle

A 30-60-90 triangle is a special right-angled triangle as the angles of the triangle are in the ratio 1:2:3. There are different types of triangles such as obtuse, isosceles, acute, equilateral, and so on. But only a few types of triangles are considered special triangles. These triangles are special as their sides and angles are consistent and predictable. Their properties can be used to solve various geometry or trigonometry problems. A 30-60-90 triangle—pronounced "thirty sixty ninety"—is one such very special type of triangle indeed.

In this lesson, we will explore the concept of the 30-60-90 triangle and learn all about it including its formula, definition, sides, area, and the rules that apply to this triangle.

1.	What is 0-60-90 Triangle?
2.	30-60-90 Triangle Sides
3.	30-60-90-Triangle Theorem
4.	30-60-90 Triangle Proof
5.	30-60-90 Triangle Rule
6.	Area of a 30-60-90 Triangle
7.	FAQS on 30-60-90 Triangle

What is 30-60-90 Triangle?

The 30-60-90 triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 1:2:3. Here, a right triangle means being any triangle that contains a 90° angle. A 30-60-90 triangle is a special right triangle that always has angles of measure 30°, 60°, and 90°. Here are some of the variants of a 30-60-90 triangle. The triangles ABC and PQK are 30-60-90 triangles.

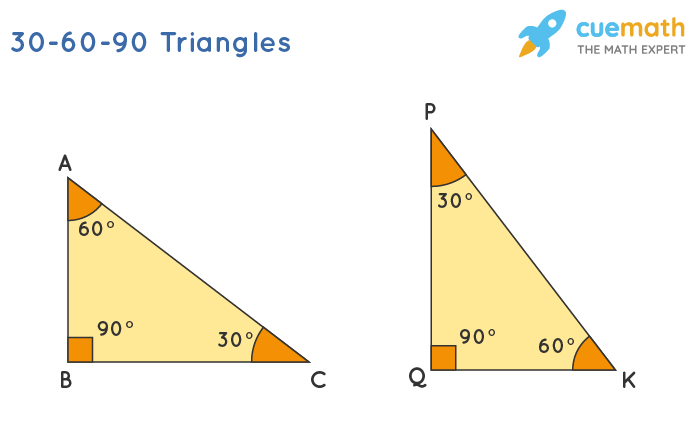
Here, in the triangle ABC, ∠ C = 30°,∠ A = 60°, and ∠ B = 90° and in the triangle PQK, ∠ P = 30°,∠ K = 60°, and ∠ Q = 90°

30-60-90 Triangle Sides

A 30-60-90 triangle is a special triangle since the length of its sides is always in a consistent relationship with one another.

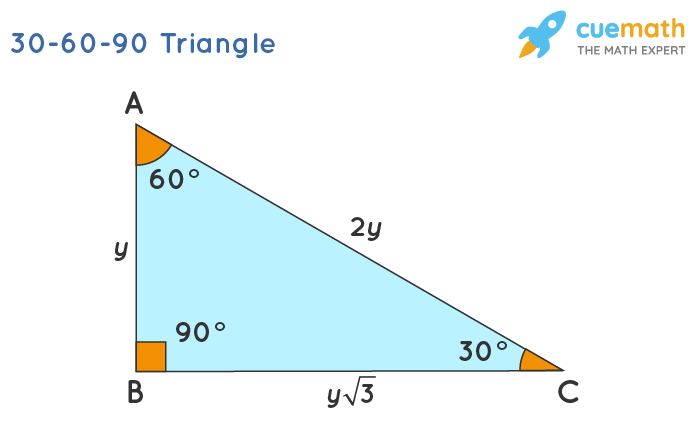
In the below-given 30-60-90 triangle ABC, ∠ C = 30°,∠ A = 60°, and ∠ B = 90°. We can understand the relationship between each of the sides from the below definitions:

• The side that is opposite to the 30° angle, AB = y will always be the smallest since 30° is the smallest angle in this triangle
• The side that is opposite to the 60° angle, BC = y × √3 = y√3 will be the medium length because 60° is the mid-sized degree angle in this triangle
• On the side that is opposite to the 90° angle, the hypotenuse AC = 2y will be the largest side because 90° is the largest angle.

The sides of a 30-60-90 triangle are always in the ratio of 1:√3: 2. This is also known as the 30-60-90 triangle formula for sides y: y√3: 2y. Let us learn the derivation of thisratio in the 30-60-90 triangle proof section. This formula can be verified using the Pythagoras theorem.

Consider some of the examples of a 30-60-90 degree triangle with these side lengths:

Here, in the 30-60-90 triangle DEF ∠ F = 30°,∠ D = 60°, and ∠ E = 90° The side opposite to the 30° angle, DE = y = 2 The side opposite to the 60° angle, BC = y√3 = 2√3 The side opposite to the 90° angle, the hypotenuse AC = 2y = 2 × 2 = 4	Here, in the 30-60-90 triangle PQR ∠ R = 30°,∠ P = 60°, and ∠ Q = 90° The side opposite to the 30° angle, AB = y = 7 The side opposite to the 60° angle, BC = y√3 = 7√3 The side opposite to the 90° angle, the hypotenuse AC = 2y = 2 × 7 = 14

30-60-90-Triangle Theorem

The statement of the 30-60-90-Triangle Theorem is given as,

Statement: The length of the hypotenuse is twice the length of the shortest side and the length of the other side is √3 times the length of the shortest side in a 30-60-90-Triangle.

30-60-90-Triangle Formula

The above theorem can be written mathematically as the 30-60-90-Triangle Formula as 1:√3: 2 which is the ratio of the three sides of the 30-60-90-Triangle. Another formula for this special triangle 1:2:3 which is the ratio of the three angles of the 30-60-90-Triangle​​​​​​.

30-60-90-Triangle Proof

Let's consider an equilateral triangle ABC with a side length equal to 'a'.

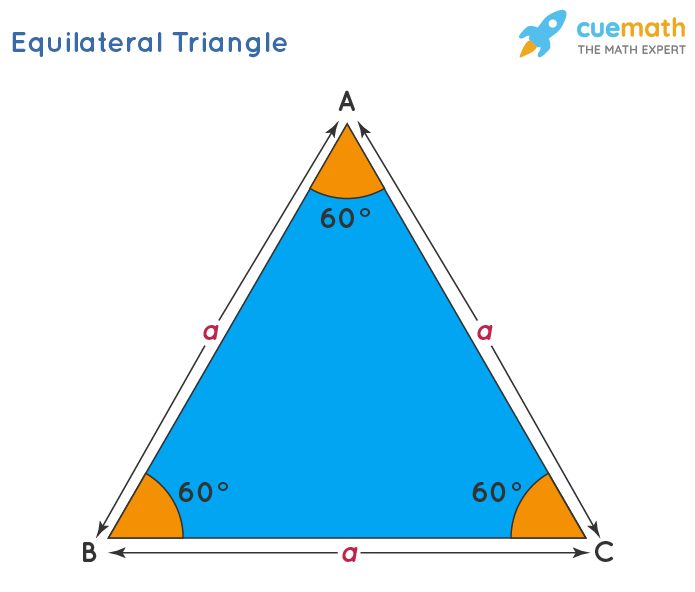
Now, draw a perpendicular from vertex A to side BC at point D of the triangle ABC. The perpendicular in an equilateral triangle bisects the other side.

Triangle ABD and ADC are two 30-60-90 triangles. Both the triangles are similar and right-angled triangles. Hence, we can apply the Pythagoras theorem to find the length AD.

(AB)2 = (AD)2 + (BD)2

a2 = (AD)2 + (a/2)2

a2 - (a/2)2 = (AD)2

3a2/4 = (AD)2

(a√3)/2 = AD

AD = (a√3)/2

BD = a/2

AB = a

These sides also follow the same ratio a/2 : (a√3)/2: a

Multiply by 2 and divide by 'a',

(2a)/(2a) : (2a√3)/(2a): (2a/a)

We get 1:√3:2. This is the 30-60-90 triangle theorem.

30-60-90 Triangle Rule

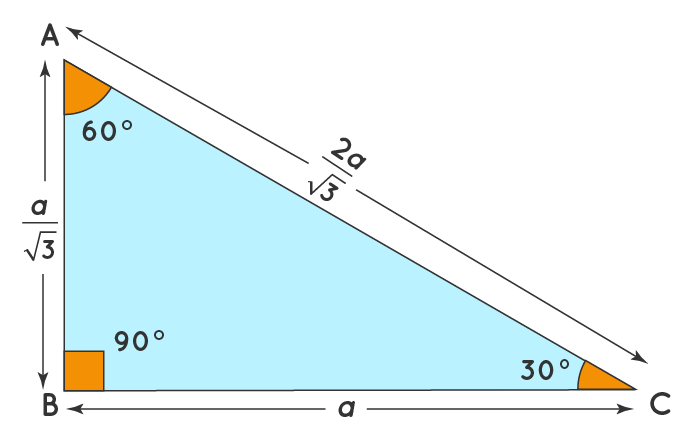
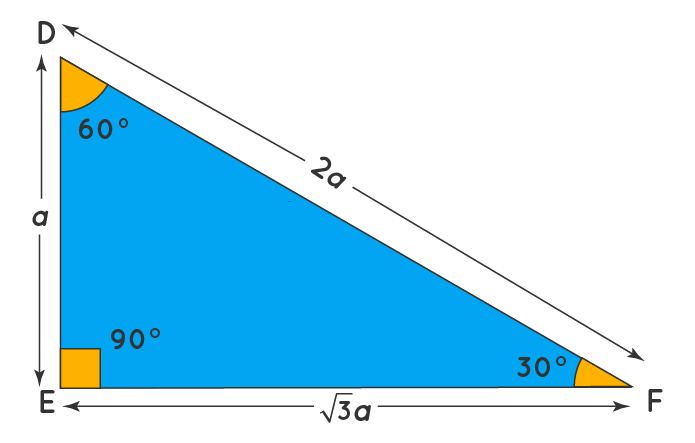
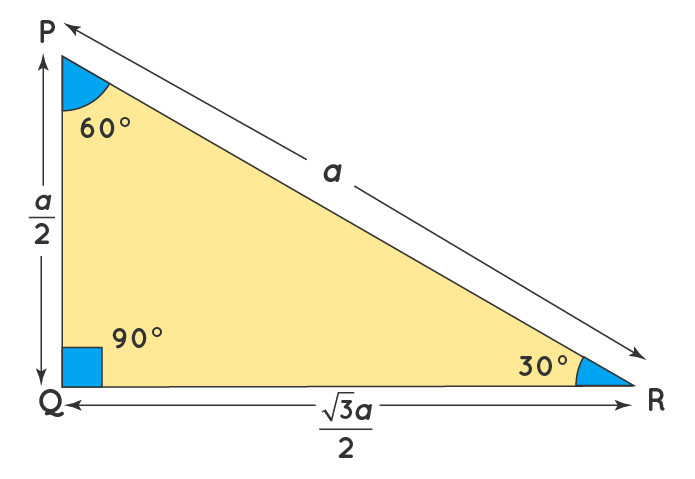
In a 30-60-90 triangle, the measure of any of the three sides can be found out by knowing the measure of at least one side in the triangle. This is called the 30-60-90 triangle rule. The below-given table shows how to find the sides of a 30-60-90 triangle using the 30-60-90 triangle rule:

Base is given	Perpendicular is given	Hypotenuse is given
The Base BC of the triangle is assumed to be 'a'.	The perpendicular DE of the triangle is assumed to be 'a'.	The hypotenuse PR of the triangle is assumed to be 'a'.
The perpendicular of the triangle ABC is AB = (a /√3) The hypotenuse of the triangle ABC is AC = (2a)/√3	The base of the triangle DEF is EF = √3a. The hypotenuse of the triangle DEF is DF = 2a.	The base of the triangle PQR is QR = (√3a)/2. The perpendicular of the triangle PQR is PQ = (a/2).

Area of a 30-60-90 Triangle

The formula to calculate the area of a triangle is = (1/2) × base × height. In a right-angled triangle, the height is the perpendicular of the triangle. Thus, the formula to calculate the area of a right-angle triangle is = (1/2) × base × perpendicular

Let's learn how to apply this formula to find the area of the 30-60-90 triangle.

Base BC of the triangle is assumed to be 'a', and the hypotenuse of the triangle ABC is AC. We have learned in the previous section how to find the hypotenuse when the base is given.

Let's apply the formula we have learned.

Thus, perpendicular of the triangle = a/√3

Area of the triangle = (1/2) × base × perpendicular

Area = 1/2 × a × a/√3

Therefore, the area of the 30-60-90 triangle when the base (side of middle length) is given as 'a' is: a2/(2√3)

Related Articles

• Triangles
• Isosceles Triangles
• Obtuse Triangles
• Acute Triangle
• Perimeter of a Triangle

Important Notes on 30-60-90 Triangle

Here is a list of a few points that should be remembered while studying 30-60-90 triangles:

• The 30-60-90 triangle is called a special right triangle as the angles of this triangle are in a unique ratio of 1:2:3 and the sides are in the ratio 1:√3: 2
• A 30-60-90 triangle is a special right triangle that always has angles of measure 30°, 60°, and 90°
• All the sides of a 30-60-90 triangle can be calculated if any one side is given. This is called the 30-60-90 triangle rule.