Additive Inverse - Property, Definition, Formula, Examples - Cuemath

Additive Inverse

Additive inverse is the number that is added to a given number to make the sum zero. For example, if we take the number 3 and add -3 to it, the result is zero. Hence, the additive inverse of 3 is -3. We come across such situations in our daily life where we nullify the value of a quantity by taking its additive inverse. Let us learn the additive inverse property of real and complex numbers in this article.

1.	What is Additive Inverse?
2.	Additive Inverse Property
3.	Additive Inverse Formula
4.	Additive Inverse and Multiplicative Inverse
5.	Additive Inverse in Algebraic Expressions
6.	FAQs on Additive Inverse

What is Additive Inverse?

The additive inverse of a number is its opposite number. If a number is added to its additive inverse, the sum of both the numbers becomes zero. The simple rule is to change the positive number to a negative number and vice versa. We know that, 7+ (-7) =0. Thus -7 is the additive inverse of 7 and 7 is the additive inverse of -7.

Additive Inverse Property

When the sum of two real numbers is zero, then each real number is said to be the additive inverse of the other. So, we have R + (-R) = 0, where R is a real number. R and -R are the additive inverses of each other. For example: 3/4 + (-3/4) = 0. Here 3/4 is the additive inverse of -3/4 and vice-versa. This is an example of the additive inverse of a fraction.

Let’s say you have a bucket of water at room temperature. You add a liter of hot water to it which makes the overall temperature of the bucket rise by a certain amount. Now, add another liter of cold water to it. The contrasting temperatures of water added to the bucket will cancel out each other, and the result will be a bucket of water at room temperature. The same rule applies while finding the additive inverse of a number. The additive inverse property holds good for both real numbers and complex numbers.

Additive Inverse of Real Numbers

The given number can be a whole number, a natural number, an integer, a fraction, a decimal, or any real number. The additive inverse of real numbers is just the negative of the given number.

Example	Given Number	Additive Inverse
Natural Numbers	12	-12
Whole Numbers	6	-6
Integers	-12	12
Fractions	-4/5	4/5
Decimals	2.5	-2.5

Additive Inverse of Complex Numbers

The algebraic property of complex numbers states the existence of additive inverse. Given any complex number z ∈ C, there is a unique complex number, denoted by -z, such that z + (-z) = 0. Moreover, if z = (x,y) with x,y ∈ R, then -z = (-x,-y).

Let Z = x + iy be the given complex number. Then its inverse is -Z = -x - iy. For example, the additive inverse of - i - 1 = - (- i - 1) = i + 1.

Additive Inverse of a Fraction

The additive inverse of a fraction a/b is -a/b, and vice-versa. It is because a/b + (-a/b) = 0. The additive inverse of a positive fraction is the same fraction with the negative sign, while for a negative fraction, its additive inverse is the same fraction without the negative sign.

Additive Inverse Formula

The general formula for the additive inverse of a number can be given in the form of the number itself. Any number when added to its negative will cancel out each other and give the overall sum as zero. We need to find the negative of the given number N. In other words, we need to find -1 × (N). Hence, we can say that:

Additive Inverse of N = -1 × (N)

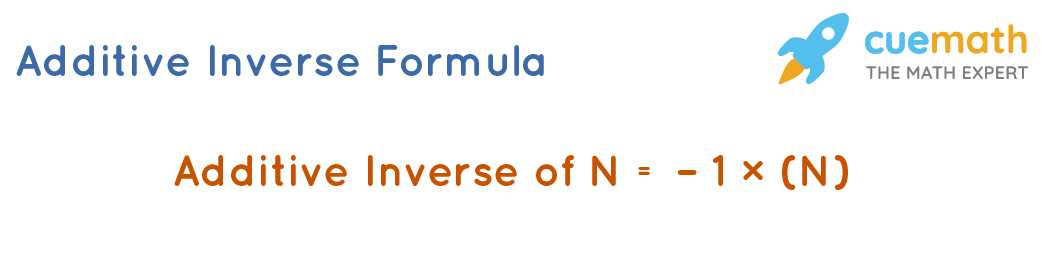
Additive Inverse and Multiplicative Inverse

There are two properties of numbers: multiplicative inverse and additive inverse property related to the multiplication and addition operation respectively. For a number x, - x is the additive inverse and 1/x is the multiplicative inverse. Let us understand the difference between additive inverse and multiplicative inverse with the help of the following table:

Additive Inverse	Multiplicative Inverse
To find the additive inverse, we change the sign of the number.	To find the multiplicative inverse, we take the reciprocal of the number.
It is added to the original number to get 0.	It is multiplied by the given number to get 1.
Equation: a + (-a) = 0	Equation: a × 1/a = 1

Additive Inverse in Algebraic Expressions

The property of additive inverse can be extended to algebraic expressions. Following the same rule as stated above, the additive inverse of an algebraic expression is one that makes the sum of all the terms zero. Note: The additive inverse of the expression is -(expression). The additive inverse of x2 + 1 is - (x2 + 1) = -x2 - 1.

For example, the additive inverse of 2x + 3y is -2x - 3y, making the sum of all the elements zero.

☛ Related Articles:

• Additive Inverse Calculator
• What is the additive inverse of -7?
• Additive Identity of Rational Numbers