Arc Length - Formula, How To Find Length Of An Arc, Examples

Arc Length

Arc length is better defined as the distance along the part of the circumference of any circle or any curve (arc). Any distance along the curved line that makes up the arc is known as the arc length. A part of a curve or a part of a circumference of a circle is called Arc. All of them have a curve in their shape. The length of an arc is longer than any straight line distance between its endpoints (a chord).

In particular, the length of an arc of a circle of radius 'r' that subtends an angle θ at the center is calculated by the formula rθ × (π/180) if the angle is in degrees and if the angle is in radians, then the arc length is rθ. Let 's see how to derive these formulas.

1.	What is Arc Length?
2.	Arc Length Formula
3.	How to Find Arc Length of a Curve?
4.	FAQs on Arc Length

What is Arc Length?

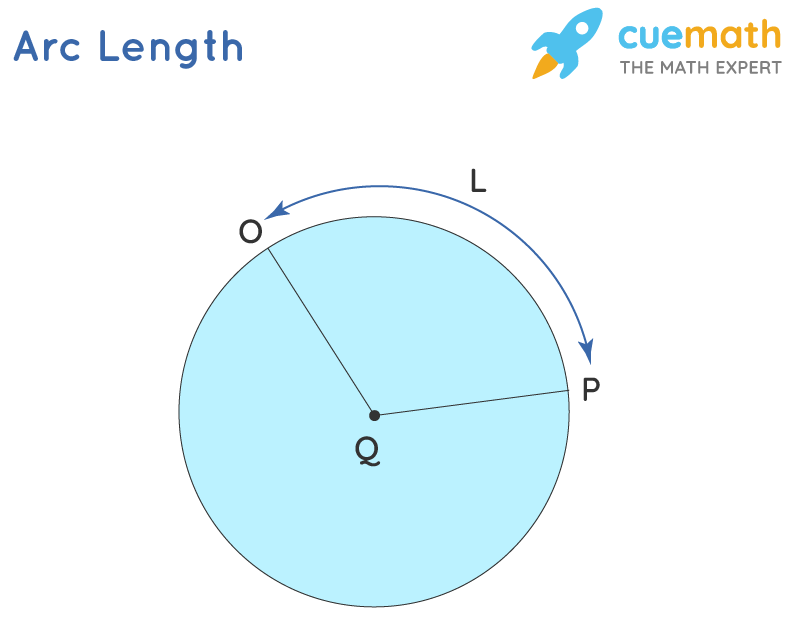
Thearc length is defined as the interspace between the two points along a section of a curve. An arc of a circle is any part of the circumference. The angle subtended by an arc at any point is the angle formed between the two line segments joining the center to the end-points of the arc. For example, in the circle shown below, OP is the arc of the circle with center Q. The arc length of this arc OP is given as L.

Arc Length Formula

To derive the arc length formula, let us recall what is the circumference of a full circle whose radius is 'r'. It is 2πr. But arc is just a part (in fact a fraction) of the total circumference. We know that the angle at the center in a full circle is 360°. If the angle subtended by an arc is θ°, then it means that the arc occupies a fraction of θ/360 out of the total circumference. Thus:

Arc length = θ/360 of 2πr = θ/360 × 2πr = rθ × π/180.

This is the arc length formula when the angle is in degrees. The length of an arc can be calculated using different formulas, based on the unit of the central angle of the arc. The measurements of the central angle can be given in degrees or radians, and accordingly, we calculate the arc length of a circle.

If θ is in radians, then the angle in degrees = θ × 180/π. By substituting this in the above formula,

Arc length = rθ × π/180 × 180/π = rθ.

Thus, the arc of a circle formula is θ times the radius of a circle, if the angle is in radians.

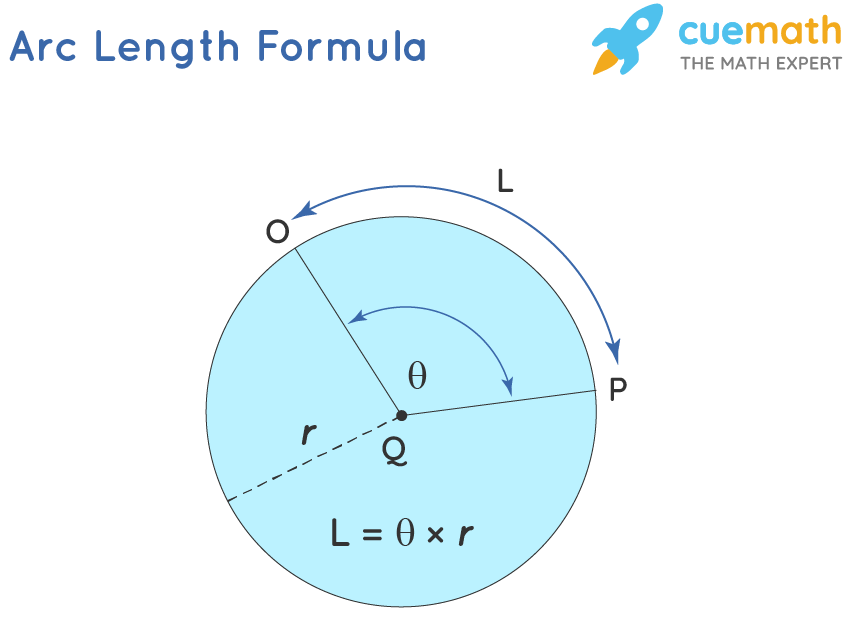
The arc length formula can be expressed as:

arc length, L = θ × r, when θ is in radian;

arc length, L = θ × (π/180) × r, where θ is in degrees,

where,

• L = Length of an Arc
• θ = Central angle of Arc
• r = Radius of the circle

Arc Length Formula in Radians

The arc length of a circle can be calculated using different formulas, based on the unit of the center angle of the arc. The arc length formula in radians can be expressed as,

Arc Length = θ × r

where,

• L = Arc Length
• θ = Center angle of the arc in radians
• r = Radius of the circle

How to Find Arc Length of a Curve?

The arc length of an arc of a circle can be calculated using different methods and formulas based on the given data. Some important cases are given below,

• find arc length with the radius and central angle
• find arc length without the radius
• find arc length without the central angle

How to Find Arc Length With the Radius and Central Angle?

The arc length of a circle can be calculated with the radius and central angle using the arc length formula,

• Length of an Arc = θ × r, where θ is in radian.
• Length of an Arc = θ × (π/180) × r, where θ is in degree.

How to Find Arc Length Without the Radius?

The arc length of a circle can be calculated without the radius using:

Central angle and the sector area:

• The sector area formula is, (θ/360º) × πr2, if θ is in degrees (or) (1/2) r2θ, if θ is in radians.
• Use this formula and solve for the radius 'r'. We need to use the square root in this process.
• Then find the arc length using the relevant formula.

Example: Calculate the arc length of a curve with sector area 25 square units and the central angle as 2 radians.

We have,

Sector area = 25 units

Central angle = 2 radians

• Step 1: Sector area = 25 ⇒ (1/2) r2(2) = 25
• Step 2: This gives r2 = 25. By taking square root on both sides, r = 5.
• Step 3: Arc length = rθ = 5 × 2 = 10 units

Thus, arc length = 10 units

Central angle and the chord length:

• The chord length formula is, 2r sin (θ/2).
• Use this formula and solve for the radius 'r'.
• Then its easy to find the arc length using the suitable formula.

Example: Calculate the arc length of a curve, whose endpoints touch a chord of the circle measuring 5 units. The central angle subtended by the arc is 2 radians.

We have,

Chord length = 5 units

Central angle = 2 radians

• Step 1: Chord length = 5 ⇒ 2r sin (2/2) = 5
• Step 2: 2r sin (1) = 5 ⇒ r = 5 / (2 × sin 1) = 2.97 units
• Step 3: Arc length = radius × central angle = 2.97 × 2 = 5.94 units

Thus, arc length = 5.94 units

How to Find Arc Length Without the Central Angle?

The arc length of a circle can be calculated without the angle using:

Radius and the sector area:

• Substitute the values of radius and sector area in the formula of sector area.
• Solve it for the central angle.
• Find the arc length.

Example: Calculate the arc length of a curve with a sector area 25 square units and radius as 2 units.

We have,

Sector area = 25 units

Central angle = 2 units

• Step 1: Sector area = 25 ⇒ (1/2) (2)2θ = 25.
• Step 2: Solving the above equation, we get θ = 12.5 radians.
• Step 3: Arc length = radius × central angle = 2 × 12.5 = 25 units

Thus, arc length = 25 units

Radius and chord length:

• Substitute the values of radius and chord length in the formula of chord length.
• Then solve for the central angle.
• Calculate the arc length.

Example: Calculate the arc length of a curve, whose endpoints touch a chord of the circle measuring 3 units. The radius of the circle is 2 units.

We have,

Chord length = 5 units

Central angle = 2 units

• Step 1: Chord length = 3 ⇒ 2(2) sin (θ/2) = 3
• Step 2: Solving this, we get: sin (θ/2) = 0.75 ⇒ θ/2 = sin-1(0.75) = 0.848 ⇒ θ = 1.696.
• Step 3: Arc length = radius × central angle = 2 × 1.696 = 3.392 units

Thus, arc length = 3.392 units

☛ Important Notes on Arc of a Circle:

Given below are key highlights on the concept of arc length.

• Arc Length = θ × r, where θ is in radians.
• Arc Length = θ × (π/180) × r, where θ is in degrees.

☛ Related Topics on Arc Length

Check out a few more interesting articles related to arc length to understand the topic more precisely.

• Arc Length Calculator
• Arc of a Circle Calculator