Area And Perimeter Of A Semicircle And Quadrant Of A Circle

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Area and Perimeter of a Semicircle and Quadrant of a Circle

We will learn how to find the Area and perimeter of a semicircle and Quadrant of a circle.

Area of a semicircle = \(\frac{1}{2}\)πr2

Perimeter of a semicircle = (π + 2)r.

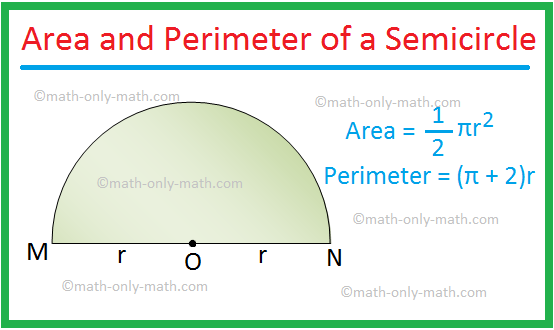
because a semicircle is a sector of sectorial angle 180°.

Area of a quadrant of a circle = \(\frac{1}{4}\)πr2.

Perimeter of a quadrant of a circle = (\(\frac{π}{2}\) + 2)r.

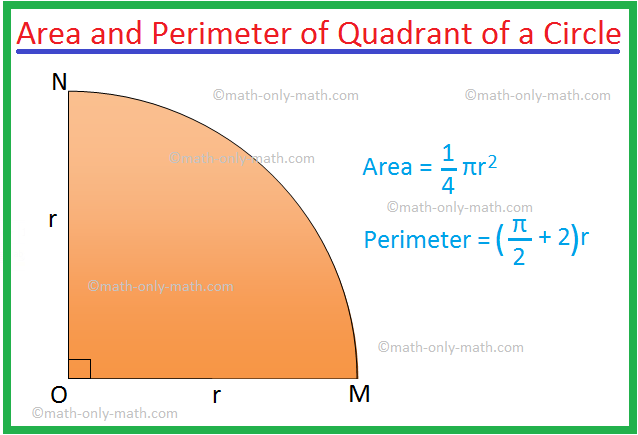
because a quadrant of a circle is a sector of the circle whose sectorial angle is 90°.

Here r is the radius of the circle.

Solved Examples on Area and perimeter of a semicircle and Quadrant of a circle:

1. The area of a semicircular region is 308 cm^2. Find its perimeter. (Use π = \(\frac{22}{7}\).)

Solution:

Let r be the radius. Then,

area = \(\frac{1}{2}\) ∙ πr^2

⟹ 308 cm^2 = \(\frac{1}{2}\) ∙ \(\frac{22}{7}\) ∙ r^2

⟹ 308 cm^2 = \(\frac{22}{14}\) ∙ r^2

⟹ \(\frac{22}{14}\) ∙ r^2 = 308 cm^2

⟹ r^2 = \(\frac{14}{22}\) ∙ 308 cm^2

⟹ r^2 = \(\frac{7}{11}\) ∙ 308 cm^2

⟹ r^2 = 7 × 28 cm^2

⟹ r^2 = 196 cm^2

⟹ r^2 = 14^2 cm^2

⟹ r = 14 cm.

Therefore, the radius of the circle is 14 cm.

Now, perimeter = (π + 2)r

                       = (\(\frac{22}{7}\) + 2) ∙ 14 cm

                       = \(\frac{36}{7}\)  ×  14 cm

                       = 36 × 2 cm

                       = 72 cm.

2. The perimeter of a sheet of paper in the shape of a quadrant of a circle is 75 cm. Find its area. (Use π = \(\frac{22}{7}\).)

Solution:

Let the radius be r. 

Then,

perimeter = (\(\frac{π}{2}\) + 2)r

⟹ 75 cm = (\(\frac{1}{2}\) ∙ π + 2)r

⟹ 75 cm = (\(\frac{ 1 }{2}\) ∙ \(\frac{22}{7}\)  + 2)r

⟹ 75 cm = (\(\frac{11}{7}\)  + 2)r

⟹ 75 cm = \(\frac{25}{7}\)r

⟹ \(\frac{25}{7}\)r = 75 cm

⟹ r = 75 × \(\frac{7}{25}\) cm

⟹ r = 3 × 7 cm

⟹ r = 21 cm.

Therefore, the radius of the circle is 21 cm.

Now, area = \(\frac{1}{4}\)πr^2

                = \(\frac{1}{4}\) ∙  \(\frac{22}{7}\) ∙ 21^2 cm^2

                = \(\frac{1}{4}\) ∙  \(\frac{22}{7}\) ∙ 21 ∙ 21 cm^2

                = \(\frac{693}{2}\) cm^2

                = 346.5 cm^2.

Therefore, area of the sheet of paper is 346.5 cm^2.

10th Grade Math

From Area and Perimeter of a Semicircle and Quadrant of a Circle to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math. Use this Google Search to find what you need.

New! Comments

Have your say about what you just read! Leave me a comment in the box below. Ask a Question or Answer a Question.

Share this page: What’s this?

FacebookXPinterestWhatsAppReddit ShareFacebookXPinterestWhatsAppReddit