Area Of Equilateral Triangle - GCSE Maths - Steps, Examples & More

Introduction What is an equilateral triangle? How to name a triangle How do we find the area of a triangle? Area of an equilateral triangle formula How to find the area of an equilateral triangle Area of equilateral triangle worksheet Area of equilateral triangles examples

↓

Example 1: given base length and height Example 2: given base length and height Example 3: finding the missing height using Pythagoras’ Theorem Example 4: using SOHCAHTOA to find the missing height Example 5: compound shapes Example 6: using the ½ab sin C formula Common misconceptions Practice area of equilateral triangle questions Area of equilateral triangle GCSE exam questions Learning checklist Next lessons Still Stuck?

GCSE Tutoring Programme

Our chosen students improved 1.19 of a grade on average - 0.45 more than those who didn't have the tutoring.

Teacher-trusted tutoring

In order to access this I need to be confident with:

Substitution Maths formulas Area of a quadrilateral Rearranging equations Pythagoras’ Theorem Trigonometry

This topic is relevant for:

Introduction What is an equilateral triangle? How to name a triangle How do we find the area of a triangle? Area of an equilateral triangle formula How to find the area of an equilateral triangle Area of equilateral triangle worksheet Area of equilateral triangles examples

↓

Example 1: given base length and height Example 2: given base length and height Example 3: finding the missing height using Pythagoras’ Theorem Example 4: using SOHCAHTOA to find the missing height Example 5: compound shapes Example 6: using the ½ab sin C formula Common misconceptions Practice area of equilateral triangle questions Area of equilateral triangle GCSE exam questions Learning checklist Next lessons Still Stuck? GCSE Maths Geometry and Measure Area

Area of an Equilateral Triangle

Area of an Equilateral Triangle

Here we will learn about the area of an equilateral triangle including how to find the area of an equilateral triangle with given lengths and how to calculate those lengths if they are not given.

There are also area of a triangle worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is an equilateral triangle?

An equilateral triangle is a triangle with all sides equal and all angles equal.

As the angles in a triangle add up to 180º this means that each of the angles in an equilateral triangle is 60º.

Since all sides are the same length it is a regular polygon.

What is an equilateral triangle?

How to name a triangle

We can identify a triangle by putting a capital letter on each vertex (corner).

We can then refer to each of the sides of the triangle by using two letters to describe where the line starts and ends.

We can refer to the entire triangle by using all three letters.

E.g.Name of sides:side AB, side AC, side BC

Name of triangle:triangle ABC

We use small lines on the sides to indicate that there are three equal sides in an equilateral triangle.

How do we find the area of a triangle?

In order to find the area of a triangle, we need to start with the area of a rectangle.

To find the area of a rectangle you must multiply adjacent sides together.

The area of the rectangle below would be calculated by multiplying the base × height (b × h):

We can split a rectangle into 2 congruent (identical) triangles.

So the area of each triangle is exactly half the area of the rectangle.

Area of an equilateral triangle formula

The formula to find the area of any triangle is:

\[\text { Area of a triangle }= \frac{\text { base } \times \text { height }}{2}\]

This can be shortened to:

\[A=\frac{1}{2} b h\]

where b is the base length and h is the height of the triangle.

Your final answer must be given in units2. (e.g. cm2, m2, mm2)

To find the area of an equilateral triangle when only the side length has been given, we will need to calculate the height of the triangle using Pythagoras’ Theorem or Trigonometry (SOHCAHTOA).

Finding the height using Pythagoras’ Theorem

Let the side length of the equilateral triangle represent the base, b.

Drawing a perpendicular line from the top vertex to the base forms the height, h, and also forms a right angled triangle with hypotenuse b and short sides h and \frac{1}{2}b.

\begin{aligned} h &=\sqrt{{{b}^{2}}-{{\left( \frac{1}{2}b \right)}^{2}}} \\\\ & =\sqrt{\frac{3}{4}{{b}^{2}}} \\\\ & =\frac{\sqrt{3}}{2}b \end{aligned}

Finding the height using SOHCAHTOA

Let the side length of the equilateral triangle represent the base, b.

Drawing a perpendicular line from the top vertex to the base forms the height, h, and also forms a right angled triangle with hypotenuse b and angle 60^{\circ}.

\sin \left( 60 \right)=\frac{h}{b}

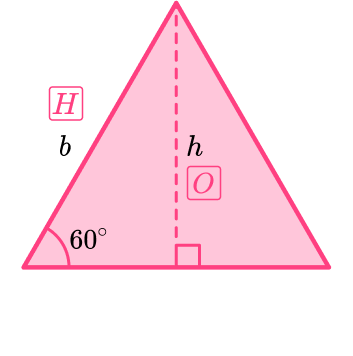
So, h=b\sin \left( 60 \right)

We can also find the area of the equilateral triangle using the area of a triangle formula

\text{Area }=\frac{1}{2}ab\sin C

The formula would give the area as

\text{Area }=\frac{1}{2}{{b}^{2}}\sin \left( 60 \right)

Using the exact value of \sin \left( 60 \right)=\frac{\sqrt{3}}{2}, this gives us

Area of an equilateral triangle =\frac{\sqrt{3}}{4}{{b}^{2}}

What is the formula to calculate the area of an equilateral triangle?

How to find the area of an equilateral triangle

In order to find the area of an equilateral triangle:

1. Identify the height and base length of your triangle if given. (You might need to calculate one of these values).
2. Write the appropriate area formula A=\frac{1}{2} b h or A=\frac{1}{2}{{b}^{2}}\sin \left( 60 \right)
3. Substitute the values into the formula
4. Calculate

Explain how to find the area of an equilateral triangle in 4 steps.

Area of equilateral triangle worksheet

Get your free area of an equilateral triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE x

Area of equilateral triangle worksheet

Get your free area of an equilateral triangle worksheet of 20+ questions and answers. Includes reasoning and applied questions.

DOWNLOAD FREE

Related lessons on area

Area of an equilateral triangle is part of our series of lessons to support revision on area. You may find it helpful to start with the main area lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• Area
• Area of a circle
• Area of a quadrilateral
• Area of a trapezium
• Area of a parallelogram
• Area of compound shapes
• Pi r squared
• Area of a rhombus
• Area of a right angled triangle
• Area of an isosceles triangle
• Area of a triangle
• How to work out area
• Area of a rectangle
• Area of a hexagon
• Area of a pentagon

Area of equilateral triangles examples

Example 1: given base length and height

Find the area of the triangle below:

1. Identify the height and base length of the triangle if given.

h = 2.6cm

b = 3cm

2Write down the appropriate formula.

\[A=\frac{1}{2} b h\]

3Substitute the values into the formula.

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(3)(2.6) \end{aligned}\]

4Calculate.

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(3)(2.6)\\\\ &=3.9cm^2 \end{aligned}\]

Remember: Your final answer must be in units squared.

Example 2: given base length and height

Find the area of the triangle below:

Identify the height and base length of the triangle if given.

h = 430cm

b = 5m

Note: You have 2 different units here. You must convert them to a common unit:

430cm = 4.3m

\[\begin{array}{l} h = 4.3m\\\\ b = 5m \end{array}\]

Write down the appropriate formula.

\[A=\frac{1}{2} b h\]

Substitute the values into the formula.

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(5)(4.3) \end{aligned} \]

Calculate.

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(5)(4.3)\\\\ &=10.75m^2 \end{aligned} \]

Remember: Your final answer must be in units squared.

Example 3: finding the missing height using Pythagoras’ Theorem

Find the area of triangle ABC below:

Identify the height and base length of the triangle if given.

b = 8mm

In this question, we are given one side length of the triangle. We are missing the height of the equilateral triangle. 

To calculate the height of an equilateral triangle using the Pythagorean Theorem but we must split the equilateral triangle into two equal right triangles with one of the sides of the equilateral triangle as the hypotenuse. 

Draw a straight line from the top vertex to the midpoint of the base. This will create two congruent right triangles with a hypotenuse of 8mm.

Using one of the right angled triangles we can apply Pythagorean Theorem:

\begin{array}{l} h^{2}&=8^{2}-4^{2} \\\\ h^{2}&=64-16 \\\\ h^{2}&=48 \\\\ h&=\sqrt{48} \\\\ h &= 6.92820… \mathrm{~mm} \end{array}

Write down the appropriate formula.

\[A=\frac{1}{2} b h\]

Substitute the values into the formula.

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(8)(6.928…) \end{aligned}\]

Calculate.

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(8)(6.928…)\\\\ &=27.7mm^2 (1.d.p) \end{aligned} \]

Remember: Your final answer must be in units squared.

Example 4: using SOHCAHTOA to find the missing height

Below is an equilateral triangle with side length 9 \, cm.

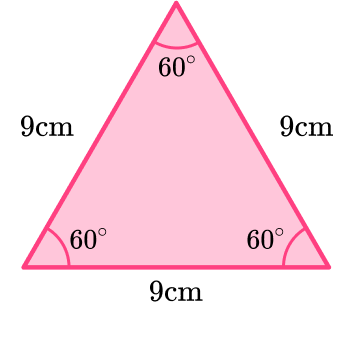
Find the area of the triangle.

Identify the height and base length of your triangle if given. (You might need to calculate one of these values)

The base of the triangle is 9 \, cm. We can calculate the height using SOHCAHTOA

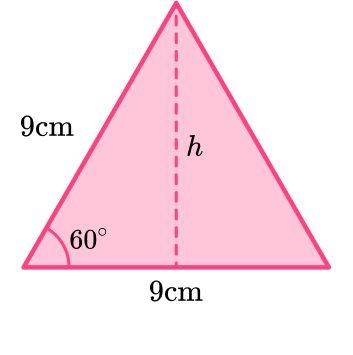
\begin{aligned} & h=9\sin \left( 60 \right) \\\\ & =7.794... \, cm \end{aligned}

Write down the appropriate formula.

\[A=\frac{1}{2} b h\]

Substitute the values into the formula.

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(9)(7.79) \end{aligned} \]

Calculate.

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(9)(7.79)\\\\ &=35.07 \, cm^2 \end{aligned} \]

Example 5: compound shapes

Below is the layout for a new garden plot that needs to be filled with soil. Each bag of soil costs £4.50 and covers an area of 2.5m2. How much would it cost to cover the entire plot with soil?

Identify the height and base length of the triangle if given.

Split the plan into 2 shapes. You have a rectangle and a right angled triangle.

For the triangle:

b = 7.5m

h = 6.5m

Write down the appropriate formula.

\[A=\frac{1}{2} b h\]

Substitute the values into the formula.

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(7.5)(6.5) \end{aligned} \]

Calculate.

\[\begin{aligned} A &=\frac{1}{2} b h \\\\ &=\frac{1}{2}(7.5)(6.5)\\\\ &=24.4m^2 (1.d.p) \end{aligned} \]

Now you must find the area of the rectangle:

\[\begin{aligned} \text { Area of a rectangle }&=l \times w \\\\ &=5 \times 7.5 \\\\ &=37.5 m^{2} \\\\ \end{aligned} \]

Total Area = 24.4 + 37.5 = 61.9m2

Now divide 61.9 by 2.5 since one bag of soil only covers an area of 2.5m2:

61.9 ÷ 2.5 = 24.76  which means you have to buy 25 bags of soil (you cannot buy half a bag of soil).

Now to work out the cost: 25 bags of soil × £4.50 = £112.50

The total cost to fill the plot with soil is £112.50.

Example 6: using the ½ab sin C formula

Below is an equilateral triangle with side length 15 \, cm.

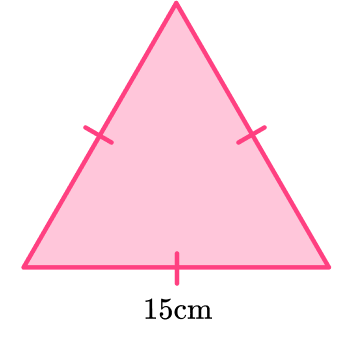
Find the area of the triangle.

Identify the height and base length of your triangle if given. (You might need to calculate one of these values)

We know all sides are of length 15 \, cm and each angle is 60^{\circ}, so we can use the A=\frac{1}{2}{{b}^{2}}\sin \left( 60 \right) formula.

Write down the appropriate formula.

\[A=\frac{1}{2}{{b}^{2}}\sin \left( 60 \right)\]

Substitute the values into the formula.

\[A=\frac{1}{2}{{15}^{2}}\sin \left( 60 \right) \]

Calculate.

\[\begin{aligned} A& =\frac{1}{2}{{\left( 15 \right)}^{2}}\sin \left( 60 \right) \\\\ & =97.43 \, cm^{2} \end{aligned} \]

Common misconceptions

• The height of an equilateral triangle is not the same as the side length

When dealing with an equilateral triangle’s area it is important to note that even though the length of all sides are equal, the height is not the same as well. It will either be given in the question or you will have to calculate it.

• Units

It is common to forget the units for area in the final answer. When calculating area, your answer must always have units squared.

Practice area of equilateral triangle questions

1. Find the area of the triangle below:

55.2 cm^2 27.6 cm^2 13.8 cm^2 110.4 cm^2

The area of the triangle is given by

\frac{1}{2} \times 8 \times 6.9 = 27.6cm^{2}

2. Find the area of the triangle below:

87m^2 43.5m^2 4350m^2 4.35m^2

We convert the height into metres and then use the formula,

\frac{1}{2} \times 10 \times 8.7 =  43.5m^{2}

3. Shown below is a rhino enclosure. Each rhino needs a minimum of 9m^2 to roam around. What is the maximum number of rhinos that can fit into this enclosure?

9 rhinos 10 rhinos 5 rhinos 18 rhinos

The shape can be split into a rectangle and triangle.

The area of the rectangle is:

8.5 \times 6 = 51m^{2}

The area of the triangle is:

\frac{1}{2} \times 8.5 \times 7.4 = 31.45m^{2}

This means the total area is:

51 + 31.45=82.45m^{2}

By considering multiples of 9 , we conclude that 9 rhinos will fit.

4. Find the area of the triangle below:

72cm^2 36cm^2 62.4cm^2 31.2cm^2

The height can be calculated using Pythagoras’ Theorem:

Height = \sqrt{12^{2}-6^{2}} Height = 10.392…

Then using the formula with measures for the base and height:

\frac{1}{2} \times 12 \times 10.392 = 62.4 (1.d.p)

Area of equilateral triangle GCSE exam questions

1. This regular hexagon is made using six equilateral triangles. 

Find the area of the hexagon.

(4 marks)

Show answer 20.8 \div 2 = 10.4

(1)

One triangle:

A= \frac{1}{2} \times 12 \times 10.4

(1)

A = 62.4cm^{2}

(1)

Total area:

6 \times 62.4=374.4cm^{2}

(1)

2. Lily wants to hire a plasterer to plaster the following wall.

Brian charges \pounds 20 + \pounds 2 per square metre.

Natalie charges a flat rate of \pounds 150 .

Which plasterer would be the cheapest?

(5 marks)

Show answer

Area of rectangle:

\begin{aligned}A&=6 \times 8\\\\A&=48m^{2}\end{aligned}

(1)

 Area of triangle:

\begin{aligned} A&=\frac{1}{2} \times 6 \times 5.2\\\\ A&=15.6m^{2} \end{aligned}

(1)

 Total area:

48+15.6=63.6m^{2}

(1)

Brian:

\pounds 20 + 63.6 \times \pounds 2 = \pounds 147.20

(1)

Brian would be cheaper

(1)

3. Find the area of an equilateral triangle with sides of length 10cm .

(4 marks)

Show answer

Find height using Pythagoras Theorem:

h^{2}=10^{2}-5^{2}

(1)

h^{2}=75 h=8.6602...cm

(1)

A=\frac{1}{2} \times 10 \times 8.7...

(1)

A=43.5cm^{2}

(1)

Learning checklist:

You have now learned how to:

• Apply a formula to calculate and solve problems involving the area of triangles
• Use Pythagoras’ Theorem to solve problems involving triangles

The next lessons are

• How to work out perimeter
• Symmetry
• Circles, sectors and arcs

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Introduction What is an equilateral triangle? How to name a triangle How do we find the area of a triangle? Area of an equilateral triangle formula How to find the area of an equilateral triangle Area of equilateral triangle worksheet Area of equilateral triangles examples

↓

Example 1: given base length and height Example 2: given base length and height Example 3: finding the missing height using Pythagoras’ Theorem Example 4: using SOHCAHTOA to find the missing height Example 5: compound shapes Example 6: using the ½ab sin C formula Common misconceptions Practice area of equilateral triangle questions Area of equilateral triangle GCSE exam questions Learning checklist Next lessons Still Stuck? We use essential and non-essential cookies to improve the experience on our website. Please read our Cookies Policy for information on how we use cookies and how to manage or change your cookie settings.AcceptPrivacy & Cookies Policy Close

Privacy Overview

This website uses cookies to improve your experience while you navigate through the website. Out of these, the cookies that are categorized as necessary are stored on your browser as they are essential for the working of basic functionalities of the website. We also use third-party cookies that help us analyze and understand how you use this website. These cookies will be stored in your browser only with your consent. You also have the option to opt-out of these cookies. But opting out of some of these cookies may affect your browsing experience. Necessary Necessary Always Enabled Necessary cookies are absolutely essential for the website to function properly. This category only includes cookies that ensures basic functionalities and security features of the website. These cookies do not store any personal information. Non-necessary Non-necessary Any cookies that may not be particularly necessary for the website to function and is used specifically to collect user personal data via analytics, ads, other embedded contents are termed as non-necessary cookies. It is mandatory to procure user consent prior to running these cookies on your website. SAVE & ACCEPT