Area Of Scalene Triangle - Formula, Examples, Definition - Cuemath

Area of Scalene Triangle

The total area of a scalene triangle is the area between the boundaries of the scalene triangle. A scalene triangle is a special type of triangle where all three sides of the triangle are of different lengths as well as the angles are of different measures. Although all the angles of a scalene triangle are different the sum of all the interior angles of the triangle is still 180 degrees. We will discuss the area of the scalene triangle, the formula for calculating the area along with the solved examples, and a few practice questions in the end.

1.	What is the Area of a Scalene Triangle?
2.	Area of a Scalene Triangle Formula
3.	Calculation of Area
4.	List of Area of Scalene Triangle Formula
5.	FAQs on Area of Scalene Triangle

What is the Area of Scalene Triangle?

The area of a scalene triangle can be defined as the amount of space covered by a flat surface inside the scalene triangle. It is measured as the "number of" square units (square centimeters, square inches, square feet, etc.).

Area of a Scalene Triangle Formula

The formula of the area of the scalene triangle is used to find the area occupied by the scalene triangle within its boundary. The area of the scalene triangle is obtained by taking half of the product of the base to the height of the triangle. Thus, the formula for the area of the scalene triangle, with a base "b" and height "h" is"(1/2) bh".

Or, Area of a Scalene Triangle = [(1/2) × base × height] square units

Calculation of Area of a Scalene Triangle

As the triangle has 6 quantities namely 3 sides and 3 angles, the area of a triangle is calculated via various formulas depending upon the known quantities of the triangle.

• Area of Scalene Triangle With Base and Height

When the base and height of the scalene triangle is known, then the area of a triangle is:

Area of a triangle = (1/2) × Base × Height

where b and h are the base and height of the triangle respectively.

• Area of Scalene Triangle Using Heron's Formula

Heron's formula is applicable when all three sides of the triangle are known to us.

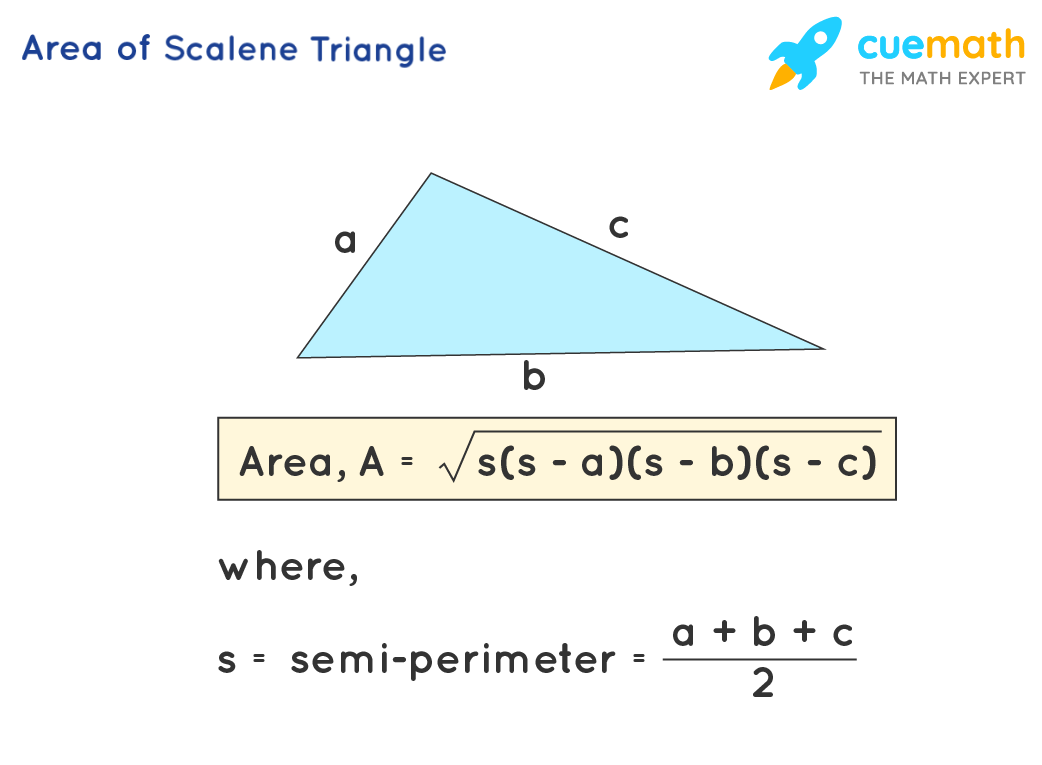
Consider the triangle ABC with sides a, b, and c has shown in the image.

Heron’s formula is: \(\text{Area} = \sqrt{s(s-a)(s-b)(s-c)}\)

where, a, b, c are the side length of the triangle, and, s is the semi-perimeter and equals (a+b+c)/2.

• Area of the Scalene Triangle With 2 Sides and Included Angle (SAS)

We can find the scalene triangle's area when the length of its two sides and the included angle are given.

1. When two sides b and c and included angle A is known, the area of the triangle is, Area = (1/2) bc × sin A

2. When sides a and c and included angle B is known, the area of the triangle is, Area = (1/2) ac × sin B

3. When sides a and b and included angle C is known, the area of the triangle is, Area = (1/2) ab × sin C

List of Area of Scalene Triangle Formula List

The area of a triangle can be calculated using the formulas discussed above. Here is a list of all those formulas:

Area of the ScaleneTriangle When	Formula
Base and height of a triangle are given	(1/2) × base × height
Sides of a triangle are given	\(\sqrt {s(s - a)(s - b)(s - c)} \) where a, b, c are the sides and s is the semi-perimeter, s = (a + b + c)/2
Two sides and the included angle are given	\(\dfrac{1}{2}\: {\text{side}_1} \times {\text{side}_2} \times \sinθ\) where 'θ' is the angle between the given two sides.

Related Topics

Listed below are a few topics related to area of scalene triangle, take a look.

• Scalene Triangle Formula
• Right Scalene Triangle
• Acute Scalene Triangle
• Classifying Triangles