Area Of Triangle In Coordinate Geometry - Formula - Cuemath

Area of Triangle in Coordinate Geometry

In Geometry, a triangle is a three-sided polygon that has three edges and three vertices. The area of triangle in coordinate geometry is calculated by the formula (1/2) |x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)|, where (x1, y1), (x2, y2), and (x3, y3) are the vertices of the triangle triangle.

The area of the triangle is the space covered by the triangle in a two-dimensional plane. The formula for the area of a triangle is (1/2) × base × altitude. We will use this formula to find out the area of a triangle in coordinate geometry.

1.	What is the Area of a Triangle in Coordinate Geometry?
2.	Proof of Area of Triangle Formula in Coordinate Geometry
3.	Area of a Triangle Using Determinants
4.	FAQs on Area of a Triangle in Coordinate Geometry

What is the Area of a Triangle in Coordinate Geometry?

Coordinate geometry is defined as the study of geometry using coordinate points. The area of a triangle in coordinate geometry can be calculated if the three vertices of the triangle are given in the coordinate plane. The area of a triangle in coordinate geometry is defined as the area or space covered by it in the 2-D coordinate plane. Let us understand the concept of the area of a triangle in coordinate geometry better using the example given below,

Consider these three points: A(−2,1), B(3,2), C(1,5). If you plot these three points in the plane, you will find that they are non-collinear, which means that they can be the vertices of a triangle, as shown below:

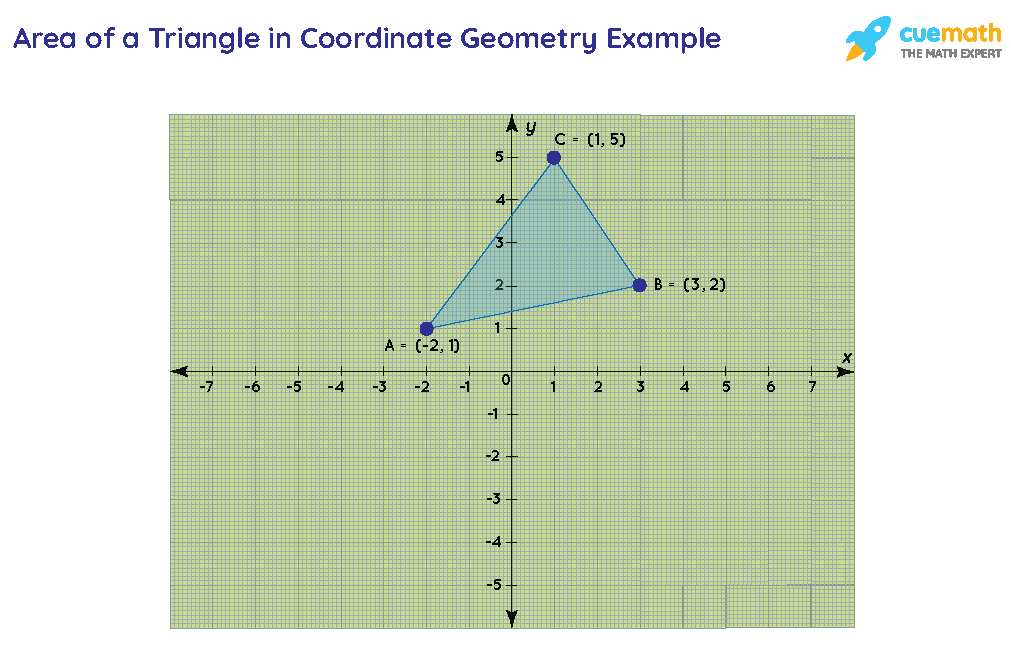
The area covered by the triangle ABC in the x-y plane is the region marked in blue. Now, with the help of coordinate geometry, we can find the area of this triangle.

Area of a Triangle Formula in Coordinate Geometry

If (x1, y1), (x2, y2), and (x3, y3) are the three vertices of a triangle on the coordinate plane, then its area is calculated by the formula (1/2) |x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)|. Let us learn more about it in the following section.

Proof of Area of Triangle Formula in Coordinate Geometry

In coordinate geometry, if we need to find the area of a triangle, we use the coordinates of the three vertices. Consider ΔABC as given in the figure below with vertices A(x1, y1), B(x2, y2), and C(x3, y3). In this figure, we have drawn perpendiculars AE, CF, and BD from the vertices of the triangle to the horizontal axis. Notice that three trapeziums are formed: BAED, ACFE, and BCFD.

We can express the area of a triangle in terms of the areas of these three trapeziums.

Area(ΔABC) = Area(Trap.BAED) + Area(Trap.ACFE) - Area(Trap.BCFD)

Now, the area of a trapezium in terms of the lengths of the parallel sides (the bases of the trapezium) and the distance between the parallel sides (the height of the trapezium):

Trapezium Area = (1/2) × Sum of bases × Height

Consider any one trapezium, say BAED. Its bases are BD and AE, and its height is DE. BD and AE can easily be seen to be the y coordinates of B and A, while DE is the difference between the x coordinates of A and B. Similarly, the bases and heights of the other two trapeziums can be easily calculated. Thus, we have:

Area(Trap.BAED) = (1/2) × (BD + AE) × DE

= (1/2) × (y2 + y1) × (x1 − x2)

Area(Trap.ACFE) = (1/2) × (AE + CF) × EF

= (1/2) × (y1 + y3) × (x3 − x1)

Area(Trap.BCFD) = (1/2) × (BD + CF) × DF

= (1/2) × (y2 + y3) × (x3 − x2)

The expression for the area of the triangle in terms of the coordinates of its vertices can thus be given as,

Area(ΔABC) = Area(Trap.BAED) + Area(Trap.ACFE) - Area(Trap.BCFD)

= (1/2) × [(y2 + y1) × (x1 − x2)] + (1/2) × [(y1 + y3) × (x3 − x1)] - (1/2) × [(y2 + y3) × (x3 − x2)]

However, we should try to simplify it so that it is easy to remember.

For that, we simplify the product of the two brackets in each terms:

= (1/2) (x1y2 − x2y2 + x1y1 − x2y1) + (1/2) (x3 y1 − x1y1 + x3y3 − x1y3) − (1/2)(x3y2 − x2y2 + x3y3 − x2y3)

Take the common term 1/2 outside the bracket.

=(1/2) (x1y2 − x2y2 + x1y1 − x2y1 − x3 y1 − x1y1 + x3y3 − x1y3 − x3y2 + x2y2 - x3y3 + x2y3)

Thus,

Area(ΔABC) = (1/2){x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)}

As the area is always positive. Hence, we take the absolute value sign.

(ΔABC) = (1/2) |x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)|

This is a symmetric expression, and there is an easy technique to remember it, which we will now discuss as Determinants Method.

Area of a Triangle Using Determinant Method

To calculate the area of a triangle using determinants, we use the formula as shown below,

Area = 1/2 \(\begin{bmatrix}{{x_1}}&{{y_1}}&{{1}}\\{{x_2}}&{{y_2}}&{{1}}\\{x_3}&{y_3}&1\end{bmatrix}\)

Let us solve the above expression to obtain the formula for the area of a triangle using coordinates. We will solve the determinant along the first column.

Now, the first term in the expression for the area is \({x_1}\left( {{y_2} - {y_3}} \right)\). To obtain this, we solve determinants for the first term in the first column. Ignore the terms in the first row and column other than the first term and proceed according to the following visual representation (the cross arrows represent multiplication). Solving determinant we get, x1(y2 - y3).

The second term in the expression for the area is x2(y3 − y1). To obtain this, we solve determinant for the second term in the first column. Ignore the terms in the second row and first column other than the first term in the second column. Solving determinant, we get -x2(y1 - y3) = x2(\({y_3} - {y_1}\)):

Next, the third term in the expression for the area is \({x_3}\left( {{y_1} - {y_2}} \right)\). To obtain this, we solve determinant for the third term in the first column. Ignore the terms in the first row and third column other than the first term in the third column:

Finally, we add these three terms to get the area (and divided by a factor of 2, because we had this factor in the original expression we determined):

Area = (1/2) |x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2)|

Note that we have put a modulus sign (vertical bars) around our algebraic expression, and removed the negative sign because the area is always positive, which we obtained in the original expression. So even if we get a negative value through the algebraic expression, the modulus sign will ensure that it gets converted to a positive value.

We can write the above expression for area compactly in determinant form as follows:

\(A = \frac{1}{2}\;\left| {\begin{array}{*{20}{c}}{{x_1}}&{{y_1}}&{{1}}\\{{x_2}}&{{y_2}}&{{1}}\\{x_3}&{y_3}&1\end{array}} \right|\)

To know more about this method, click here.

Important Notes on Area of Triangle in Coordinate Geometry:

• The area of a triangle cannot be negative. In case we get the answer in negative terms, we should consider the numerical value of the area (i.e., ignore the negative sign).
• To find the area of a triangle in coordinate geometry can also be found by finding the length of three sides of a triangle using the distance formula and then applying Heron's formula. To know more information about this, click here.
• If three points A(x1,y1), B(x2,y2), and C(x3,y3) are collinear, then x1(y2 − y3) + x2(y3 − y1) + x3(y1 − y2) = 0.

☛ Related Topics:

• Area of triangle calculator
• Area of Equilateral Triangle
• Area of Isosceles Triangle
• Area of Scalene Triangle