Area Of Triangle With 3 Sides - Formula, Definition, Examples

Area of Triangle with 3 Sides

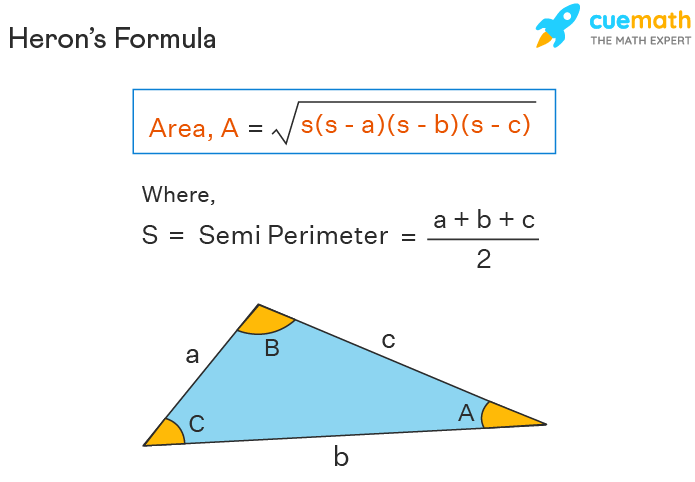
In order to find the area of triangle with 3 sides, we use the Heron's Formula. Using this, the area of a triangle (A) with 3 sides a, b, and c is calculated using the formula A = √[s(s-a)(s-b)(s-c)], where 's' is the semi-perimeter of the triangle given by s = (a + b + c)/2.

The area of a triangle can be calculated with the help of various formulas. The basic formula that is used to find the area of a triangle is ½ × Base × Height where "Base" is the side of the triangle on which the altitude is formed, and "Height" is the length of the altitude drawn to the "Base" from its opposite vertex. However, if the altitude of a triangle is not known, and we need to find the area of triangle with 3 different sides, the Heron's formula is used. This formula was derived by a Greek mathematician known as the Heron of Alexandria.

1.	Area of Triangle with 3 Sides Formula
2.	Proof of Area of Triangle with 3 Sides Formula
3.	How to Find Area of Triangle with Three Sides?
4.	Area of Triangle With 3 Equal Sides
5.	FAQs on Area of Triangle with 3 Sides

Area of Triangle with 3 Sides Formula

In order to find the area of a triangle with 3 sides, we use the Heron's formula which says if a, b, and c are the three sides of a triangle, then its area is,

Area = √[s(s-a)(s-b)(s-c)]

Here, "s" is the semi-perimeter of the triangle, i.e., s = (a + b + c)/2.

Let us see how to find the area of a triangle with 3 sides given as: 3, 6, and 7. We know that a = 3, b = 6, and c = 7, the semi-perimeter is, s = (a + b + c)/2 = (3 + 6 + 7)/2 = 8. We will find the area of the triangle using the Heron's formula.

A = √[s(s-a)(s-b)(s-c)]

= √[8(8-3)(8-6)(8-7)]

= √[8 × 5 × 2 × 1]

= √(80)

≈ 8.94

☛ Also Check: Triangle Area Calculator With 3 sides

Proof of Area of Triangle with 3 Sides Formula

The proof of the formula for the area of triangle with 3 sides can be derived in the following way.

Consider the triangle shown above with sides a, b, c, and the opposite angles to the sides as angle A, angle B, angle C.

Using law of cosines, cos A = (b2 + c2 - a2) / 2bc.

Using one of the Trigonometric identities,

sin2 A = 1 - cos2 A

\( \begin{align}\sin A &= \sqrt{1-\cos^2A}\\[0.2cm]\sin A &= \sqrt{1 - \dfrac{(b^2+c^2-a^2)^2}{4b^2c^2}} \\[0.2cm] \sin A &= \dfrac{\sqrt{4b^2c^2 - (b^2+c^2-a^2)^2}}{2bc} \\[0.2cm] \dfrac{1}{2} bc \sin A& = \dfrac{\sqrt{4b^2c^2 - (b^2+c^2-a^2)^2}}{4} \end{align}\)

We know that one of the formulas of the area of a triangle is ½ bc sin A. Thus, the area of triangle = \(\dfrac{\sqrt{4b^2c^2 - (b^2+c^2-a^2)}}{4}\).

Now, we will derive Heron's formula using the above formula just by applying some algebraic techniques. The above formula can be written as:

\( \begin{align} &\text{Area }\\[0.2cm] &= \dfrac{\sqrt{(2bc)^2- (b^2+c^2-a^2)^2}}{4}\\[0.2cm] &= \dfrac{1}{4} \sqrt{[ (b^2+c^2+2bc) - a^2] [ a^2 - (b^2+c^2-2bc)]}\\[0.2cm] &= \dfrac{1}{4} \sqrt{[ (b+c)^2-a^2] [a^2-(b-c)^2]}\\[0.2cm] &= \dfrac{1}{4} \sqrt{(b+c+a)(b+c-a)(a+b-c)(a-b+c)}\\[0.2cm] \end{align} \)

We know that the perimeter of triangle = (a + b + c) and hence semi-perimeter is, s = (a + b + c)/2. From this,

a + b + c = 2s

b + c - a = 2s - 2a

a + b - c = 2s - 2c

a - b + c = 2s - 2b

Substituting all these values in the last step,

\( \begin{align}& \text{Area } \\[0.2cm]&= \dfrac{1}{4} \sqrt{2s (2s-2a)(2s-2c)(2s-2b)}\\[0.2cm] &= \dfrac{4}{4} \sqrt{s(s-a)(s-c)(s-b)}\\[0.2cm] &= \sqrt{s(s-a)(s-b)(s-c)} \end{align}\)

Hence, we proved the Heron's formula.

How to Find Area of Triangle with Three Sides?

Consider a triangle with 3 sides given as a, b, and c. Follow the steps below to find its area:

• Step 1: Find semi-perimeter (s) by using the formula s = (a+b+c)/2.
• Step 2: Compute the differences (s - a), (s - b), and (s - c).
• Step 3: Compute the square root of [s(s - a)(s - b)(s - c)].

Example: Calculate the area of triangle with three sides 3, 4, and 5.

Solution: Let a = 3, b = 4, and c = 5.

• Step 1: s = (a + b + c)/2 = (3 + 4 + 5)/2 = 6.
• Step 2: (s - a) = 6 - 3 = 3; (s - b) = 6 - 4 = 2; (s - c) = 6 - 5 = 1.
• Step 3: Area = √[s(s-a)(s-b)(s-c)] = √(6 × 3 × 2 × 1) = 6.

Note: To simplify square roots with big products such as √(21 × 3 × 11 × 7) easily, do prime factorization of each number, then group pairs of numbers.

Area of Triangle With 3 Equal Sides

A triangle with 3 equal sides is known as an equilateral triangle. We know that the area of an equilateral triangle with side 'a' is √3/4 × a2. We can derive this formula by using the above formula of triangle area with three sides. Here, a = b = c = a. Using this, perimeter is 3a and semi-perimeter is s = 3a/2 and (s - a) = (3a/2) - a = a/2. Then the area by Heron's formula is:

A = √[s(s - a)(s - b)(s - c)]

= √ s (s - a) (s - a) (s - a)

= √(3a/2) (a/2) (a/2) (a/2)

= √3a2/4

Hence, the formula for triangle area with 3 equal sides is derived.

☛ Also Check: Area of triangle with 3 Equal sides Calculator