Changing Summation Limits | The Infinite Series Module - UBC Blogs

The Infinite Series Module A Set of Open Resources on Infinite Series Skip to content

• Home
• About the ISM
  • For Instructors
  • Technical Requirements
  • Copyright
  • Development of the ISM
• Units
  • Unit 1: Sequences and Series
    • Infinite Sequences
      • Introduction to Infinite Sequences
      • Convergence of Infinite Sequences
      • Convergence of Infinite Sequences Example
      • Relationship to Limits of Functions
      • Limit Laws for Infinite Sequences
      • Limit Laws Example
      • Relationship to Sequences of Absolute Values
      • Example Relating Sequences of Absolute Values
      • Squeeze Theorem for Sequences
      • Squeeze Theorem Example
      • Example: {rn}
      • Videos on Infinite Sequences
      • Final Thoughts on Infinite Sequences
    • Sigma Notation
      • Introduction to Sigma Notation
      • Sigma Notation Terminology
      • Sigma Notation Properties
      • Changing Summation Limits
      • Example: Changing the Summation Limits
      • Videos on Sigma Notation
      • Final Thoughts on Sigma Notation
    • Infinite Series
      • Introduction to Infinite Series
      • Convergence of Infinite Series
      • The Geometric Series
      • Geometric Series Example
      • Converting an Infinite Decimal Expansion to a Rational Number
      • Finding the Sum of an Infinite Series
      • A Geometric Series Problem with Shifting Indicies
      • Koch Snowflake Example
      • Videos on the Introduction to Infinite Series
      • Final Thoughts on Infinite Series
    • Properties of Convergent Series
      • The Properties of Convergent Series
      • Example: Properties of Convergent Series
    • The Telescoping and Harmonic Series
      • Introduction: Telescoping and Harmonic Series
      • The Harmonic Series
      • The Telescoping Series
      • Videos on Telescoping and Harmonic Series
      • Final Notes on Harmonic and Telescoping Series
  • Unit 2: Convergence Tests
    • The Divergence Test
      • Introduction to the Divergence Test
      • A Useful Theorem
      • The Divergence Test
      • A Divergence Test Flowchart
      • Simple Divergence Test Example
      • Divergence Test With Square Roots
      • Divergence Test with arctan
      • Video Examples for the Divergence Test
      • Final Thoughts on the Divergence Test
    • The Integral Test
      • A Motivating Problem for The Integral Test
      • A Second Motivating Problem for The Integral Test
      • Theorem: The Integral Test
      • An Integral Test Flowchart
      • Integral Test Example
      • Example: Integral Test with a Logarithm
      • The p-series
      • Videos on the Integral Test
      • Final Thoughts on The Integral Test
    • The Alternating Series Test
      • A Motivating Problem for the Alternating Series Test
      • The Alternating Series Test
      • An Alternating Series Test Concept Map
      • Return to Our Motivating Example
      • Alternating Series Test Videos
    • The Ratio Test
      • Introduction to the Ratio Test
      • The Ratio Test
      • The Ratio Test Flowchart
      • A Simple Ratio Test Example
      • Ratio Test Example with an Exponent
      • Videos on The Ratio Test
      • Final Thoughts on the Ratio Test
    • Review of Convergence Tests
      • Strategies for Convergence Testing
      • Example Comparing Two Infinite Series
      • Convergence Test Videos
  • Unit 3: Power Series
    • Power Series
      • A Motivating Problem for Power Series
      • The Power Series
      • Power Series Example
      • Power Series Convergence
      • Power Series Convergence Example
      • Videos on Power Series
    • Taylor Series
      • A Motivating Problem
      • The Taylor Series
      • Maclaurin Expansion of ex
      • Maclaurin Expansion of sin(x)
      • The Maclaurin Expansion of cos(x)
      • List of Maclaurin Expansions
      • Videos on Taylor Series
• Appendices
  • Recommended Textbooks and Course Notes
  • The Contrapositive and the Divergence Test
    • The Definition of the Contrapositive
    • Contrapositive Examples
    • Contrapositive Example with Sets
    • Back to The Divergence Test
  • Proof of the Ratio Test
    • Absolute Convergence
    • Absolute Convergence Implies Convergence
    • Proof of the Ratio Test
  • List of Videos in the ISM
• Download
• Quizzes
  • Quiz 1
  • Quiz 2
  • Quiz 3
• Contact

Changing Summation Limits

[previous] [next]

In some cases we need to find an equivalent representation of a given summation, but that has different summation limits. For example, we may need to find an equivalent representation of the following sum

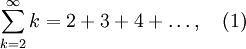
where the index of summation start at 1 instead of 2. We will introduce two methods for doing this.

Method 1

Introducing the transformation 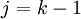, so that when k = 2, j = 1, yields

as desired. The summation index now starts at 1 instead of at 2.

Method 1 Observations

If we like, we can go back to calling our summation index k,

because it does not matter what we call our index. Also observe that the transformation 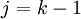was chosen so that our new index of summation, , starts at 1. You will also notice that although we accomplished our task, the general term was transformed from k to k + 1. This may not be what we need in certain problems, as we will see in other lessons within this Unit. Method 2 requires more work, but circumvents this problem.

Method 2

Now suppose we would like to

• re-write the sum so that we have the index of summation start at 1, but
• not change the general term.

Instead of using a change of variable, we can use another trick to accomplish this task.

Our procedure is to add and subtract terms in the sum to shift our index to 1:

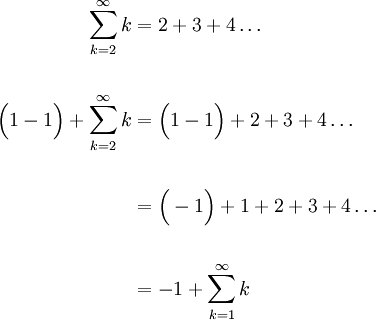
Therefore,

as desired. Using Method 2, the general term (in this example the general term is k) has not changed.

If you find this process confusing or wonder why we would need to use it, fear not. We will go through another example in more detail, and additional lessons in this unit make use of this method.

[previous] [next]

Leave a Reply Cancel reply

You must be logged in to post a comment.

• Search for:

• Site Map

  • Home
  • About the ISM
  • Units
    • Unit 1: Sequences and Series
      • Infinite Sequences
      • Sigma Notation
        • Introduction to Sigma Notation
        • Sigma Notation Terminology
        • Sigma Notation Properties
        • Changing Summation Limits
        • Example: Changing the Summation Limits
        • Videos on Sigma Notation
        • Final Thoughts on Sigma Notation
      • Infinite Series
      • Properties of Convergent Series
      • The Telescoping and Harmonic Series
    • Unit 2: Convergence Tests
    • Unit 3: Power Series
  • Appendices
  • Download
  • Quizzes
  • Contact

• The Infinite Series Module by The University of British Columbia Mathematics Department is licensed under a Creative Commons Attribution-ShareAlike 2.5 Canada License, based on a work at blogs.ubc.ca/infiniteseriesmodule/.Additional copyright information regarding the ISM is available here.

• Contact

• Website Technical Requirements

The Infinite Series Module Proudly powered by WordPress.

Spam prevention powered by Akismet