Collinear Points: Formulas, Definition, Sample Questions

Collegedunia.com4.61M+ DownloadsInstall AppMenuWrite a Review & Get upto ₹300*Select Your GoalSelect GoalBrowse Categories

No course found

All CoursesHelpful For Your Career Course FinderCollege PredictorScholarshipsEducation LoanAsk a QuestionTest SeriesPractice QuestionsRead College ReviewsStudy AbroadCountriesAbroad ExamsOther Popular LinksWrite a reviewNewsAdmissions 2026Top CoursesInstituteStudy AbroadTop Universities & CollegesScholarshipsExamsTop CouponsProfileWrite a Review & Get upto ₹300*Hello, Welcome To CollegeduniaSearch Colleges, Exams, Courses & MoreSelect GoalLogin/Register Now

1. >Exams
2. >Class 9
3. >Mathematics
4. >Lines and Angles

Collinear Points: Definition, Formula & Solved Examples

Collegedunia Team

Content Curator

×

Collinear points are three or more points that lie on the same straight line. The word ‘Collinear’ is a compound word that is made of two words: ‘co’ meaning togetherness and ‘linear’ meaning a line. Collinear points might exist on different planes but not on different lines. Since the points are collinear, it is known as collinearity. Non-collinear points are points which do not lie on a straight line. 

Collinear points applications in real life include, students standing in a straight line in an assembly, cars parked on a straight line in the parking lot or a set of balls kept on a straight line. Collinear Points are important in solving real life problems from Euclidean Geometry. Only one straight line can be drawn from a pair of say 3 collinear points. The collinear point formula can be estimated using method of slope, area of triangle or the distance formula. 

Read More:  NCERT Solutions Class 9 Maths

Table of Content Collinear Points Collinear Points in Maths Formulas of Collinear Points Non-Collinear Points Solved Examples Things to Remember Sample Questions

Key Terms: Collinear, Collinearity, Straight Lines, Points, Geometry, Collinear Point Formula, Slope, Area of Triangle, Distance, Non-Collinear

Collinear Points

[Click Here for Sample Questions]

When three or more points lie on the same straight line on a given plane, they are known as Collinear points. These points are aligned in a row or a line. Real-life collinear points include people standing in queue, and bottles kept in a row in the fridge.

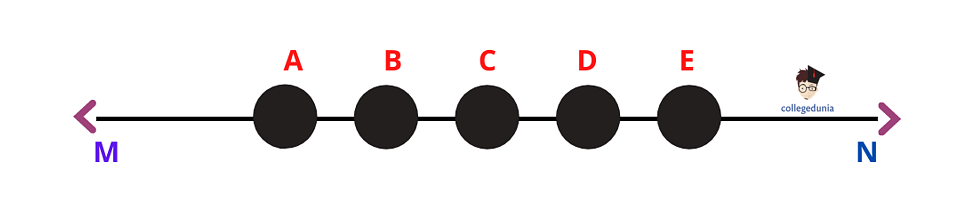
Collinear Points

The video below explains this:

Collinear Point Formulae Detailed Video Explanation:

Also Read: Intersecting & Non-Intersecting Lines

Collinear Points in Maths

[Click Here for Sample Questions]

In Mathematics, Collinear Points are points that are positioned on the same straight line. In the figure below, points (A, B, C,D, E) and points (I, H, C, F, G) are collinear.

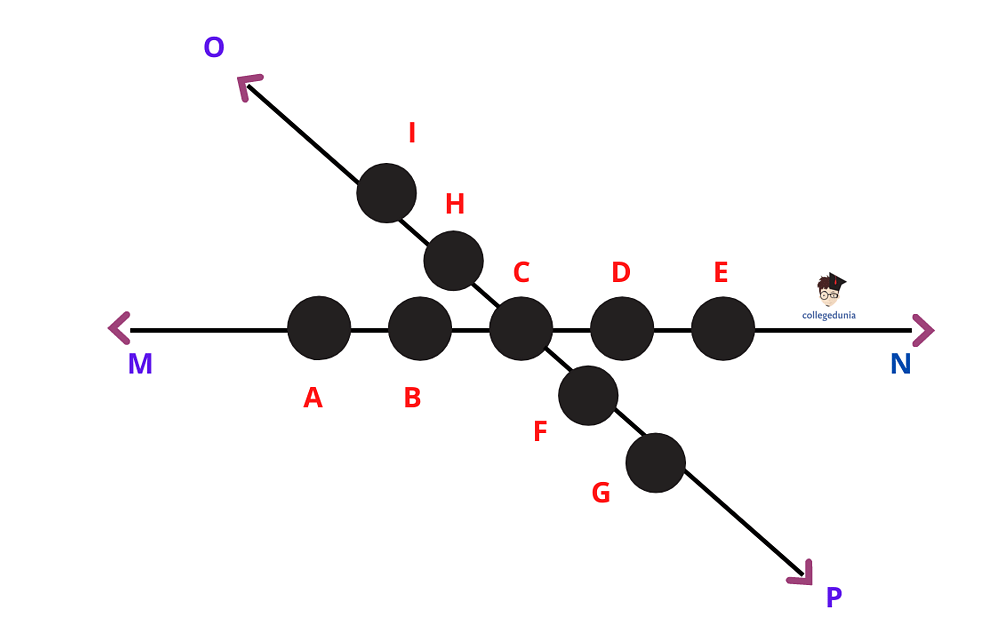
Collinear Points in Maths

Do Check Out:

Important Concepts Related to Collinear Points
Distance between Two Points	Horizontal and Vertical Lines	Lines and Angles
Vertex	Transversal	Properties of Parallel Lines
Angle Formula	Obtuse Angle	Linear Pair of Angles

Formulas of Collinear Points

[Click Here for Sample Questions]

There are three basic ways of finding if three points are collinear or not.

Slope Formula Method

If the slope of any two pairs of points is the same, then the three points are definitely on the same line and they are collinear.

For example, Imagine there are three points- A, B, and C. So the pairs are AB, BC, and AC.

So, if Slope of AB= Slope of BC, then A, B, and C are collinear points.

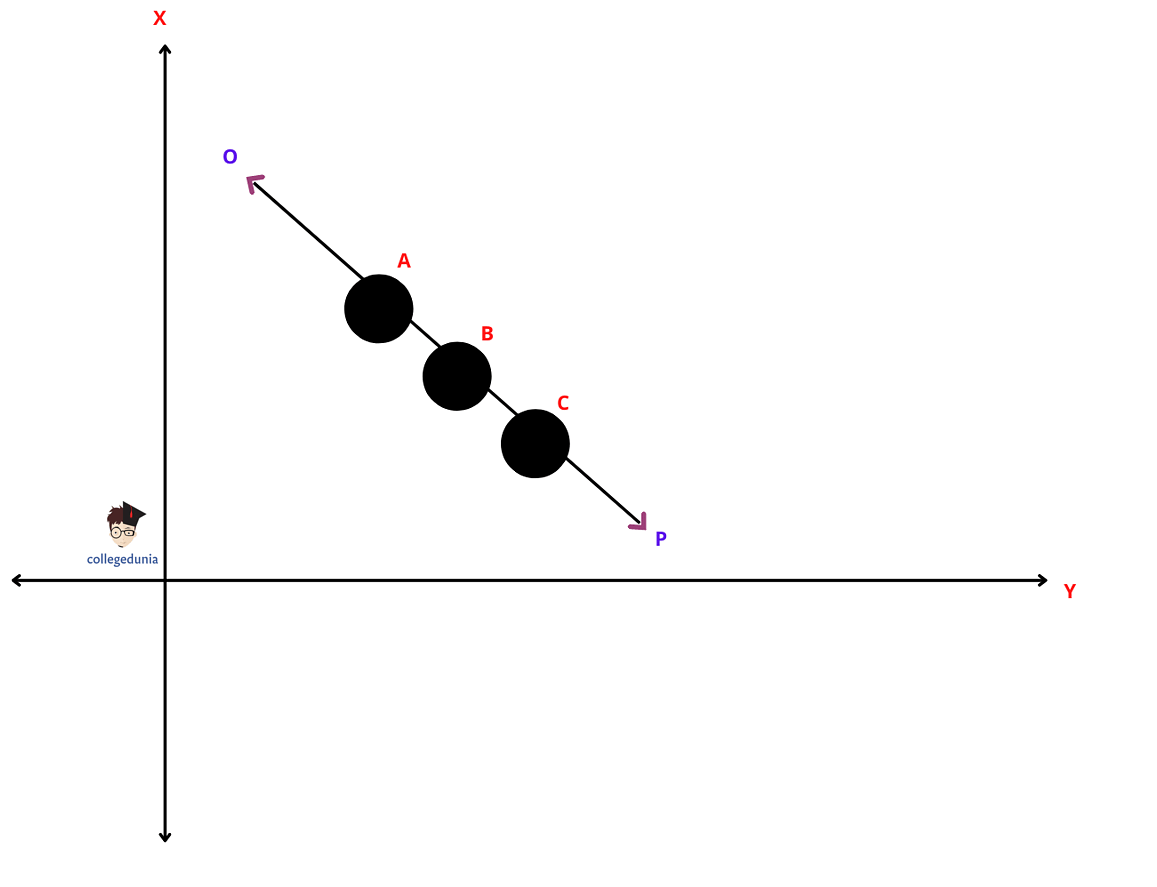
Slope Formula Method

Also Read: Three Dimensional Geometry

Area of the Triangle Method

Another method to prove whether the points are collinear points or not is by finding the area of the triangle formed by the three points. If the area is 0, the points are collinear.

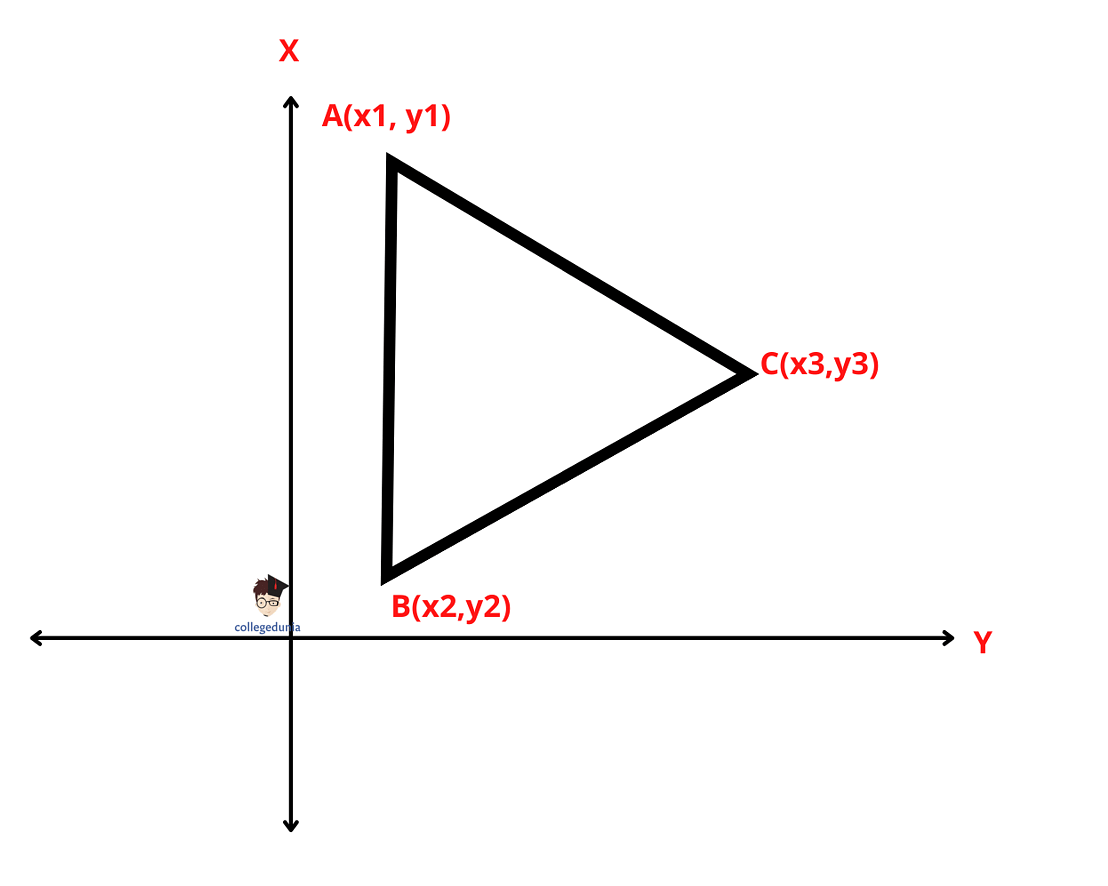
Area of the Triangle Method

For Example,The three points A(x1, y1), B(x2, y2), and C(x3, y3) are collinear, then by remembering the formula of area of the triangle formed by three points we get;

(1/2) | [x1(y2 – y3) + x2(y3 – y1) + x3[y1 – y2]| = 0

Also Read: Lines and Angles MCQs

Distance Method

If the distance between the 1st point and 2nd point added to the distance between 2nd point and 3rd point is equal to the distance between 1st and 3rd point, then all the three points are collinear.

For example, If we take A, B, and C as any three collinear points, then,

Distance from A to B + Distance from B to C = Distance from A to C

So, A, B and C are collinear points

Now, by the distance formula we know, the distance between two points (x1, y1) and (x2, y2) is given by;

D=√(x2−x1)2+(y2−y1)2

Non-Collinear Points

[Click Here for Sample Questions]

Points that are not on the same line and through which a straight line can never be formed, are known as non-collinear points.

For Example, Let consider the following figure, we cannot draw lines combining the points P, Q, R, S & T. Thus, they are non-collinear points.

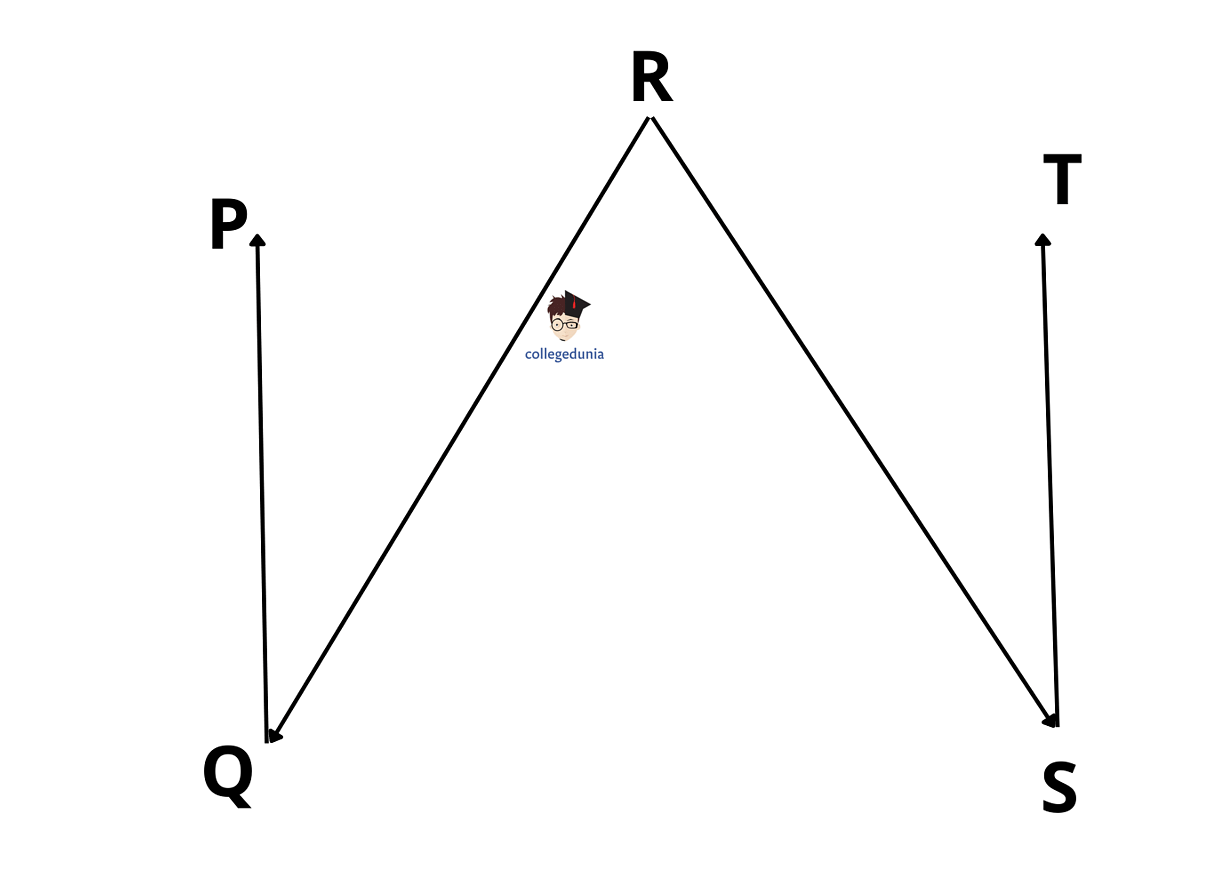Non-Linear Points

Also Read: Corresponding Angles Axiom

Solved Examples Ques: Prove that points A(5, -2), B(4, -1) and C(1, 2) are collinear points using the Distance Method. Solution : Distance between any two points (x1, y1) and (x2, y2) is  d = √[(x2 - x1)2 + (y2 - y1)2] To find the lengths AB, BC and AC using the formula, AB = √[(4 - 5)2 + (-1 + 2)2] AB = √[(-1)2 + (1)2] AB = √[1 + 1] AB = √2 BC = √[(1 - 4)2 + (2 + 1)2] BC = √[(-3)2 + (3)2] BC = √[9 + 9] BC = √18 BC = 3√2 AC = √[(1 - 5)2 + (2 + 2)2] AC = √[(-4)2 + (4)2] AC = √[16 + 16] AC = √32 AC = 4√2 Therefore, AB + BC = √2 + 3√2 = 4√2 = AC Thus, AB + BC = AC This proves that given three points A, B, and C are collinear. Ques: Prove that the given three points (4, 4), (-2, 6), and (1, 5) are collinear points using Slope Formula Method. Solution: Formula: m = (y2 - y1)/(x2-x1) Step 1 : AB’s Slope : (x1, y1) ==> (4 , 4) and (x2, y2) ==> (-2 , 6) m = (6 - 4) / (-2 - 4) = 2/(-6) = -1/3 Step 2 : BC’s Slope : (x1, y1) ==> (-2, 6) and (x2, y2) ==> (1, 5) m = (5 - 6) / (1 - (-2)) = (-1 )/(1 + 2) = -1/3 Step 3 : Slope of ‘AB’ = Slope of ‘BC’ Hence, the given points are collinear

Things to Remember

• Three or more points lying on the same straight line are known as the collinear points.
• Points that are positioned at non-linear positions on which a straight line cannot be formed are known as non-linear points.
• There are three main ways of finding whether points are collinear or not.
• If three points are collinear, the slopes formed from any two points are the same as the slope formed by the other two.
• The area of the triangle formed by any three collinear points will always be zero.

Also Read: 

Important Concepts Related to Lines & Angles
Types of Vectors	Pascal’s Triangle	Angle between Line and Plane
Vectors	Angles between Two Lines	Equation of Plane
Addition of Vectors	Angles between Two Planes	Section Formula in Coordinate Geometry
Hyperbola	Distance Formula and Derivation of Coordinate Geometry	Standard Equation of a Circle
Conic Sections Parabola	Parabola	Latus Rectum of Hyperbola

Sample Questions

Ques. What are collinear points in Geometry? (1 Marks)

Ans: In Geometry, if three or more points are aligned on a straight line, then those points are collinear.

Ques. What is the meaning of the words ‘collinear’? (2 Marks)

Ans: The word collinear is a compound word that is composed of two Latin terms; ‘co’ meaning togetherness and ‘linear’ meaning line. So, collinear means together in a line.

Ques. Give some examples of non-collinear points? (2 Marks)

Ans: Few real-life examples of non-linear points are-

• Players scattered in the field during the match
• Scattered pieces in a carrom board

Ques. What is the formula of collinearity? (2 Marks)

Ans: The formula of collinearity is-

Three collinear points are A, B, and C, then, AB + BC = AC.. If the area is equal to zero, then the points will be collinear. For example, if three points A (a1, b1), B (a2, b2) and C (a3, b3) are collinear, then [a1(b2 - b3) + a2( b3 - b1)+ a3(b1 - b2)] = 0.

Ques. What is the difference between collinearity and coplanarity? (3 Marks)

Ans: Collinearity is the property of the three or more points which lie on the same straight line, whereas, Coplanarity is the property of the points which are positioned on the same plane.

Ques. Can collinear points be coplanar as well? (3 Marks)

Ans: Yes, we can consider collinear points to be coplanar as well. If the points are collinear then most necessarily positioned on any of the infinite numbers of planes. Hence, collinear points are coplanar, but coplanar points might or might not be collinear.

Ques. What are the three basic ways of proving collinear points? (3 Marks)

Ans: There are three ways of proving Collinear points-

• Area of the triangle method
• Distance method
• Slope formula method

Ques. What are some real-life examples of collinear points? (3 Marks)

Ans: Some of the real-life examples of collinear points are-

• Numbers on a ruler
• Commuters seated on a train
• Plants in one row in a garden
• Bottles in a row in the fridge
• Students of a class standing in a line during a school assembly

Do Check Out:

Important Study Guides
NCERT Solutions Class 6 to 12	Important Maths Formulas	Comparison Topics in Maths
Maths MCQs	Choice based questions in physics	NCERT Class 9 Maths Book
Physics Study Notes	Maths Study Material	NCERT Solutions Class 7 Maths
Important Derivations in Physics	SI units in Physics	Important Physics Constants and Units
NCERT Solutions Class 8 Maths	Topics for Comparison in Physics	Formulas in Physics
Periodic Table in Chemistry	Chemistry Study Notes	Important Chemistry Formulas
Comparison Topics in Biology	Important Chemical Reactions	Biology Study Notes
Important Named Reactions	Biology MCQs	Comparison topics in Chemistry
Chemistry MCQs	Topics with relation in physics	NCERT Class 9 Science Book

CBSE X Related Questions

• 1.Solve the following pair of linear equations by graphical method : \(2x + y = 9\) and \(x - 2y = 2\).

  View Solution

• 2.

  On the day of her examination, Riya sharpened her pencil from both ends as shown below. The diameter of the cylindrical and conical part of the pencil is 4.2 mm. If the height of each conical part is 2.8 mm and the length of the entire pencil is 105.6 mm, find the total surface area of the pencil.

  View Solution

• 3.A box contains 120 discs, which are numbered from 1 to 120. If one disc is drawn at random from the box, find the probability that (i) it bears a 2-digit number (ii) the number is a perfect square.

  View Solution

• 4.

  In the adjoining figure, $\triangle CAB$ is a right triangle, right angled at A and $AD \perp BC$. Prove that $\triangle ADB \sim \triangle CDA$. Further, if $BC = 10$ cm and $CD = 2$ cm, find the length of AD.

  View Solution

• 5.Prove that: \[ \frac{\cos \theta - 2 \cos^3 \theta}{\sin \theta - 2 \sin^3 \theta} + \cot \theta = 0 \]

  View Solution

• 6.If the points $A(6, 1)$, $B(p, 2)$, $C(9, 4)$ and $D(7, q)$ are the vertices of a parallelogram $ABCD$, then find the values of $p$ and $q$. Hence, check whether $ABCD$ is a rectangle or not.

  View Solution

View All

Similar Mathematics Concepts

Angle between two lines: Derivation, Types, Formulae Angle Formula: Definition, Different Types, Solved Example Corresponding Angles Axioms: Definition, Types and Sample Questions NCERT Solutions for Class 9 Maths Chapter 6 : Lines and Angles Lines and Angles: Types, Properties and Examples Acute Angle: Properties & Triangle Inequality Theorem Exterior Angle Theorem: Properties, Proof & Examples Lines and Angles MCQs Right Angle: Types, Parts & Geometric Construction Construction of Perpendicular Lines: Formula, Method, Sample QuestionsMathematics Preparation GuidesStatistics: Mean, Median, Variance and Cumulative Frequency CurveRemainder Theorem: Definition, Steps & ExamplesAngle Formula: Definition, Different Types, Solved ExampleTrapezoids: Isosceles, Scalene Properties, Area, Properties, ExamplesQuadrilateral Angle Sum Property: Theorem, Types & ExampleFrequency Polygons: Steps, Formula & ExamplesArea of Parallelogram: How to Calculate Area of Parallelogram?Congruence of Triangles: SSS, SAS, ASA & RHS RulesQuadrilateral Formulas: Types and PropertiesProperties of Triangle: Types, Formulas & ExamplesClass 9 Maths MCQ: Chapter-wise with SolutionsProperties of Parallel Lines: Transitive & Symmetric PropertiesIsosceles triangle: Types, Properties, Angles & ExamplesOperations on Rational Numbers:Rules, Properties & ExamplesAddition and Subtraction of Integers: Rules & ExamplesScalene Triangle: Types, Formulas, Properties & ExamplesQuadrant: Types, Sign Convention & ExamplesRationalize the Denominator: Explanation and Solved ExamplesArea of a Kite: Formula, Derivation & ExamplesVolume of a Pyramid: Formula and Solved ExampleMathematics NCERT SolutionsLinear Equation in Two Variables: Graph, Elimination and SubstitutionTypes of Triangles: Important Terms, Scalene, Acute, and Obtuse TriangleFormula Of Perimeter ShapesSphere Formula: Diameter, Surface Area and VolumeOrdinate: Abscissa, Plotting Ordinates, Relation, Solved ExamplesIntegers as Exponents: Explanation, Rules and Method of SolvingCentral Tendency: Definition, Methods and Sample QuestionsLine Segment: Definition, Measurement and ExamplesLine, Line Segment and Ray: Differentiation and Sample QuestionsArea of Equilateral Triangle, Perimeter & Altitude Formulas

Comments

No Comments To Show

Subscribe to Our News letter

Get latest notification of colleges, exams and news+91SUBMIT

• About Us
• Contact Us
• Advertising
• Careers
• Terms & Conditions
• Privacy Policy

© 2026 Collegedunia Web Pvt. Ltd. All Rights Reserved