Construction Of Angles - Using Protractor And Compass, Steps Of ...

Construction of Angles

The construction of angles is one of the most important aspects of geometry and is the "pure" form of geometric construction. The term construction in geometry refers to drawing shapes, lines, or angles accurately with the help of mathematical instruments. To construct angles, you will only need a pair of a compass or a protractor, a ruler (straightedge), and a pencil.

1.	Types of Angles
2.	Construction of Angles Using a Protractor
3.	Constructing Angles with Compass and Ruler
4.	FAQs on Construction of Angles

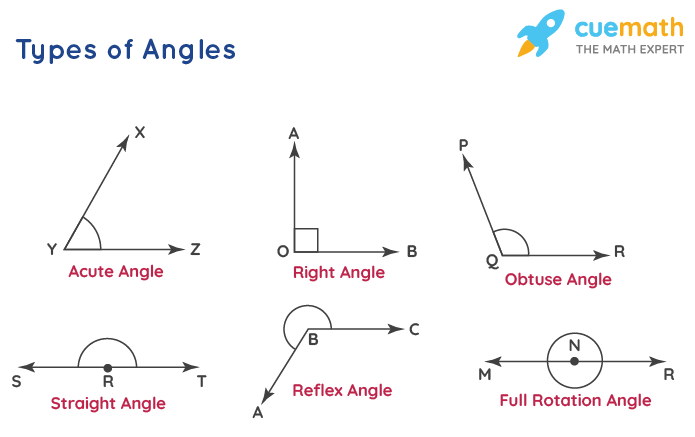
Types of Angles

When two lines intersect and have a common endpoint that is when an angle is formed. Learning about angles in geometry is very important. Below are the 6 types of angles in geometry along with the degree measurement of angles.

• Acute Angle→ An angle that measures less than 90°.
• Right Angle→ An angle that measures exactly 90°.
• Straight Angle→ An angle that measures equal to 180 degrees and looks like a straight line.
• Obtuse Angle → An angle that measures greater than 90° but less than 180°.
• Reflex Angle → An angle that always measures more than 180° (i.e. half a circle) but less than 360°.
• Full Rotation Angle → An angle that measures 360° exactly.

Constructing Angles Using a Protractor

An angle can be constructed either by using a protractor and a ruler or a compass and a ruler. Let us now look at the steps of constructing a 50° angle using a protractor.

• Step 1 - Draw a line segment OA.
• Step 2 - Place the center of the protractor at point O.
• Step 3 - Starting from point A in the clockwise direction and mark a point at 50 degrees by looking at the outer circle of the protractor. Label this point as B.

The ∠BOA is the required 50° angle.

Constructing Angles with Compass and Ruler

Let us learn how to construct an angle with a compass and a ruler. In the steps shown below we will be constructing an angle of 90° and then construct an angle bisector to bisect the 90° such that we will get an angle of 45°.

• Step 1: Draw a ray AB.
• Step 2: With A as the center and any width as radius draw a semicircular arc that touches the line segment AB and mark it as Q.
• Step 3: Without any change in radius, draw another arc with Q as the center and label this point as D.
• Step 4: Repeat the same process with D as the center and label the arc drawn as E.
• Step 5: Now, with the same radius and with E and D as centers draw arcs that intersect each other at a point and label it as F.
• Step 6: Now join the points A and F. This line is called the perpendicular line and it makes 90 degrees with the line segment AB.
• Step 7: Label the point of intersection of the semicircular arc with the line AF as P.
• Step 8: Now with the same radius taken to draw an arc in step 2, draw two arcs with P and Q as centers. Mark the point of intersection of these arcs as R. Now join the points A and R. Now ∠RAB and ∠FAR are equal to 45° each.

Topics Related to Construction of Angles

Check out some interesting articles related to the construction of angles.

• Constructing Angle Bisectors
• Geometric construction
• Pairs of Angles
• Angle Bisector
• Angles