Cross Multiplying Fractions (Video & Practice Questions) - Mometrix

Hey guys! Welcome to this video on how to cross multiply fractions.

When cross multiplying fractions, the name sort of hints at how this is actually done.

You literally multiply across. Let’s say you have two fractions that are set equal to each other. So let’s say, \(\frac{a}{b}=\frac{c}{d}\).

Well, to cross multiply them, you multiply the numerator in the first fraction times the denominator in the second fraction, then you write that number down. Then you multiply the numerator of the second fraction times the number in the denominator of your first fraction, and you write that number down.

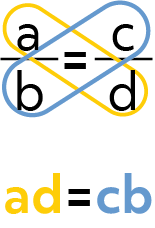
The reason we cross multiply fractions is to compare them. Cross multiplying fractions tells us if two fractions are equal or which one is greater. This is especially useful when you are working with larger fractions that you aren’t sure how to reduce.

How to Cross Multiply

Cross Multiply Fractions – Example 1

Find which of the two fractions is greatest.

\(\frac{4}{26}=\frac{7}{32}\) So, when we cross multiply it, when we set it equal, and then cross multiply these two fractions together, we get 128. So \(4\times 32=128\). And when we cross multiply these two, we get \(7\times 26=182\). So, we know that \(\frac{7}{32}\) is greater than \(\frac{4}{26}\) because 182 is greater than 128.

We must always remember that the number that we multiplied with our numerator represents that corresponding fraction. So this number (128) is representing this fraction \((\frac{4}{26})\), and this number (182) is representing this fraction \((\frac{7}{32})\). I mention this, because it may be a little confusing to see numbers taken from two different fractions being multiplied together, but the product only representing one of the fractions and not the other. 128 goes on the left side to represent \(\frac{4}{26}\) and \(7\times 26=182\) goes on the right side to represent this fraction right here \((\frac{7}{32})\).

Cross multiplying fractions helps us to see if numbers are equal, and if not, which is bigger and which is smaller. But that is not its only use. Cross multiplying fractions can help us to solve for unknown variables in fractions.

Cross Multiply Fractions – Example 2

Let’s say we have two fractions \(\frac{9}{16}=\frac{x}{27}\). We can cross multiply anytime we have a fraction that is set equal to another fraction. Now, to cross multiply we do the exact same thing that we did in our last example. We take the numerator of one side and multiply it times the denominator of the other side, and do this same the from the numerator of the other side. In this case, we multiply \(9\times 27\) and \(16\times x\). This would give us \(243=16x\). Now, all we have to do to get x by itself is divide both sides by 16. This cancels out, and this gives us \(x=\frac{243}{16}\), and you can simplify this even further. Now, we would do this exact same thing even if \(x\) is in our denominator, it doesn’t matter.

I hope that this video over cross multiplying fractions has been helpful to you.

See you guys next time!

Adding and Subtracting Fractions | Multiplying and Dividing Fractions