Equilateral Triangles Calculator

Equilateral Triangle Shape

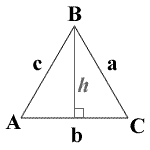A = angle A a = side a B = angle B b = side b C = angle C c = side c A = B = C = 60° a = b = c K = area P = perimeter s = semiperimeter h = altitude

*Length units are for your reference only since the value of the resulting lengths will always be the same no matter what the units are.

An equilateral triangle is a special case of a triangle where all 3 sides have equal length and all 3 angles are equal to 60 degrees. The altitude shown h is hb or, the altitude of b. For equilateral triangles h = ha = hb = hc.

If you have any 1 known you can find the other 4 unknowns. So if you know the length of a side = a, or the perimeter = P, or the semiperimeter = s, or the area = K, or the altitude = h, you can calculate the other values. Below are the 5 different choices of calculations you can make with this equilateral triangle calculator. Let us know if you have any other suggestions!

Formulas and Calculations for a equilateral triangle:

• Perimeter of Equilateral Triangle: P = 3a
• Semiperimeter of Equilateral Triangle: s = 3a / 2
• Area of Equilateral Triangle: K = (1/4) * √3 * a2
• Altitude of Equilateral Triangle h = (1/2) * √3 * a
• Angles of Equilateral Triangle: A = B = C = 60°
• Sides of Equilateral Triangle: a = b = c

1. Given the side find the perimeter, semiperimeter, area and altitude

• a is known; find P, s, K and h
• P = 3a
• s = 3a / 2
• K = (1/4) * √3 * a2
• h = (1/2) * √3 * a

2. Given the perimeter find the side, semiperimeter, area and altitude

• P is known; find a, s, K and h
• a = P/3
• s = 3a / 2
• K = (1/4) * √3 * a2
• h = (1/2) * √3 * a

3. Given the semiperimeter find the side, perimeter, area and altitude

• s is known; find a, P, K and h
• a = 2s / 3
• P = 3a
• K = (1/4) * √3 * a2
• h = (1/2) * √3 * a

4. Given the area find the side, perimeter, semiperimeter and altitude

• K is known; find a, P, s and h
• a = √ [ (4 / √3) * K ] = 2 * √ [ K / √3 ]
• P = 3a
• s = 3a / 2
• h = (1/2) * √3 * a

5. Given the altitude find the side, perimeter, semiperimeter and area

• h is known; find a, P, s and K
• a = (2 / √3) * h
• P = 3a
• s = 3a / 2
• K = (1/4) * √3 * a2

For more information on triangles see:

Weisstein, Eric W. "Equilateral Triangle." From MathWorld--A Wolfram Web Resource. Equilateral Triangle.

Weisstein, Eric W. "Altitude." From MathWorld--A Wolfram Web Resource. Altitude.