Error Bars -- Frequently Used But Rarely Questioned

Home » What Does It Mean When Error Bars Overlap » Error Bars -- Frequently Used But Rarely Questioned

Maybe your like

Skip to content
  • Post author:Dr. Mario Schneider

I have seen many publications with beautiful colored graphs including well-formatted error bars. Unfortunately, a lot of these publications do not state what these error bars represent. If not stated in the figure’s caption, one starts to look at the main text. In the worst case it is not even stated there. If the data points are plotted in the same graph, one can sometimes guess what type of error bars might be shown, but if the data is missing, this becomes difficult. It might seem tempting to use those types that are very narrow, e.g. use standard error bars instead of standard deviations (for the difference between the different types of error bars, please go on reading) but the choice of the error bar type should depend on what you want to show with your data. Often, it is even better to leave error bars completely aside and simply plot the data points. If you choose to plot error bars keep in mind that there are various ways to do so. The most common error bar types are those derived from standard deviations (SD), standard errors (SE) or confidence intervals (CI). The SD is a typical measure of the scatter in the data set and can be viewed as the average distance of the data points from the mean. Increasing the sample size will not narrow SD error bars (of course, the sample standard deviation will be a better estimate for the true SD for larger sample sizes). When comparing two group means, do not use SD error bars. It is a misconception to think that the two group means are significantly different if the SD error bars do not overlap. In general, this is not true. Nevertheless, non-overlapping SD error bars can be regarded as a positive sign if you aim for a significant difference of the means in practice. It is also not true that overlapping SD error bars indicate a non-significant difference. Only an appropriate significance test (e.g. Student’s t-test) might reveal statistical significance. Error bars based on the SE or based on CIs are sample size-dependent. The SE denotes the standard deviation of the mean, of some fit parameter or some other derived statistical quantity and is simply the sample standard deviation divided by the square root of the number of data points. Increasing the number of data points thus decreases the standard error and narrows the corresponding error bars (see Figure 1).

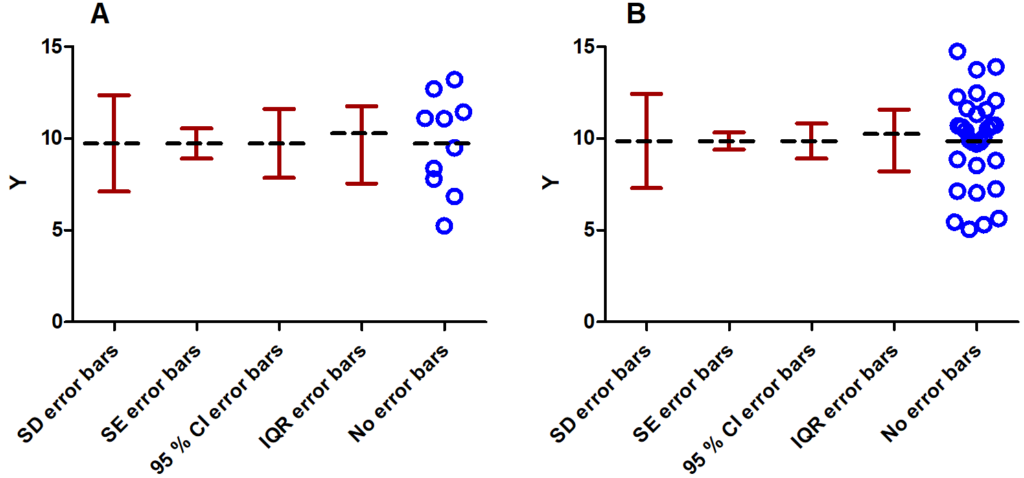
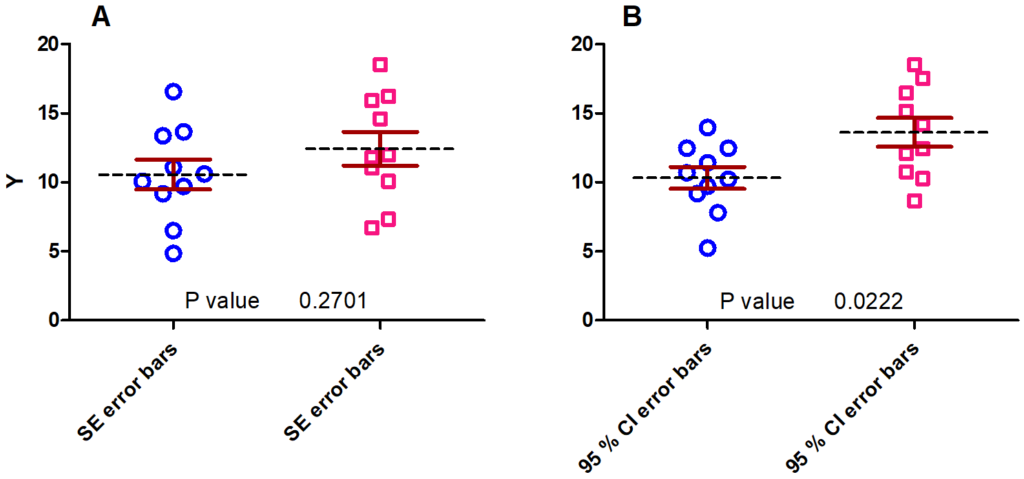
Comparison of different error bar types applied to a data set with (A) N=10 and (B) N=30 data points. The dashed lines indicate the mean of the data (median in case of IQR error bars).

I saw students using SE instead of SD error bars only because the former ones were narrower. However, this is not the right reason to use them. They might be used to compare two or more data sets for inferential purposes. As a rule of thumb: If two data sets have comparable sample sizes and if the SE error bars of the two groups overlap then the two means cannot be considered significantly different. In general, if the SE error bars do not overlap one cannot say that the group means are significantly different. However, with CI error bars this statement can be made (at least for comparable sample sizes of the two data sets). If the CI error bars do not overlap, the group means are significantly different. Figure 2 gives an example for both the overlapping SE error bars (A) and non-overlapping 95 % CI error bars (B) with their corresponding p-values near the x-axis. To be on the safe side in practice, I recommend performing the appropriate hypothesis test such as the Student’s t-test or a one-way ANOVA in order to assess statistical significance and the corresponding p-value.

Just overlapping SE error bars leading to a p-value that indicates that the corresponding mean values (dashed lines) are not significantly different (at least for α=0.05). (B) Just non-overlapping 95 % CI error bars. The p-value indicates that there is a significant difference (at least for α=0.05) between the mean values (dashed lines).

When looking at Figure 1 and Figure 2, one might come to the conclusion that all error bars are symmetric. Nevertheless, looking closer at Figure 1 reveals that the interquartile range (IQR) error bars are not. Symmetric error bars suggest a symmetric underlying distribution. However, e.g. if the data follows a lognormal distribution rather than a normal distribution, it might make more sense to use the geometric SD instead of the normal SD for the error bars since the former one resembles the dispersion of the data better. Instead of being added (upper whisker) or subtracted (lower whisker) from the mean, the geometric SD is multiplied (upper whisker) or divided (lower whisker) from the geometric mean and can thus appear asymmetric on a linear scale.

To summarize, it is worth thinking about if error bars shall be plotted at all and if yes, which type of error bars shall be used. SD, quartiles or other descriptive measures error bars might be used to demonstrate the dispersion of the data while SE error bars and confidence intervals might be used for assessing significant differences between groups.

Tags: confidence interval, Error bars, inference, quartiles, standard deviation, standard error, whisker

Read more articles

Next PostConfidence and Prediction bands in Regression analysis

Dr. Mario Schneider

As an analytical chemist and certified AI Manager with a PhD in biophysics, Mario brings a unique blend of scientific rigor and strategic thinking to your business. His dedicated expertise in chemometrics and scientific data analysis allows him to turn your most complex data into clear, valuable insights. He is a published author on data analysis for scientists and a master of tools like MATLAB, R, Excel, and Python. Mario doesn't just process data; he leverages cutting-edge machine learning algorithms to uncover hidden opportunities, optimize processes, and drive innovation.

You Might Also Like

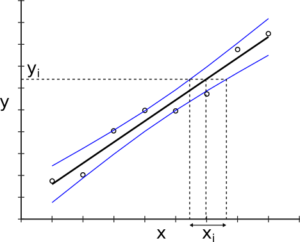
Read more about the article Confidence and Prediction bands in Regression analysis

Confidence and Prediction bands in Regression analysis

17. August 2020

Leave a Reply Cancel reply

CommentEnter your name or username to commentEnter your email address to commentEnter your website URL (optional)

Save my name, email, and website in this browser for the next time I comment.

By using this form, you consent to the storage and processing of your data by this website. *

News

New Online Course Cells-and-box-plot-and-gaussian-distribution

Enroll to our new online course: Data Analysis for Life Scientists

German data analysis video tutorials now on YouTube We are happy to announce that we have recently published our YouTube channel ‘data analysis for scientists’ together with Mario’s former chemometrics professor Dr. Ernst Cleve.

To the YouTube channel website

Book on data analysis was recently published. Mario has recently published his book on data analysis for scientists and engineers. For more details see our recent blog post.

To the book presentation

Recent Posts

  • Finding roots and Hunting for an Optimum
  • Bacteria and Their Most Probable Mumber (MPN)
  • Analysis of Bioassays
  • Weighted Regression — Is it cheating?
  • How to use Excel’s LAMBDA Function for Data Analysis?

To get a quote, please fill out this form.

Your Name (required) Your E-Mail-Address (required) Your Message By using this form, you consent to the storage and processing of your data by this website (required).

For more details view our privacy policy.

 Bitte lasse dieses Feld leer.

X

To get a quote, please fill out this form.

Your Name (required) Your E-Mail-Address (required) Your Message By using this form, you consent to the storage and processing of your data by this website (required).

For more details view our privacy policy.

 Bitte lasse dieses Feld leer.

X This website uses cookies. If you continue to use the website, we assume your consent.OKNoView Privacy Policy

Tag » What Does It Mean When Error Bars Overlap