Find Orthocenter Of Any Triangle - Calculator

An online Orthocenter Calculator helps you calculate the orthocenter of a triangle easily. This tool provides the exact coordinates of the orthocenter in seconds. Let’s explore the concept of the orthocenter in trigonometry.

What is Orthocenter?

The orthocenter of a triangle is the point where the altitudes of the triangle intersect, also called the point of concurrency.

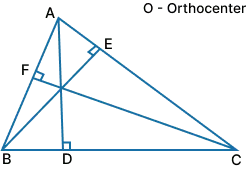
In the figure above, AB, BC, and CA are the sides of the triangle, and their corresponding altitudes are CF, AD, and BE. An altitude is a perpendicular line drawn from a vertex to its opposite side. The intersection point of all altitudes is the orthocenter, whose coordinates can be calculated quickly using an orthocenter calculator.

Properties of the Orthocenter

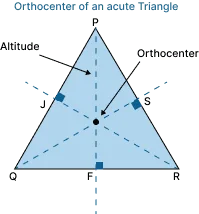
Orthocenter of an Acute Triangle:

An acute triangle has all angles less than 90°. The orthocenter of an acute triangle lies inside the triangle.

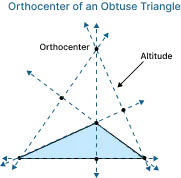
Orthocenter of an Obtuse Triangle:

An obtuse triangle has one angle greater than 90°. The orthocenter of an obtuse triangle lies outside the triangle.

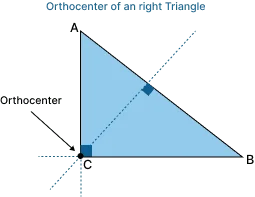
Orthocenter of a Right Triangle:

For a right triangle, the orthocenter lies on the vertex of the right angle.

Algebraic Formulas to Calculate Orthocenter

To find the orthocenter, we use slopes and equations of altitudes:

1. Slope of a side:

m = (y2 - y1) / (x2 - x1)

2. Slope of perpendicular (altitude):

m_perpendicular = -1 / m

3. Equation of an altitude:

y - y1 = m_perpendicular * (x - x1)

Solving these equations simultaneously gives the coordinates of the orthocenter.

Example: Find the Orthocenter

Vertices of the triangle: A(2, -3), B(8, -2), C(8, 6)

Step 1: Slope of AC:

m_AC = (6 - (-3)) / (8 - 2) = 9 / 6 = 3/2

Step 2: Slope of altitude BE:

m_BE = -1 / (3/2) = -2/3

Step 3: Equation of altitude BE through B(8,-2):

y + 2 = (-2/3)(x - 8)

3(y + 2) = -2(x - 8)

3y + 6 = -2x + 16 → 2x + 3y - 10 = 0

Step 4: Slope of BC:

m_BC = (6 - (-2)) / (8 - 8) = 8 / 0 → undefined

Step 5: Slope of altitude AD through A(2,-3):

m_AD = 0 (perpendicular to vertical line)

Equation of AD: y + 3 = 0 → y = -3

Step 6: Solve for x:

2x + 3(-3) - 10 = 0 → 2x - 9 - 10 = 0 → 2x = 19 → x = 19/2 = 9.5

Result: Orthocenter = (9.5, -3)

How Orthocenter Calculator Works

Input:

• Enter the coordinates of all vertices.
• Click 'Calculate'.

Output: The calculator gives the exact coordinates of the orthocenter with step-by-step solution.

FAQs

Is there a different method to find the orthocenter for various triangles?

No. The method is the same regardless of the triangle type.

Is there any triangle without an orthocenter?

No. Every triangle has an orthocenter, as it is the intersection of altitudes.

What does the orthocenter indicate?

The orthocenter indicates the point of concurrency of a triangle’s altitudes.

What is Euler’s Line?

Euler’s Line passes through several important triangle centers, including the orthocenter, centroid, and circumcenter.

Conclusion

The orthocenter is a key point of intersection in any triangle. Its position helps understand the triangle’s type. An orthocenter calculator quickly determines the coordinates with precision, making it useful for students and engineers alike.

References

Wikipedia: Orthocenter

Khan Academy: Common orthocenter and centroid

Lumen Learning: Rectangular Coordinate Systems and Graphs