Finding The Volume And Surface Area Of A Pyramid (Video & Practice)

Hello, and welcome to this video about pyramids! In this video, we will explore different types of pyramids and how to calculate their volume and surface area. Let’s learn about pyramids!

Historical Pyramids

We cannot talk about pyramids without mentioning the most famous pyramids in the world, located in Egypt, and built as a tomb for Egyptian kings. Although pyramids are not quite common, their shape is so striking that it seems it is used to make a statement, perhaps that is the reason the Egyptian kings used it as their tomb. The Louvre Museum in Paris, which is the largest art museum in the world, is also shaped like a pyramid.

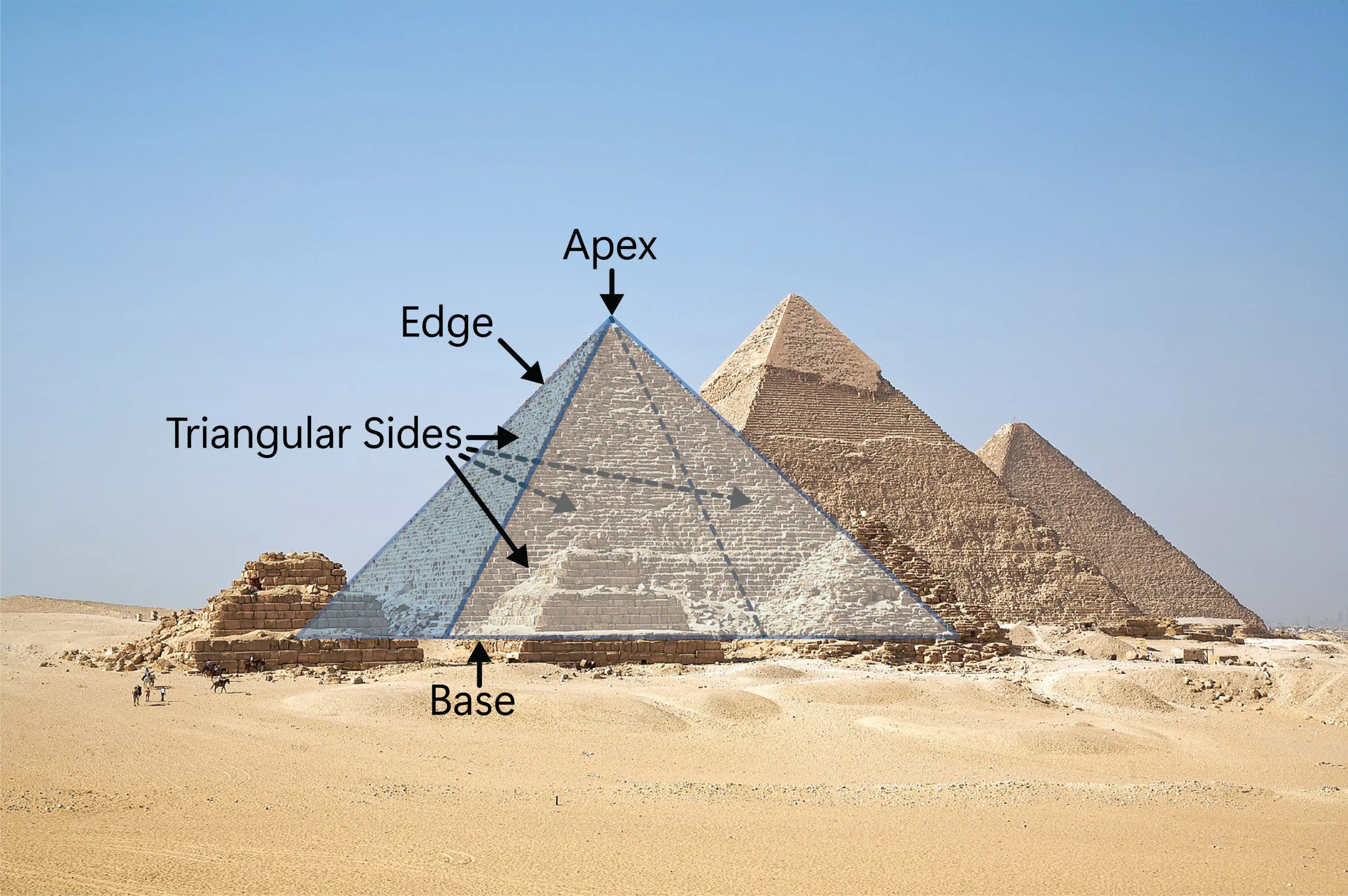
Pyramids in Geometry

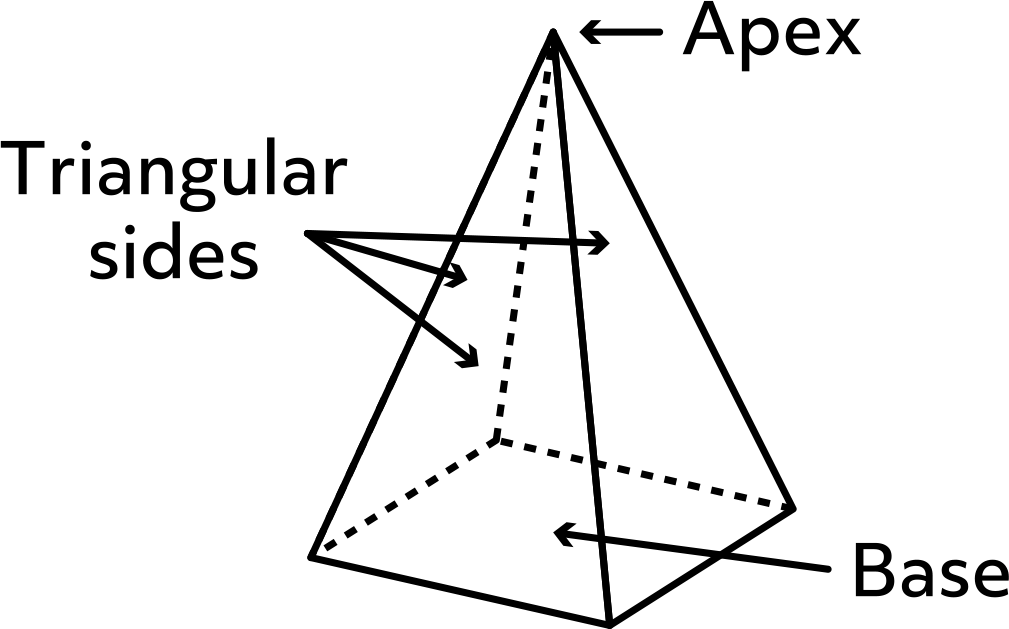
As you can see from the images of the Egyptian Pyramids, a pyramid is a 3-dimensional figure with triangular sides that meet at the edges and at the top to form an apex and it has a polygon as its base.

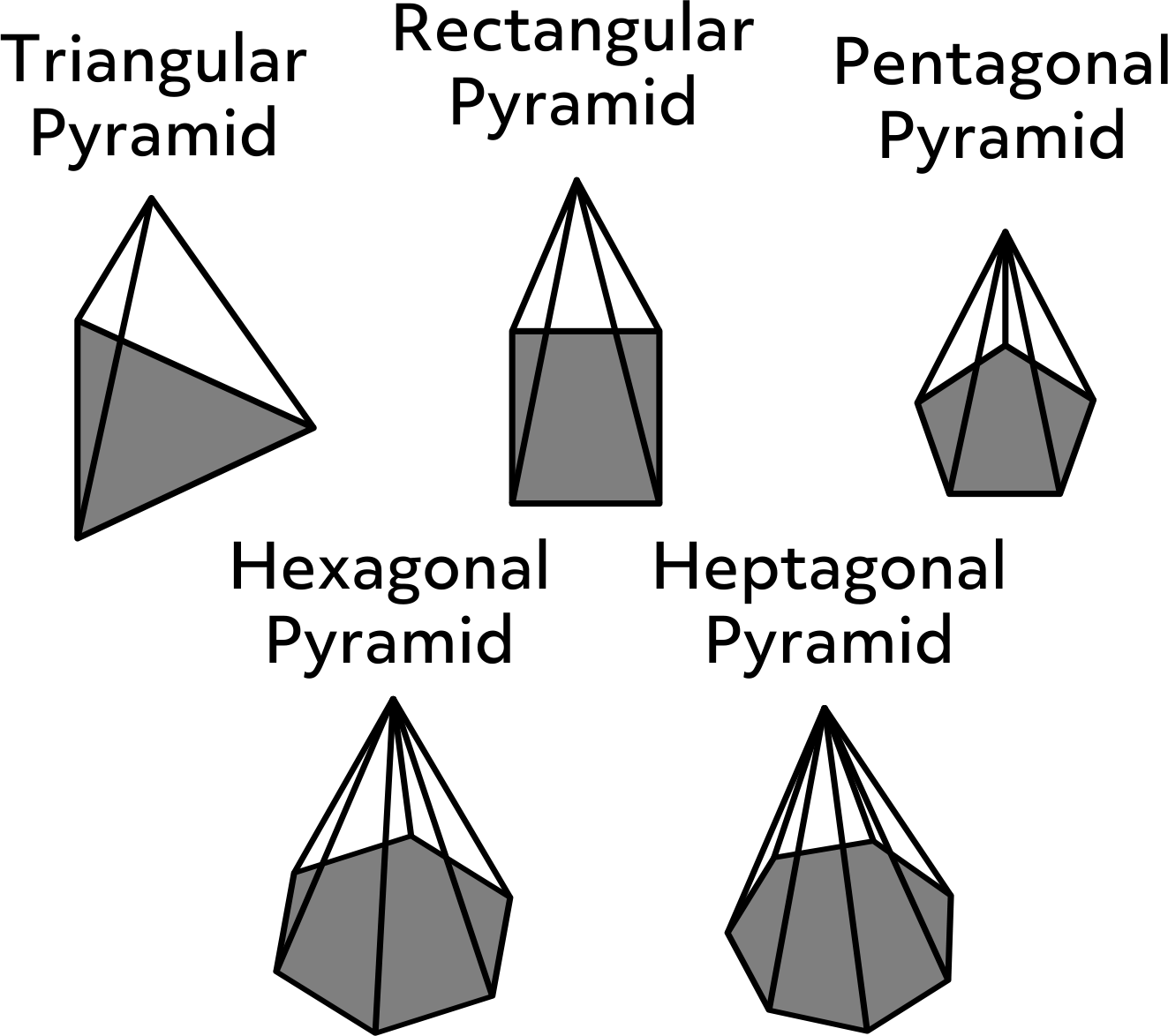
The polygonal base determines the type of pyramid. Here you see the pyramid with a triangle as its base is a triangular pyramid, the pyramid with a rectangle as its base is a rectangular pyramid, and the pyramid with a pentagon as its base is a pentagonal pyramid. We also have hexagonal pyramids and heptagonal pyramids, and so on.

Let’s take a moment and recall what the volume and surface area of a 3-dimensional figure means.

Volume and Surface Area Formula

The volume of a 3-dimensional figure is the measure of how much it can hold, and it is measured in cubic units.

The surface area of a 3-dimensional figure is the measure of the total area that the surface of the figure covers and is measured in square units.

Before we can calculate the volume and surface area of a pyramid, we must know the difference between the height and slant height. The height of a pyramid is the perpendicular length from the apex to the base, and the slant height is the length from the apex to the midpoint of the bottom edge of one of the triangular faces.

Here are the formulas for the volume and surface area of any pyramid.

\(V=\frac{1}{3}Bh\) \(SA=B+\frac{1}{2}ps\)

To calculate the volume and surface area of any pyramid we need B, which represents the area of the base, and p, which represents the perimeter of the base. It is important to note, since the base of a pyramid can be any polygon, we will be using our prior knowledge of finding the area and perimeter of different polygons to calculate the volume and surface area of a pyramid.

\(V=\frac{1}{3}Bh\) \(SA=B+\frac{1}{2}ps\)\(B\) = area of base \(h\) = height of pyramid \(p\) = perimeter of base \(s\) = slant height

Let’s look at an example.

Calculating Surface Area – Example 1

A triangular pyramid has an equilateral triangle as its base with side lengths 6 in and a height of 8 in.

To find the surface area of a pyramid, we use the formula \(SA=B+\frac{1}{2}ps\), where \(B\) is the area of the base, \(p\) is the perimeter of the base, and \(s\) is the slant height. Since the base is a triangle, we will use the formula for the area of a triangle to find \(B\).

\(\text{Area of a triangle}=\frac{1}{2}bh\), where the \(b\) and \(h\) are the base and height of the triangular base. We will draw a perpendicular line to the base, which is the height of the triangular base and it divides the base of the triangle into 2 equal parts. Since the triangle is now turned into 2 right triangles, we can use the Pythagorean theorem to find the height.

So the Pythagorean theorem is:

\(c^{2}=a^{2}+b^{2}\)

And then we’re gonna look at our triangle, which says we have:

\(6^{2}=h^{2}+3^{2}\) \(36=h^{2}+9\)

We’ll subtract 9 from both sides. This gives us:

\(27=h^{2}\)

And then we’ll square root both sides. Which gives us:

\(h=3\sqrt{3}\) OR \(h\approx 5.2\)

Therefore, the area of the base can be found by doing:

\(A=\frac{1}{2}bh\) \(A=\frac{1}{2}(6)(5.2)\) \(A\approx 15.6 \text{ in}^{2}\)

The perimeter of the base is equal to all the sides added together, so:

\(p=6+6+6=18\text{ inches}\)

Now to solve for surface area, all we have to do is plug these values in for our variables. So our surface area is equal to:

\(SA=B+\frac{1}{2}ps\) \(SA=(15.6)+\frac{1}{2}(18)(7)\) \(SA\approx 78.6 \text{ in}^{2}\)

And all this added together is approximately equal to 78.6 square inches.

Calculating Volume – Example 1

To find the volume of the triangular pyramid, we need the area of the base, \(B\), and the height of the pyramid, which is 8 inches. So let’s plug this in. So:

\(V=\frac{1}{3}Bh\) \(V=\frac{1}{3}(15.6)(8)\)

Now all we have to do is calculate this out, which is equal to approximately 41.6 cubic inches.

\(V=41.6\text{ in}^{3}\)

Let’s look at another example.

Calculating Volume – Example 2

Here is a pyramid with a square base, with side lengths of 5 centimeters. The height of the pyramid is 11 centimeters. What is the volume of the pyramid?

So our volume formula is:

\(V=\frac{1}{3}Bh\)

Before we can calculate the volume of the pyramid, we need to find the area of the base. Since the base is a square, we use the formula for the area of a square, which is \(s^{2}\). So to find our area, we’re gonna use \(s^{2}\) and our side length is 5.

\(A=s^{2}\) \(A=(5)^{2}\) \(A=25\text{ cm}^{2}\)

Now we can plug this value into our formula.

\(V=\frac{1}{3}Bh\) \( V=\frac{1}{3}(25)(11)\) \(V\approx 91.67\text{ cm}^{3}\)

Then if we plug this into a calculator, we’ll get that it’s approximately equal to 91.67 cubic centimeters.

But when would we ever need this in real life? Well, I’m glad you asked! Take a look at this next example and try it on your own.

Calculating Surface Area – Example 2

The roof of a wooden cottage is shaped like a square-based pyramid. The length of the sides of the square base are 22 feet and the height of the triangular face is 14 feet. Peter wants to paint the roof of his wooden cottage and needs to determine how much paint he needs to buy. We will assume 1 pint of paint covers 400 square feet. How much paint does Peter need to buy?

The roof of the cottage does not include the base of the pyramid. Therefore, we only need to find the area of the 4 triangular faces. This is called the lateral area. So the lateral area is equal to the surface area minus the area of the base. So all we need is:

\(LA=\frac{1}{2}ps\)

The perimeter of our square is equal to 4 times the side length.

\(LA=\frac{1}{2}(4\times 22)(14)\)

Which we can plug into a calculator to get:

\(LA=616 \text{ ft}^{2}\)

So we will need 616 square feet to be covered.

If 1 pint of paint covers 400 square feet, we need to divide 616 by 400 to figure out how much paint we need. So:

\(616\div 400=1.54\)

So, Peter will need to buy 2 pints of paint to cover the roof of the cottage because 1 pint won’t be enough and you can’t get 0.54 of a pint. So 2 pints of paint will cover the whole roof.

I hope this video on finding the volume and surface area of a pyramid was helpful! Thanks for watching, and happy studying!