Formula | How To Calculate Percentage? - Cuemath

Percentage

The term "percentage" was adapted from the Latin word "per centum", which means "by the hundred". Percentages are fractions with 100 as the denominator. In other words, it is the relation between part and whole where the value of "whole" is always taken as 100.

For example, if the marks of a student in math are 15 out of 50 then the corresponding percentage can be calculated by expressing "marks obtained" as a fraction of "total marks" and multiplying the result by 100. i.e., percentage of marks = 15 / 50 × 100 = 30%. Learn more about percentages and how to convert them into fractions and decimals.

1.	What is Percentage?
2.	Calculating Percentage
3.	Percentage Formula
4.	Conversion Between Percentages and Decimals
5.	Percentage Change Between Two Numbers
6.	FAQs on Percentage

What is the Percentage?

The percentage is a fraction or a ratio in which the value of the whole (denominator) is always 100. For example, if Sam scored 30% marks in his math test, it means that he scored 30 marks out of 100. It is written as 30/100 in the fraction form and 30:100 in terms of ratio. Here "%" is the symbol of percentage and is read as "percent" or "percentage". This percent symbol can always be replaced with "divided by 100" to convert it into a fraction or decimal equivalent.

Examples of Percentage

• 10% = 10/100 ( = 1/10 (or) 0.1)
• 25% = 25/100 ( = 1/4 (or) 0.25)
• 12.5% = 12.5/100 ( = 1/8 (or) 0.125)
• 50% = 50/100 ( = 1/2 (or) 0.5)

Calculating Percentage

Calculating percentage means finding the share out of the whole, in terms of 100. There are two ways to calculate percentage:

• By changing the denominator of the fraction to 100: In this method, we just find the equivalent fraction of a given fraction such that the resultant denominator is 100. Then the numerator itself is the percentage. For example: 4/25 = 4/25 × 4/4 = 16/100 = 16%
• By using the unitary method: In this method, we just multiply the fraction by 100 to get the percentage. For example, the percentage that corresponds to the fraction 4/25 is: 4/25 × 100 = 400/25 = 16%

It should be noted that the first method for calculating the percentage is not suggested in situations where the denominator is not a factor of 100. In such cases, we use the unitary method. Let's see how to find the percentage using the two methods given above in detail.

Finding Percentage When the Total is 100

When we have two or more values that add up to 100, the percentage of those individual values to the total value is that number itself. For example, Sally bought tiles of three different colors for her house. The details of the purchase are given in the following table.

Colour	Number of Tiles	Rate per Hundred	Fraction	Percentage	Read as
Yellow	39	39	39/100	39%	39 percent
Green	26	26	26/100	26%	26 percent
Red	35	35	35/100	35%	35 percent

Finding Percentage When the Total is NOT 100

Since the total number of items adds up to 100, the percentages could be easily calculated as shown above. What if the total number of items does not add up to 100? Let us see.

For example, Emma has a bracelet that is made up 8 red beads and 12 blue beads. Here, the total number of beads is 8 + 12 = 20 (which is not equal to 100). In this case, the percentages can be calculated as shown in the table below (using the unitary method).

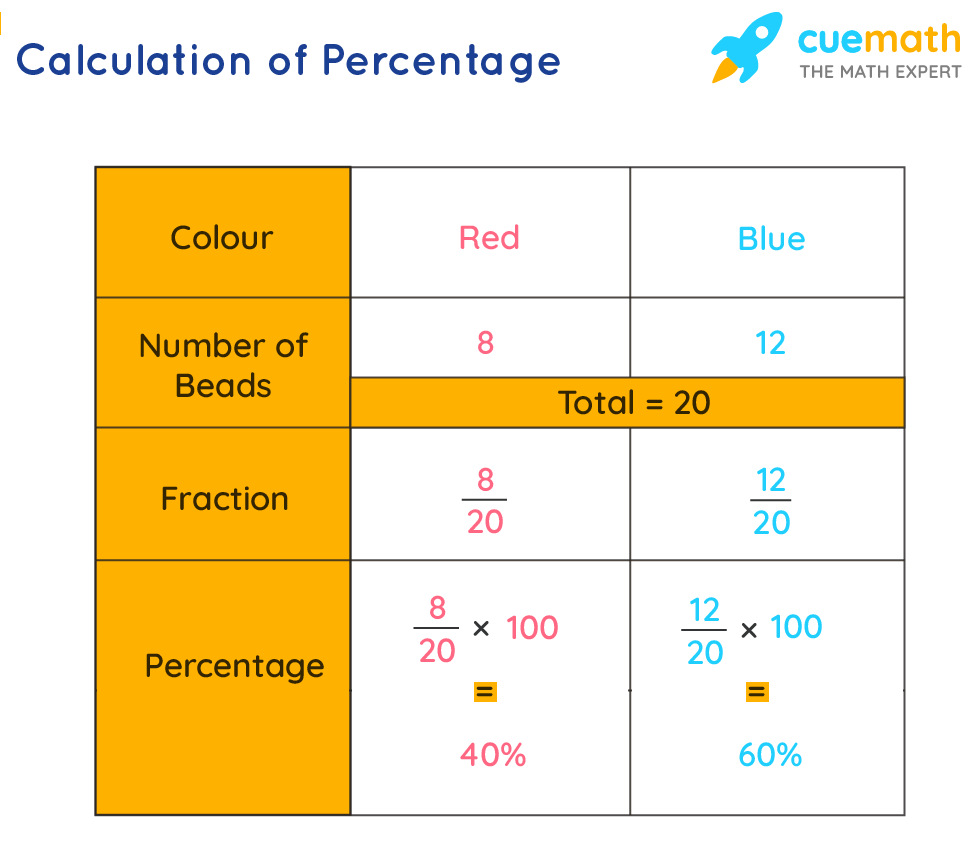
But here, the percentages can be calculated by making the denominators 100 as well. Then we get

• Percentage of red beads = 8/20 × 5/5 = 40/100 = 40%
• Percentage of blue beads = 12/20 × 5/5 = 60/100 = 60%

Look at the following example which shows the advantage of the unitary method over the other method.

Example: How to calculate the percentage of marks of a student who scored 35 out of 40 in math?

Solution: Here, the marks of the student are 35/40. But here, the denominator is not a factor of 100. Thus, finding the percentage in the unitary method is helpful here.

Percentage of marks = 35/40 × 100 = 87.5%.

Percentage Formula

The percentage formula is used to find the share of a whole in terms of 100. Using this formula, you can represent a number as a fraction of 100. If you observe carefully, all three ways to get the percentage shown above can be easily calculated by using the formula given below:

Percentage = (Value/Total Value)×100

Example: In a class of 40 children, 10 are girls. Then what is the percentage of girls?

Solution: Here, the number of girls = 10.

The total number of children = 40.

By the percentage formula,

the percentage of girls = 10/40 × 100 = 25%.

Conversion Between Percentages and Decimals

As we have already seen, the % symbol can always be replaced with "/100". The following points should be taken care of while converting percentages into decimals and vice versa.

• to convert percentages into decimals, just replace % with "divided by 100". For example, 40% = 40/100 = 0.4.
• to convert decimals into percentages, just multiply by 100. For example, 0.4 = 0.4 × 100 = 40%.

Percentage Change Between Two Numbers

Percentage change is the change in the value of a quantity over a period of time in terms of percentage. For example, an increase in population, a decrease in poverty, and so on. We have the formula to show the change in quantity as a percentage. There are two cases that might arise while calculating percentage change and those are:

• Calculate percentage increase
• Calculate percentage decrease

Percentage Increase

Percentage increase refers to the percentage change in the value when it is increased over a period of time. For example, population increase, increase in the number of bacteria on a surface, etc. Percentage increase can be calculated by using the following formula:

Percentage Increase = (Increased Value-Original value)/Original value × 100

Example: The cost of a jacket is increased from $100 to $150. Then by what percentage the price is increased?

Solution: Percentage increase = (150 - 100) / 100 × 100 = 50%.

Percentage Decrease

Percentage decrease refers to the percentage change in the value when it is decreased over a period of time. For example, decrease in the level of rainfall, decrease in the number of Covid patients, etc. Percentage decrease can be calculated by using the following formula:

Percentage Decrease= (Original value-Decreased Value)/Original Value × 100

Example: The amount of rainfall has decreased from 127 mm to 103 mm. Then what is the corresponding percentage decrease?

Solution: Percentage decrease = (127 - 103) / 127 × 100 = 18.9% (Approximately).

Important Points on Percentages:

• To calculate the percentage of a number out of the total number, just use the formula number / total number × 100.
• An increase or decrease in any quantity can be expressed as a percentage. This is referred to as percentage change.
• Fractions can be converted into percentages and vice-versa. To convert the fractions into percentages, multiply by 100. To convert percentages into fractions, divide by 100.
• Percentages are reversible. For example, 50% of 60 is the same as 60% of 50.

☛ Related Topics:

• Percentage Calculator
• Percent to Decimal Calculator
• Decimal to Percent Calculator
• Percent to Fraction Calculator

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.