Hexagon Calculator | 6 - Sided Polygon
Maybe your like
- How many sides does a hexagon have? Exploring the 6-sided shape
- Hexagon definition, what is a regular hexagon?
- Hexagon area formula: how to find the area of a hexagon
- Diagonals of a hexagon
- Circumradius and inradius
- How to draw a hexagon shape
- The easiest way to find a hexagon side, area...
- Hexagon tiles and real-world uses of the 6-sided polygon
- Honeycomb pattern – why the 6-sided shape is so prevalent in nature
- FAQs
Welcome to the hexagon calculator, a handy tool when dealing with any regular hexagon. The hexagon shape is one of the most popular shapes in nature, from honeycomb patterns to hexagon tiles for mirrors – its uses are almost endless. Here we explain not only why the 6-sided polygon is so popular but also how to draw hexagon sides correctly. We also answer the question "what is a hexagon?" using the hexagon definition.
With our hexagon calculator, you can explore many geometrical properties and calculations, including how to find the area of a hexagon, as well as teach you how to use the calculator to simplify any analysis involving this 6-sided shape.
How many sides does a hexagon have? Exploring the 6-sided shape
It should be no surprise that the hexagon (also known as the "6-sided polygon") has precisely six sides. This fact is true for all hexagons since it is their defining feature. The length of the sides can vary even within the same hexagon, except when it comes to the regular hexagon, in which all sides must have equal length.
We will dive a bit deeper into such shape later on when we deal with how to find the area of a hexagon. For now, it suffices to say that the regular hexagon is the most common among 6-sided polygons and the one most often found in nature.
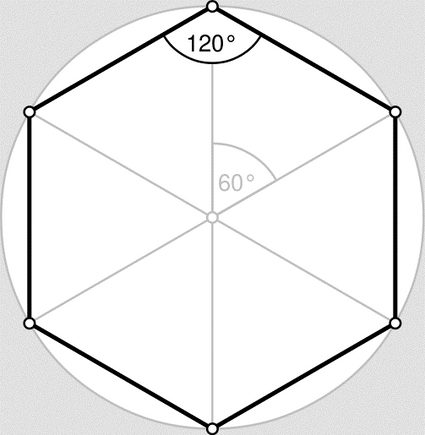
There will be a whole section dedicated to the important properties of the regular hexagon shape, but first, we need to know the technical answer to: "What is a hexagon?" Answering this question will help us understand the tricks we can use to calculate the area of a hexagon without using the hexagon area formula blindly. These tricks involve using other polygons such as squares, triangles and even parallelograms.
Hexagon definition, what is a regular hexagon?
As we've already mentioned, the regular hexagon must have all sides of equal length and all its internal angles must be equal. Each side length is equally valid (as long as it's shared by all 6 sides!), so computing the perimeter of a hexagon is so simple you don't even need the perimeter of a polygon calculator. Just calculate:
- perimeter = 6 × side
The angles of an arbitrary hexagon can have any value, but they all must sum up to 720º (you can easily convert them to other units using our angle conversion calculator). As the regular hexagon requires that all angles are equal, it follows that each individual angle must be 120º. This fact proves to be of the utmost importance when we talk about the popularity of the hexagon shape in nature. It will also be helpful when we explain how to find the area of a regular hexagon. We'll use it also to find the area formula for regular hexagons.
Hexagon area formula: how to find the area of a hexagon
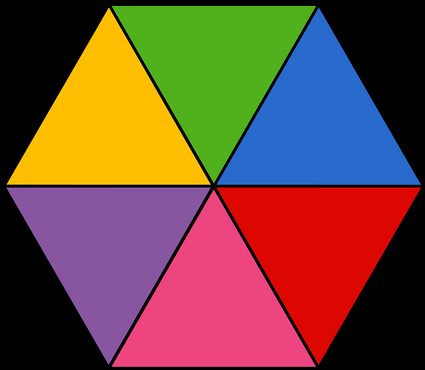
We will now take a look at how to find the area of a hexagon using different tricks. The easiest way is to use our hexagon calculator, which includes a built-in area conversion tool. For those who want to know how to do this by hand, we will explain how to find the area of a regular hexagon with and without the hexagon area formula. The formula for the area of a polygon is always the same no matter how many sides it has as long as it is a regular polygon:
- area = apothem × perimeter / 2
Just as a reminder, the apothem is the distance between the midpoint of any side and the center. You can view it as the height of the equilateral triangle formed by taking one side and two radii of the hexagon (each of the colored areas in the image above). Alternatively, one can also think about the apothem as the distance between the center, and any side of the hexagon since the Euclidean distance is defined using a perpendicular line.
If you don't remember the formula, you can always think about the 6-sided polygon as a collection of 6 triangles. For the regular hexagon, these triangles are equilateral triangles. This fact makes it much easier to calculate their area than if they were isosceles triangles or even 45 45 90 triangles as in the case of a square.
For the regular triangle, all sides are of the same length, which is the length of the side of the hexagon they form. We will call this a. And the height of a triangle will be h = √3/2 × a, which is the exact value of the apothem in this case. We remind you that √ means square root. Using this, we can start with the maths:
- A₀ = a × h / 2
- = a × √3/2 × a / 2
- = √3/4 × a²
Where A₀ means the area of each of the equilateral triangles in which we have divided the hexagon. After multiplying this area by six (because we have 6 triangles), we get the hexagon area formula:
-
A = 6 × A₀ = 6 × √3/4 × a²
-
A = 3 × √3/2 × a²
-
= (√3/2 × a) × (6 × a) /2
-
= apothem × perimeter /2
We hope you can see how we arrive at the same hexagon area formula we mentioned before.
If you want to get exotic, you can play around with other different shapes. For example, suppose you divide the hexagon in half (from vertex to vertex). In that case, you get two trapezoids, and you can calculate the area of the hexagon as the sum of them. You could also combine two adjacent triangles to construct a total of 3 different rhombuses and calculate the area of each separately. You can even decompose the hexagon in one big rectangle (using the short diagonals) and 2 isosceles triangles!
Feel free to play around with different shapes and calculators to see what other tricks you can come up with. Try to use only right triangles or maybe even special right triangles to calculate the area of a hexagon!
Diagonals of a hexagon
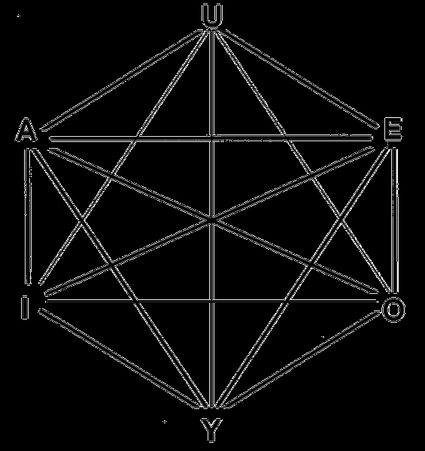
The total number of hexagon diagonals is equal to 9 – three of these are long diagonals that cross the central point, and the other six are the so-called "height" of the hexagon. Our hexagon calculator can also spare you some tedious calculations on the lengths of the hexagon's diagonals. Here is how you calculate the two types of diagonals:
-
Long diagonals – They always cross the central point of the hexagon. As you can notice from the picture above, the length of such a diagonal is equal to two edge lengths:
D = 2 × a
-
Short diagonals – They do not cross the central point. They are constructed by joining two vertices, leaving exactly one in between them. Their length is equal to d = √3 × a.
Circumradius and inradius
Another pair of values that are important in a hexagon are the circumradius and the inradius. The circumradius is the radius of the circumference that contains all the vertices of the regular hexagon. The inradius is the radius of the biggest circle contained entirely within the hexagon.
-
Circumradius: to find the radius of a circle circumscribed on the regular hexagon, you need to determine the distance between the central point of the hexagon (that is also the center of the circle) and any of the vertices. It is simply equal to R = a.
-
Inradius: the radius of a circle inscribed in the regular hexagon is equal to half of its height, which is also the apothem: r = √3/2 × a.
How to draw a hexagon shape
Now we will explore a more practical and less mathematical world: how to draw a hexagon. For a random (irregular) hexagon, the answer is simple: draw any 6-sided shape so that it is a closed polygon, and you're done. But for a regular hexagon, things are not so easy since we have to make sure all the sides are of the same length.

To get the perfect result, you will need a drawing compass. Draw a circle, and, with the same radius, start making marks along it. Starting at a random point and then making the next mark using the previous one as the anchor point, draw a circle with the compass. You will end up with 6 marks, and if you join them with the straight lines, you will have yourself a regular hexagon. You can see a similar process in the animation above.
The easiest way to find a hexagon side, area...
The hexagon calculator allows you to calculate several interesting parameters of the 6-sided shape that we usually call a hexagon. Using this calculator is as simple as it can possibly get with only one of the parameters needed to calculate all others and includes a built-in length conversion tool for each of them.
We have discussed all the parameters of the calculator, but for the sake of clarity and completeness, we will now go over them briefly:
- Area – 2–D surface enclosed by the hexagon shape;
- Side Length – Distance from one vertex to the next consecutive one;
- Perimeter – Sum of the lengths of all hexagon sides;
- Long Diagonal – Distance from one vertex to the opposite one;
- Short Diagonal – Distance between two vertices that have another vertex between them;
- Circumcircle radius – Distance from the center to a vertex (Same as the radius of the hexagon); and
- Incircle radius – Same as the apothem.
Hexagon tiles and real-world uses of the 6-sided polygon
Everyone loves a good real-world application, and hexagons are definitely one of the most used polygons in the world. Starting with human usages, the easiest (and probably least exciting) use is hexagon tiles for flooring purposes. The hexagon is an excellent shape because it perfectly fits with one another to cover any desired area. If you're interested in such a use, we recommend the flooring calculator and the square footage calculator as they are excellent tools for this purpose.
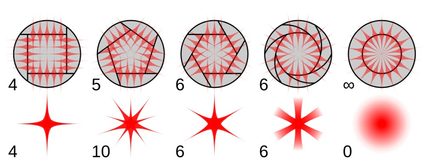
The next case is common to all polygons, but it is still interesting to see. In photography, the opening of the sensor almost always has a polygonal shape. This part of the camera is called the aperture and dictates many properties and features of the pictures produced by a camera. The most unexpected one is the shape of very bright (point-like) objects due to the effect called diffraction grating, and it is illustrated in the picture above.

One of the most valuable uses of hexagons in the modern era, closely related to the one we've talked about in photography, is in astronomy. One of the biggest problems we experience when observing distant stars is how faint they are in the night sky. That is because despite being very bright objects, they are so very far away that only a tiny fraction of their light reaches us; you can learn more about that in our luminosity calculator. On top of that, due to relativistic effects (similar to time dilation and length contraction), their light arrives on the Earth with less energy than it was emitted. This effect is called the red shift.

The result is that we get a tiny amount of energy with a longer wavelength than we would like. The best way to counteract this is to build telescopes as enormous as possible. The problem is that making a one-piece lens or mirror larger than a couple of meters is almost impossible, not to talk about the issues with logistics. The solution is to build a modular mirror using hexagonal tiles like the ones you can see in the pictures above.
Making such a big mirror improves the angular resolution of the telescope, as well as the magnification factor due to the geometrical properties of a "Cassegrain telescope". So we can say that thanks to regular hexagons, we can see better, further, and more clearly than we could have ever done with only one-piece lenses or mirrors.
Did you know that hexagon quilts are also a thing?? Discover more with Omni's hexagon quilt calculator!
Honeycomb pattern – why the 6-sided shape is so prevalent in nature
The honeycomb pattern is composed of regular hexagons arranged side by side. They completely fill the entire surface they span, so there aren't any holes in between them. This honeycomb pattern appears not only in honeycombs (surprise!) but also in many other places in nature. In fact, it is so popular that one could say it is the default shape when conflicting forces are at play and spheres are not possible due to the nature of the problem.
From bee 'hives' to rock cracks through organic chemistry (even in the build blocks of life: proteins), regular hexagons are the most common polygonal shape that exists in nature. And there is a reason for that: the hexagon angles. The 120º angle is the most mechanically stable of all, and coincidentally it is also the angle at which the sides meet at the vertices when we line up hexagons side by side. For a full description of the importance and advantages of regular hexagons, we recommend watching this video.
The way that 120º angles distribute forces (and, in turn, stress) amongst 2 of the hexagon sides makes it a very stable and mechanically efficient geometry. This is a significant advantage that hexagons have. Another important property of regular hexagons is that they can fill a surface with no gaps between them (along with regular triangles and squares). On top of that, the regular 6-sided shape has the smallest perimeter for the biggest area among these surface-filling polygons, which makes it very efficient.

A fascinating example in this video is that of the soap bubbles. When you create a bubble using water, soap, and some of your own breath, it always has a spherical shape. This result is because the volume of a sphere is the largest of any other object for a given surface area.
However, when we lay the bubbles together on a flat surface, the sphere loses its efficiency advantage since the section of a sphere cannot completely cover a 2D space. The next best shape in terms of volume-to-surface area ratio also happens to be the best at balancing the inter-bubble tension that is created on the surface of the bubbles. We are, of course, talking of our almighty hexagon.
Bubbles present an interesting way of visualizing the benefits of a hexagon over other shapes, but it's not the only way. In nature, as we have mentioned, there are plenty of examples of hexagonal formations, mostly due to stress and tensions in the material. We cannot go over all of them in detail, unfortunately. We can, however, name a few places where one can find regular hexagonal patterns in nature:
- Honeycombs;
- Organic compounds ;
- Stacks of bubbles;
- Rock formations (like Giant's);
- Eyes of insects;
- ...
FAQs
What is the apothem in a hexagon?
In a hexagon, the apothem is the distance between the midpoint of any side and the center of the hexagon. When you imagine a hexagon as six equilateral triangles that all share a vertex at the hexagon's center, the apothem is the height of each of these triangles.
How do I find the area of a hexagon given perimeter?
To determine the area of a hexagon with perimeter P:
-
Divide P by 6 to get the side length a.
-
Find the square of the side length: a².
-
Multiply a² by 3√3 / 2.
-
The result is the area of your hexagon!
-
You could also go directly from P to the area by using the formula area = √3 P² / 24.
What is the apothem of a hexagon with side 2?
The answer is √3, that is, approximately 1.73. This is because of the relationship apothem = ½ × √3 × side. When we plug in side = 2, we obtain apothem = √3, as claimed.
What is the area of a hexagon with side 1?
The answer is 3√3/2, that is, approximately, 2.598. To arrive at this result, you can use the formula that links the area and side of a regular hexagon. It reads area = 3√3/2 × side², so we immediately obtain the answer by plugging in side = 1.

A labelled hexagon.
© Omni Calculator
Side (a)
Area
Perimeter
Long diagonal (d)
Short diagonal (s)
Circumcircle radius (R)
Apothem (r)
Share result
Reload calculatorClear all changesDid we solve your problem today?
Yes
No
Check out 26 similar 2d geometry calculators 📏
Area
Area of a rectangle
Area of crescent
Tag » How To Find Perimeter Of Hexagon
-
High School Math : How To Find The Perimeter Of A Hexagon
-
Intermediate Geometry : How To Find The Perimeter Of A Hexagon
-
Perimeter Of Hexagon | Formula, Examples & Application
-
What Is Hexagon Formula? Examples - Cuemath
-
Perimeter Of Hexagon, Perimeter For Regular And ... - YouTube
-
The Perimeter Of Hexagon Formula - Vedantu
-
Perimeter Of Hexagon Formula - Byju's
-
Perimeter Of A Hexagon - Formulas And Examples - Mechamath
-
Perimeter And Area Of Regular Hexagon | Solved Example Problems
-
Perimeter Of Hexagon Formula: Definition, Derivation And Examples
-
What Is The Perimeter Of A Hexagon? - Quora
-
Perimeter Of Hexagon Formula - GeeksforGeeks
-
Write A Program To Calculate The Perimeter Of Hexagon - Javatpoint