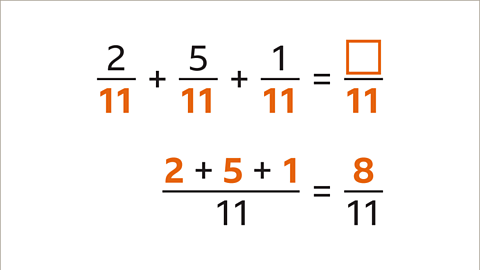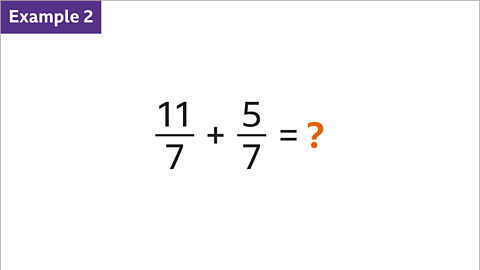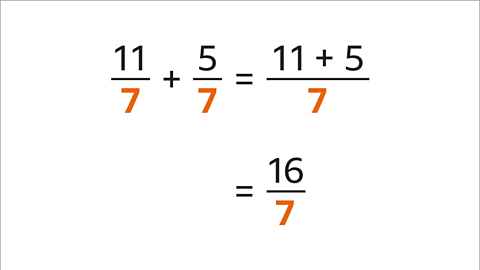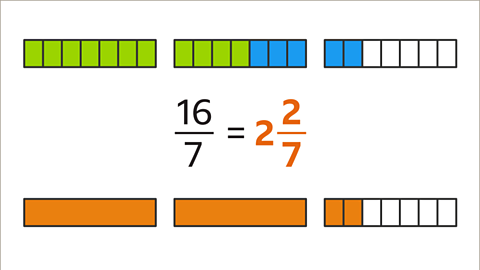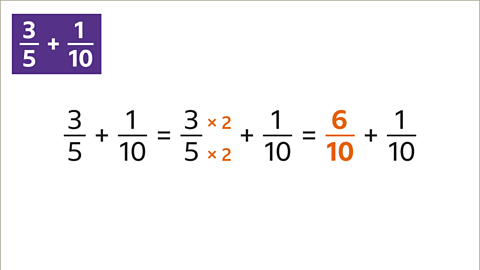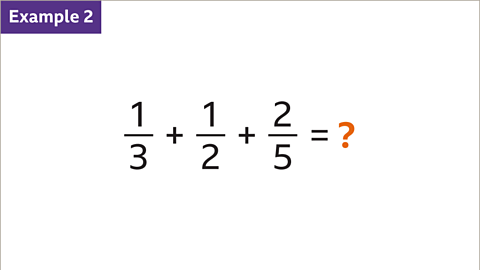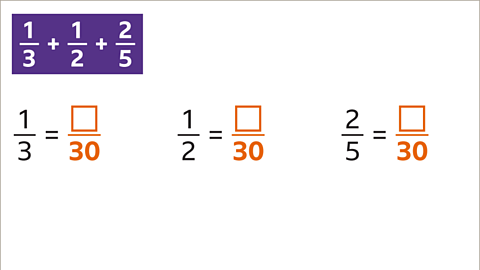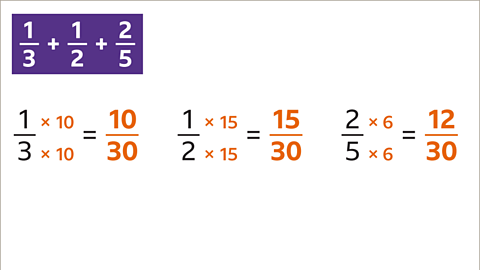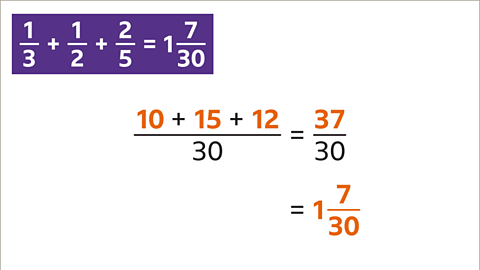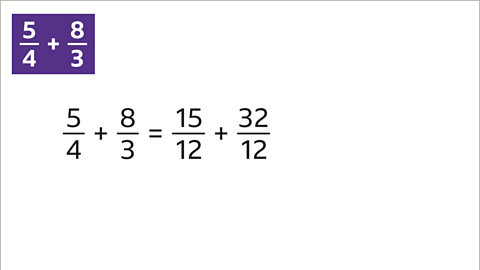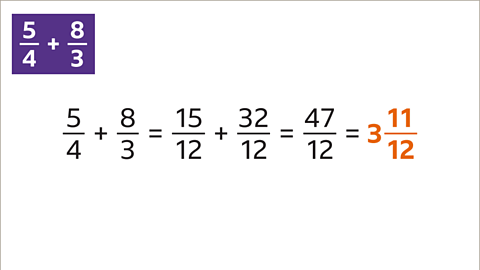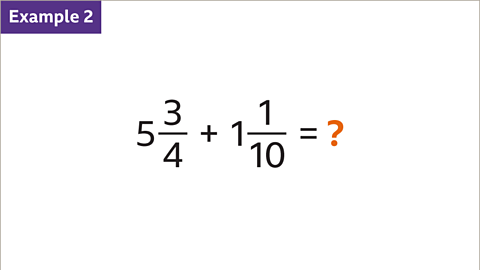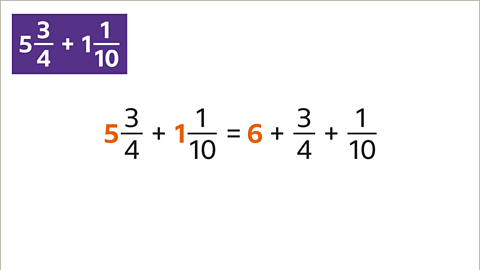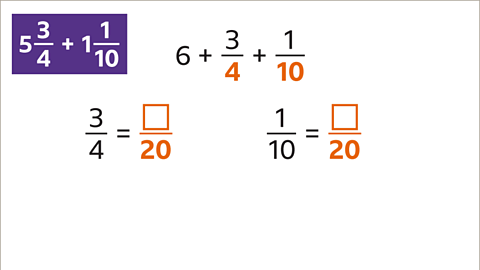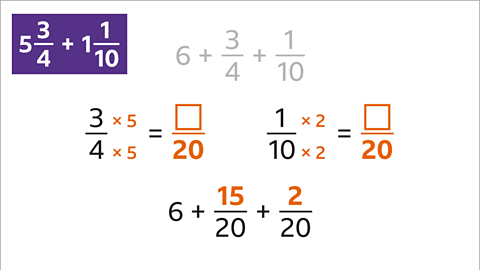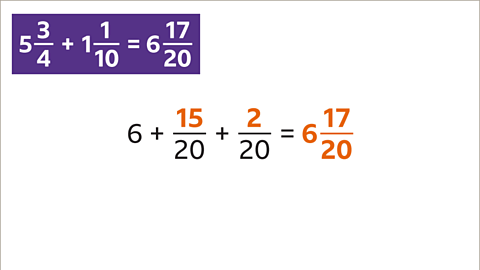How To Add Fractions - KS3 Maths – BBC Bitesize

Home » How To Add Improper Fractions » How To Add Fractions - KS3 Maths – BBC Bitesize

Maybe your like

  1. Key points
  2. Add fractions with the same denominators
    1. Examples
    2. Question
  3. Adding with different denominators
    1. Examples
    2. Question
  4. Adding improper fractions mixed numbers
    1. Examples
    2. Question
    3. Question
  5. Practise adding fractions
  6. Real-world maths

Key points

Fractions can be added in different ways:

  • When fractions have the same denominator, the numerators are added to give the total.
  • When fractions have different denominators, equivalent fractions are used that have the same denominator. The denominator of the equivalent fractions will be the lowest common multiple, which is found by listing the multiples of each number and circling any common multiples to find the lowest.
  • Improper fractions can be added as fractions or they can be converted to mixed numbers and then added.
  • To add mixed numbers, add the integer parts and fractions separately.
  • Learning about equivalent fractions and converting between improper fractions and mixed numbers is useful when adding fractions.
Back to top

Adding fractions with the same denominators

  1. When the denominators are the same, add the numerators.

  2. Sometimes the final answer can be simplified.

  3. If the final answer is an improper fraction, the answer can be left as an improper fraction or it could be written as a mixed number.

Examples

Image gallerySkip image gallery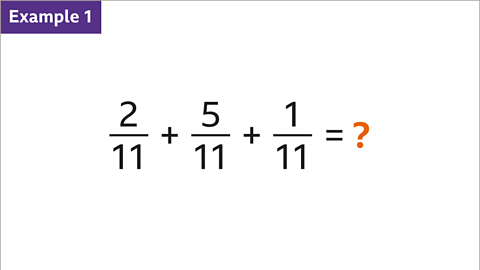
  1. Example 1: Two elevenths plus five elevenths plus one eleventh equals question mark (highlighted).
    Image caption,

    Add these fractions with the same denominators.

1 of 6

Previous imageNext imageSlide 1 of 6, Example 1: Two elevenths plus five elevenths plus one eleventh equals question mark (highlighted)., Add these fractions with the same denominators.End of image gallery

Question

Add the fractions.

\( \frac{8}{15} + \frac{11}{15} = \) ?

Show answer

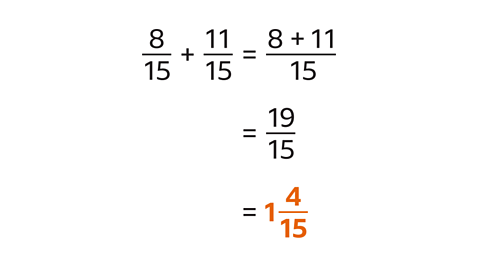
Eight fifteenths plus eleven fifteenths equals eight plus eleven over fifteen. Equals nineteen fifteenths. Equals one and four fifteenths – highlighted.
  • The denominators are the same - the answer will be in fifteenths.
  • Add the numerators. 8 + 11 = 19
  • The sum is \( \frac{19}{15} \). This is \( 1 \frac{4}{15} \) as a mixed number.
Back to top

Adding fractions with different denominators

  1. Find the lowest common multiple (LCM) of the denominators.

  2. Rewrite the fractions as equivalent fractions with the same denominator.

  3. Add the numerators.

  4. Simplify where possible.

  5. If the sum is an improper fraction, the answer can be left as an improper fraction or it can be written as a mixed number.

Any common multiple of the denominators can be used as the common denominator. However, the most efficient way of adding fractions with different denominators is to use the LCM.

Examples

Image gallerySkip image gallery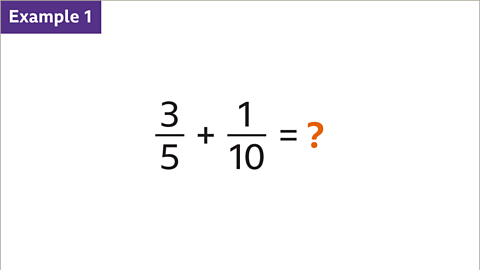
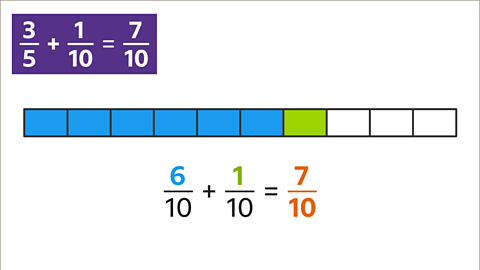
  1. Example 1: Three fifths plus one tenth equals question mark (highlighted).
    Image caption,

    What is 3⁄5 + 1⁄10?

1 of 7

Previous imageNext imageSlide 1 of 7, Example 1: Three fifths plus one tenth equals question mark (highlighted)., What is 3⁄5 + 1⁄10?End of image gallery

Question

Add the fractions \( \frac{2}{5} + \frac{3}{8} = \) ?

Show answer

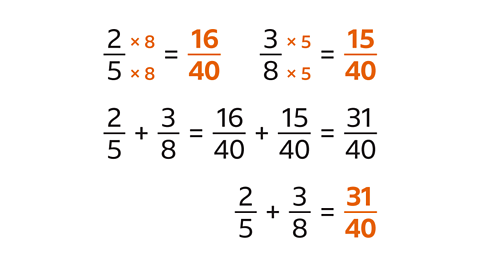
Two fifths multiplied by eight equals sixteen fortieths (highlighted). Three eighths multiplied by five equals fifteen fortieths (highlighted). Two fifths plus three eighths equals sixteen fortieths plus fifteen fortieths equals thirty-one fortieths. Two fifths plus three eighths equals thirty-one fortieths (highlighted).

  1. Find the LCM. The LCM of 5 and 8 is 40

  2. Create equivalent fractions with a denominator of 40. \( \frac{2}{5} \) is equivalent to \( \frac{16}{40} \) and \( \frac{3}{8} \) is equivalent to \( \frac{15}{40} \)

  3. Add the numerators. 16 + 15 = 31

The fractions add up to \( \frac{31}{40} \)

\( \frac{2}{5} + \frac{3}{8} = \frac{31}{40} \)

Back to top

How to add improper fractions and mixed numbers

To add improper fractions:

  1. The simplest approach is to add the improper fractions using a common denominator.

  2. Alternatively, convert the improper fractions into mixed numbers by dividing the numerator by the denominator. The whole is the integer for the mixed number and the remainder is the numerator for the fraction.

  3. The improper fractions are now mixed numbers. To add these, follow the steps below for adding mixed numbers.

To add mixed numbers:

  1. Add the integers.

  2. Use the LCM of the denominators to rewrite the fractions as equivalent fractions with the same denominator

  3. Add the fractions.

  4. Simplify the answer if possible.

  5. Alternatively change the mixed numbers to improper fractions first and add the improper fractions using a common denominator.

Examples

Image gallerySkip image gallery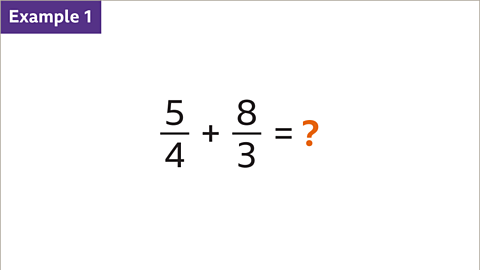
  1. Example 1: Five quarters plus eight thirds equals question mark (highlighted).
    Image caption,

    Add 5⁄4 and 8⁄3

1 of 8

Previous imageNext imageSlide 1 of 8, Example 1: Five quarters plus eight thirds equals question mark (highlighted)., Add 5⁄4 and 8⁄3End of image gallery

Question

Add the mixed numbers. \( 4 \frac{2}{9} + 1 \frac{5}{12} + 2 \frac{1}{18} = \) ?

Show answer

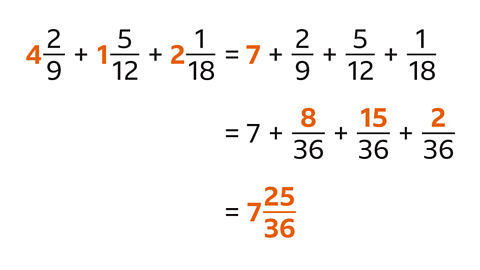
Four and two ninths plus one and five twelfths plus two and one eighteenths equals seven plus two ninths plus five twelfths plus one eighteenths – all whole number highlighted. Equals seven plus eight thirty-sixths plus fifteen thirty-sixths plus two thirty-sixths – all numerators highlighted. Equals seven and twenty-five thirty-sixths – highlighted.
  • Add the integers.
  • The fractions have different denominators.
  • The LCM of 9, 12 and 18 is 36. Rewrite the fractional parts with a denominator of 36. \( \frac{2}{9} \) is equivalent to \( \frac{8}{36} \), \( \frac{5}{12} \) is equivalent to \( \frac{15}{36} \) and \( \frac{1}{18} \) is equivalent to \( \frac{2}{36} \)
  • Add the fractions.

\( 4 \frac{2}{9} + 1 \frac{5}{12} + 2 \frac{1}{18} = 7 \frac{25}{36} \)

Question

Add the mixed numbers \( 2 \frac{3}{4} + 1 \frac{7}{8} = \) ?

  • If the sum of two fractions gives an answer over 1 (an improper fraction), the calculation is completed by changing the improper fraction to a mixed number and adding the integers.

Show answer

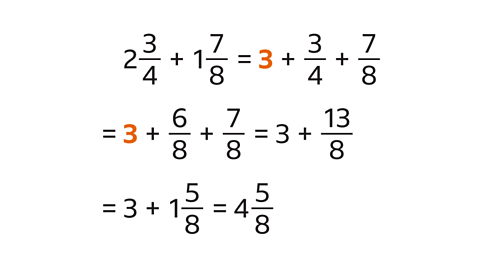
Two and three quarters plus one and seven eighths equals three (highlighted) plus three quarters plus seven eighths. Equals three (highlighted) plus six eighths plus seven eighths equals three plus thirteen eighths. Equals three plus one and five eighths equals four and five eighths.
  • Add the integers.
  • Write the fractions with the same common denominator.
  • Add the fractions.
  • The answer is \( 3 + \frac{13}{8} = 3 + 1 \frac{5}{8} \)
  • The fractions add to over 1. Complete the calculation by adding \( 3 + 1 \frac{5}{8} \) to give \( 4 \frac{5}{8} \)
Back to top

Practise adding fractions

Try this quiz to practise adding fractions. You may need a pen and paper to solve some of these problems.

Back to top

Real-world maths

A woman hanging frames in a baby's nursery.
Image caption, You may need to add fractions when choosing picture frames.

Adding fractions can be used to combine measurements. This can be useful if, for example, you want to add a border to a photograph.

A wide or narrow border can affect the look of a photo. These measurements may involve mixed numbers.

For a picture measuring 24 \( \frac{1}{2} \) cm by 24 \( \frac{1}{2} \) cm with a border of 18 \( \frac{3}{8} \) cm on each side, the total dimensions will be 18 \( \frac{3}{8} \) + 24 \( \frac{1}{2} \) +18 \( \frac{3}{8} \) which is 61 \( \frac{1}{4} \) cm by 61 \( \frac{1}{4} \) cm.

A woman hanging frames in a baby's nursery.
Image caption, You may need to add fractions when choosing picture frames.
Back to top

Play Sudoku with BBC Bitesize!

Every weekday we release brand new easy, medium and hard Sudoku puzzles. Perfect for testing your skill with numbers and logic.

Play Sudoku with BBC Bitesize!Back to top

More on Fractions

Find out more by working through a topic

  • How to subtract fractions

    • count7 of 14

  • How to multiply fractions

    • count8 of 14

  • How to divide fractions

    • count9 of 14

  • How to find a fraction of an amount

    • count10 of 14

Tag » How To Add Improper Fractions