How To Find Orthocenter Of A Triangle With Given Vertices

HOW TO FIND ORTHOCENTER OF A TRIANGLE WITH GIVEN VERTICES

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Orthocenter :

It can be shown that the altitudes of a triangle are concurrent and the point of concurrence is called the orthocenter of the triangle. The orthocenter is denoted by O.

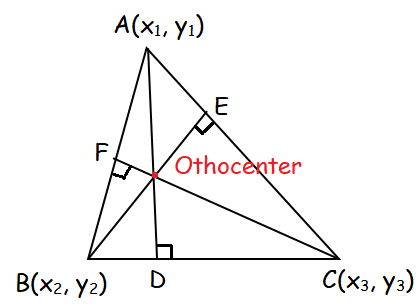
Let ABC be the triangle AD,BE and CF are three altitudes from A, B and C to BC, CA and AB respectively.

Steps Involved in Finding Orthocenter of a Triangle :

• Find the equations of two line segments forming sides of the triangle.
• Find the slopes of the altitudes for those two sides.
• Use the slopes and the opposite vertices to find the equations of the two altitudes.
• Solve the corresponding x and y values, giving you the coordinates of the orthocenter.

Solved Examples

Example 1 :

Find the coordinates of the orthocentre of the triangle whose vertices are (3, 1), (0, 4) and (-3, 1)

Solution :

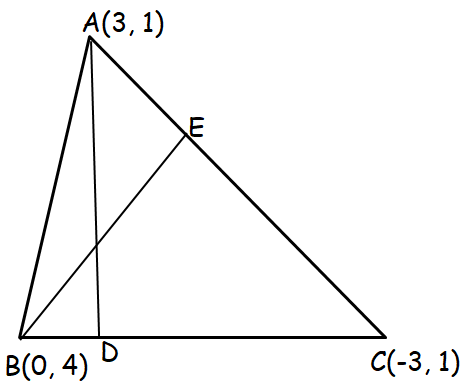
Now we need to find the slope of AC. From that we have to find the slope of the perpendicular line through B.

Slope of AC  =  (y2 - y1) / (x2 - x1)

A (3, 1) and C (-3, 1)

here x1  =  3, y1  =  1, x2  =  -3 and y2  =  1

  =  (1 - 1) / (-3 - 3)

  =  0

Slope of the altitude BE  =  -1/ slope of AC

  =  1/0

Equation of the altitude BE :

  (y - y1)  =  m (x -x1)

Here B (0, 4)  m  =  1/0

(y - 4)  =  (1/0) (x - 0)

(y - 4)  =  x / 0

x  =  0

Now we need to find the slope of BC. From that we have to find the slope of the perpendicular line through D.

Slope of BC  =  (y2 - y1) / (x2 - x1)

B (0, 4) and C (-3, 1)

here x1  =  0, y1  =  4, x2  =  -3 and y2  =  1

  =  [(1 - 4) / (-3 - 0)]

  =  -3 / (-3)

  =  1

Slope of the altitude AD  =  -1/ slope of AC

  =  -1/1

  =  -1

Equation of the altitude AD :

  (y - y1)  =  m (x -x1)

Here A(3, 1)  m = -1

(y - 1)  =  -1(x - 3)

y - 1  =  -x + 3

x + y  =  3 + 1

x + y  =  4 --------(1)

Substitute the value of x in the first equation

0 + y = 4

y = 4

So the orthocentre is (0, 4).

Example 2 :

Find the co ordinates of the orthocentre of a triangle whose vertices are (2, -3) (8, -2) and (8, 6).

Solution :

Let the given points be A (2, -3) B (8, -2) and C (8, 6)

Now we need to find the slope of AC.From that we have to find the slope of the perpendicular line through B.

Slope of AC  =  (y2 - y1) / (x2 - x1)

A (2, -3) and C (8, 6)

here x1  =  2, y1  =  -3, x2  =  8 and y2  =  6

  =  (6 - (-3)) / (8 - 2)

  =  9/6

  = 3/2

Slope of the altitude BE  =  -1/ slope of AC

  =  -1 / (3/2)

  =  -2/3

Equation of the altitude BE :

(y - y1)  =  m (x - x1)

Here B (8, -2) m  =  2/3

y - (-2)  =  (-2/3) (x - 8)

3(y + 2)  =  -2 (x - 8)

3y + 6  =  -2x + 16 

2x + 3y - 16 + 6  =  0

2x + 3y - 10  =  0

Now we need to find the slope of BC. From that we have to find the slope of the perpendicular line through D.

Slope of BC  =  (y2 - y1) / (x2 - x1)

B (8, -2) and C (8, 6)

here x1  =  8, y1  =  -2, x2  =  8 and y2  =  6

  =  (6 - (-2)) / (8 - 8)

  =  8/0  =  undefined

Slope of the altitude AD  =  -1/ slope of AC

  =  -1/undefined

  =  0

Equation of the altitude AD:

(y - y1)  =  m (x - x1)

Here A(2, -3)  m  =  0

y - (-3)  =  0 (x - 2)

y + 3  =  0

y  =  -3

Substitute the value of x in the first equation

2x + 3(-3)  =  10

2x - 9  =  10

2x  =  10 + 9

 2x  =  19

x  =  19/2

So, the orthocentre is (19/2,-3).

Subscribe to our ▶️ YouTube channel 🔴 for the latest videos, updates, and tips.

Kindly mail your feedback to [email protected]

We always appreciate your feedback.

About Us  |  Contact Us  |  Privacy Policy

©All rights reserved. onlinemath4all.com