How To Identify Even And Odd Functions And Their Graphs - Dummies

Marvel fans assemble for the ultimate holiday giveaway! Enter now for your chance to win. Dummies AI Browse Book & Article Categories

Book & Article Categories

closeTechnologyAcademics & The ArtsHome, Auto, & HobbiesBody, Mind, & SpiritBusiness, Careers, & MoneyCollections

Collections

Explore all collectionscloseBYOB (Be Your Own Boss)Be a Rad DadCareer ShiftingContemplating the CosmosFor Those Seeking Peace of MindFor the Aspiring AficionadoFor the Budding Cannabis EnthusiastFor the College BoundFor the Exam-Season CrammerFor the Game Day PrepperCustom Solutions

• Book & Article Categories
• Collections
• Custom Solutions
• Dummies AI

• Main Menu

• Book & Article Categories

• Technology
• Academics & The Arts
• Home, Auto, & Hobbies
• Body, Mind, & Spirit
• Business, Careers, & Money
• Dummies AI

• Main Menu

• Book & Article Categories

• Technology
• Academics & The Arts
• Home, Auto, & Hobbies
• Body, Mind, & Spirit
• Business, Careers, & Money
• Dummies AI

• Main Menu

• Collections

  Explore all collections

• BYOB (Be Your Own Boss)
• Be a Rad Dad
• Career Shifting
• Contemplating the Cosmos
• For Those Seeking Peace of Mind
• For the Aspiring Aficionado
• For the Budding Cannabis Enthusiast
• For the College Bound
• For the Exam-Season Crammer
• For the Game Day Prepper
• Dummies AI

HomeAcademics & The Arts ArticlesMath ArticlesPre-Calculus ArticlesHow to Identify Even and Odd Functions and their GraphsByMary Jane Sterling Updated2021-12-21 20:39:55From the bookPre-Calculus Workbook For DummiesShare

• 
• 
• 
• 
• 

Download E-BookPre-Calculus Workbook For Dummies Explore Book Pre-Calculus All-in-One For Dummies Explore BookBuy NowBuy on AmazonBuy on WileySubscribe on PerlegoDownload E-BookPre-Calculus Workbook For DummiesExplore Book Pre-Calculus All-in-One For DummiesExplore BookBuy NowBuy on AmazonBuy on WileySubscribe on PerlegoKnowing whether a function is even or odd helps you to graph it because that information tells you which half of the points you have to graph. These types of functions are symmetrical, so whatever is on one side is exactly the same as the other side.

If a function is even, the graph is symmetrical about the y-axis. If the function is odd, the graph is symmetrical about the origin.

• Even function: The mathematical definition of an even function is f(–x) = f(x) for any value of x. The simplest example of this is f(x) = x2 because f(x)=f(-x) for all x. For example, f(3) = 9, and f(–3) = 9. Basically, the opposite input yields the same output.

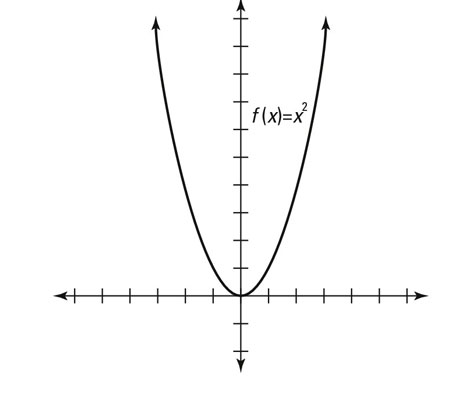  Visually speaking, the graph is a mirror image about the y-axis, as shown here.

• Odd function: The definition of an odd function is f(–x) = –f(x) for any value of x. The opposite input gives the opposite output. These graphs have 180-degree symmetry about the origin. If you turn the graph upside down, it looks the same.

  

  The example shown above, f(x) = x3, is an odd function because f(-x)=-f(x) for all x. For example, f(3) = 27 and f(–3) = –27.

About This Article

This article is from the book: 

Pre-Calculus Workbook For Dummies

About the book author:

Mary Jane Sterling (Peoria, Illinois) is the author of Algebra I For Dummies, Algebra Workbook For Dummies, Algebra II For Dummies, Algebra II Workbook For Dummies, and many other For Dummies books. She taught at Bradley University in Peoria, Illinois for more than 30 years, teaching algebra, business calculus, geometry, and finite mathematics.

This article can be found in the category: 

Pre-CalculusGet a Subscription