How To Recognize A P-Series

Flag Football For Dummies is here!  Get your game on and order your copy today! Dummies AI Browse Book & Article Categories

Book & Article Categories

closeTechnologyAcademics & The ArtsHome, Auto, & HobbiesBody, Mind, & SpiritBusiness, Careers, & MoneyCollections

Collections

Explore all collectionscloseBYOB (Be Your Own Boss)Be a Rad DadCareer ShiftingContemplating the CosmosFor Those Seeking Peace of MindFor the Aspiring AficionadoFor the Budding Cannabis EnthusiastFor the College BoundFor the Exam-Season CrammerFor the Game Day PrepperCustom Solutions

• Book & Article Categories
• Collections
• Custom Solutions
• Dummies AI

• Main Menu

• Book & Article Categories

• Technology
• Academics & The Arts
• Home, Auto, & Hobbies
• Body, Mind, & Spirit
• Business, Careers, & Money
• Dummies AI

• Main Menu

• Book & Article Categories

• Technology
• Academics & The Arts
• Home, Auto, & Hobbies
• Body, Mind, & Spirit
• Business, Careers, & Money
• Dummies AI

• Main Menu

• Collections

  Explore all collections

• BYOB (Be Your Own Boss)
• Be a Rad Dad
• Career Shifting
• Contemplating the Cosmos
• For Those Seeking Peace of Mind
• For the Aspiring Aficionado
• For the Budding Cannabis Enthusiast
• For the College Bound
• For the Exam-Season Crammer
• For the Game Day Prepper
• Dummies AI

HomeAcademics & The Arts ArticlesMath ArticlesCalculus ArticlesHow to Recognize a P-SeriesByMark Zegarelli Updated2016-03-26 18:31:18From the bookCalculus II For DummiesShare

• 
• 
• 
• 
• 

Download E-BookCalculus II For Dummies Explore Book Calculus II Workbook For Dummies Explore BookBuy NowBuy on AmazonBuy on WileySubscribe on PerlegoDownload E-BookCalculus II For DummiesExplore Book Calculus II Workbook For DummiesExplore BookBuy NowBuy on AmazonBuy on WileySubscribe on Perlego

An important type of series is called the p-series. A p-series can be either divergent or convergent, depending on its value. It takes the following form:

Here’s a common example of a p-series, when p = 2:

Here are a few other examples of p-series:

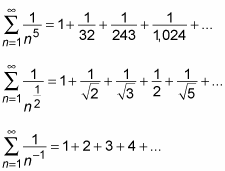
Remember not to confuse p-series with geometric series. Here’s the difference:

• A geometric series has the variable n in the exponent — for example,

  

• A p-series has the variable in the base — for example

  

As with geometric series, a simple rule exists for determining whether a p-series is convergent or divergent.

A p-series converges when p > 1 and diverges when p

Here are a few important examples of p-series that are either convergent or divergent.

When p = 1: the harmonic series

When p = 1, the p-series takes the following form:

This p-series is important enough to have its own name: the harmonic series. The harmonic series is divergent.

When p = 2, p = 3, and p = 4

Here are the p-series when p equals the first few counting numbers greater than 1:

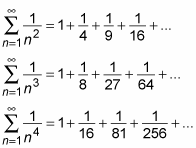
Because p > 1, these series are all convergent.

When p = 1/2

When p = 1/2 the p-series looks like this:

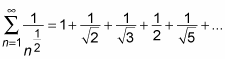
Because p ≤ 1, this series diverges. To see why it diverges, notice that when n is a square number, say n = k2, the nth term equals

So this p-series includes every term in the harmonic series plus many more terms. Because the harmonic series is divergent, this series is also divergent.

About This Article

This article is from the book: 

Calculus II For Dummies

About the book author:

Mark Zegarelli is a math tutor and author of several books, including Basic Math & Pre-Algebra For Dummies.

This article can be found in the category: 

CalculusGet a Subscription