How To Test For Symmetry - Basic Mathematics

Test for symmetry

This lesson will teach you how to test for symmetry. You can test the graph of a relation for symmetry with respect to the x-axis, y-axis, and the origin. In this lesson, we will confirm symmetry algebraically.

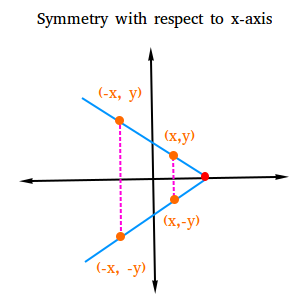
Test for symmetry with respect to the x-axis.

The graph of a relation is symmetric with respect to the x-axis if for every point (x,y) on the graph, the point (x, -y) is also on the graph. To check for symmetry with respect to the x-axis, just replace y with -y and see if you still get the same equation. If you do get the same equation, then the graph is symmetric with respect to the x-axis.

Example #1:is x = 3y4 - 2 symmetric with respect to the x-axis?Replace y with -y in the equation.X = 3(-y)4 - 2X = 3y4 - 2

Since replacing y with -y gives the same equation, the equation x = 3y4 - 2 is symmetric with respect to the x-axis.

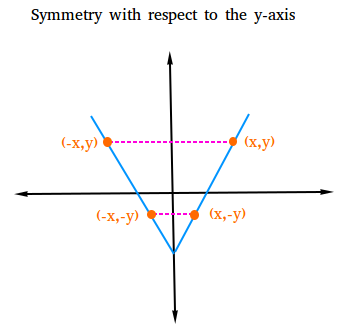
Test for symmetry with respect to the y-axis.

The graph of a relation is symmetric with respect to the y-axis if for every point (x,y) on the graph, the point (-x, y) is also on the graph.To check for symmetry with respect to the y-axis, just replace x with -x and see if you still get the same equation. If you do get the same equation, then the graph is symmetric with respect to the y-axis.

Example #2:is y = 5x2 + 4 symmetric with respect to the x-axis?Replace x with -x in the equation.Y = 5(-x)2 + 4Y = 5x2 + 4

Since replacing x with -x gives the same equation, the equation y = 5x2 + 4 is symmetric with respect to the y-axis.

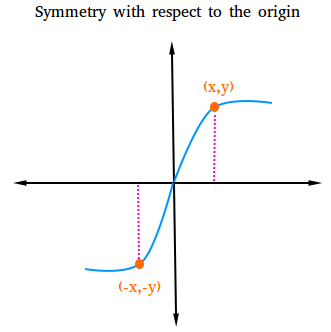
Test for symmetry with respect to the origin.

The graph of a relation is symmetric with respect to the origin if for every point (x,y) on the graph, the point (-x, -y) is also on the graph.To check for symmetry with respect to the origin, just replace x with -x and y with -y and see if you still get the same equation. If you do get the same equation, then the graph is symmetric with respect to the origin.

Example #3:is 2xy = 12 symmetric with respect to the origin?Replace x with -x  and y with -y in the equation.2(-x × -y) = 122xy = 12Since replacing x with -x and y with -y gives the same equation, the equation  2xy = 12  is symmetric with respect to the origin.

Line of symmetry

Email I am at least 16 years of age. I have read and accept the privacy policy. I understand that you will use my information to send me a newsletter. Subscribe FacebookPinterestWhatsApp