Inscribed Angles Of Circles - Krista King Math

About Pricing Login Subscribe Risk Free Inscribed angles of circles

How can we build inscribed angles and their intercepted arcs?

In this lesson we’ll look at inscribed angles of circles and how they’re related to arcs, called intercepted arcs.

Chord of a circle

A chord is a straight line segment that has endpoints on the circumference of the circle. The diameter of a circle is a special type of chord that passes through the circle’s center. The yellow line is an example of a chord.

Inscribed angle

An inscribed angle is formed by two chords. These chords share the vertex of an angle. The arc that touches the endpoints of the chords is called the intercepted arc.

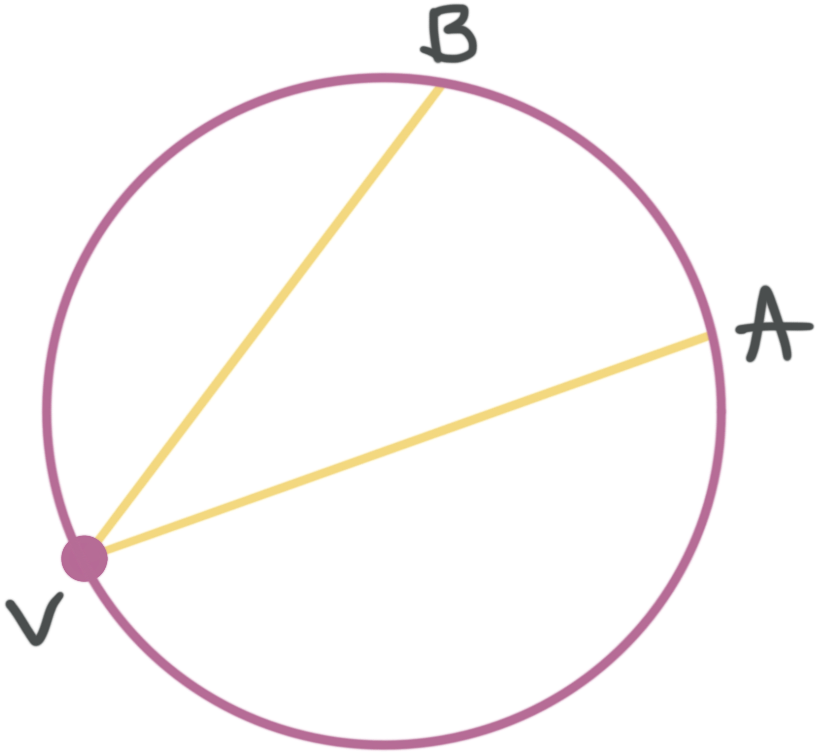
Angle ???AVB??? is an inscribed angle and arc ???AB??? is the intercepted arc.

Measures of inscribed angles, central angles and intercepted arcs

The measure of an intercepted arc is equal to the measure of its central angle.

The measure of an inscribed angle is equal to half the measure of the central angle that goes with the intercepted arc.

The measure of an inscribed angle is equal to half the measure of its intercepted arc.

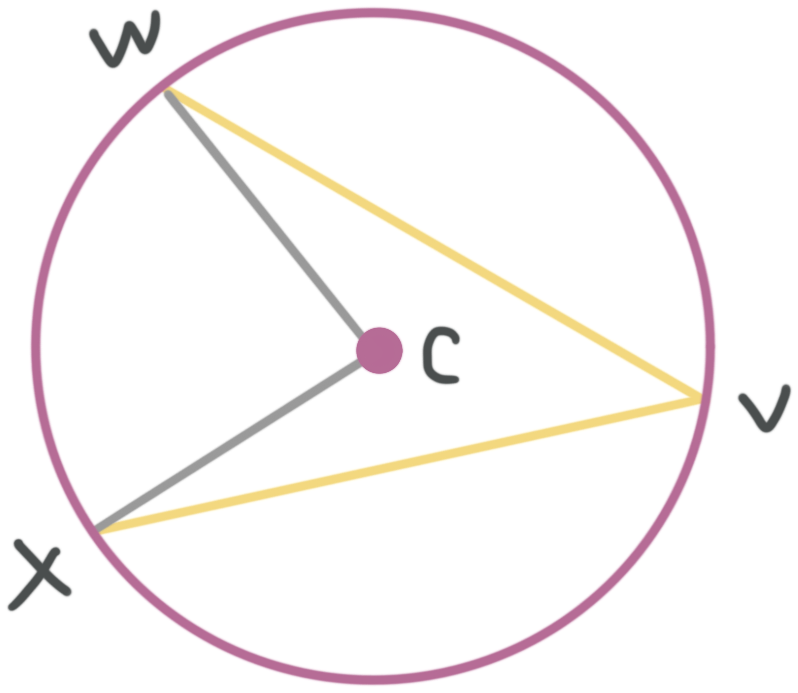
???m\text{ arc }{WX}=m\angle WCX???

???\frac{1}{2}m\angle WCX=m\angle WVX???

???\frac{1}{2}m\text{ arc }{WX}=m\angle WVX???

We can do some algebra to show that the following is also true.

???m\angle WCX=\frac{1}{2}m\text{ arc }{WX}=\angle WCX=2m\angle WVX???

Calculating measurements of inscribed angles in circles

Take the course

Want to learn more about Geometry? I have a step-by-step course for that. :)

Learn More

Calculating measures of inscribed angles

Example

Find the measure of the inscribed angle ???WVX??? if ???m\angle WCX=88^\circ???.

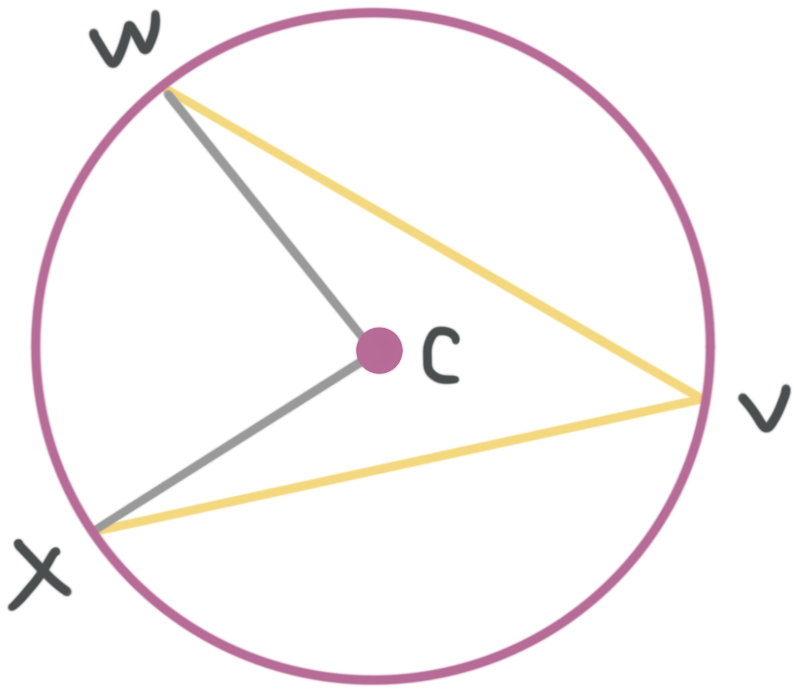
???\angle WCX??? is the central angle for the intercepted arc ???WX???. This means the inscribed angle measures half of the measure of ???\angle WCX???. We know

???\frac{1}{2}m\angle WCX=m\angle WVX???

and

???m\angle WCX=88^\circ???

So

???\frac{1}{2}(88^\circ )=m\angle WVX???

???44^\circ =m\angle WVX???

Let’s do a problem with a few more steps.

Example

Solve for ???x???.

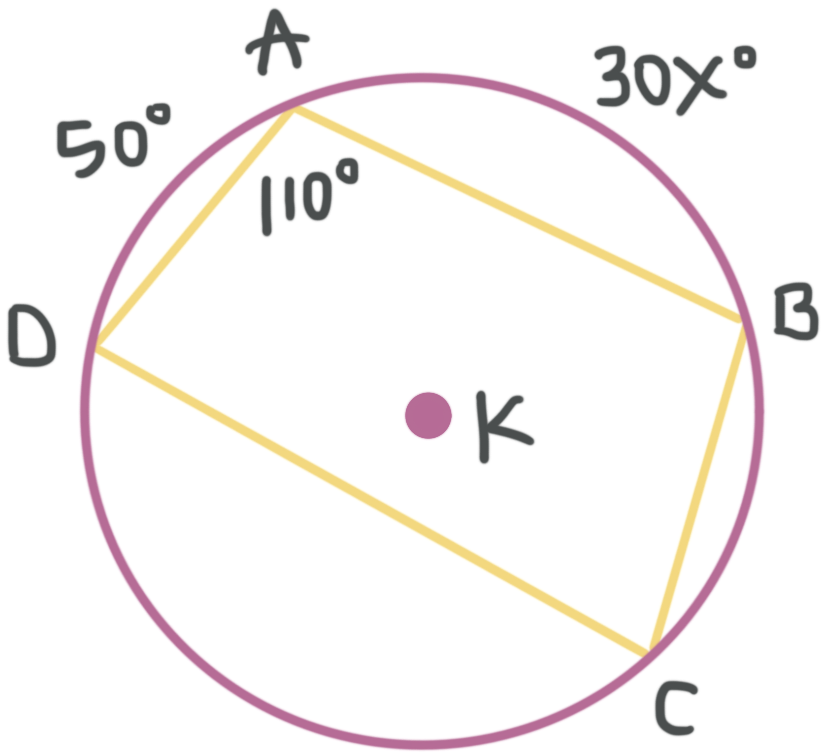
The full circle is ???360^\circ???. If we can find the measure of arc ???DB???, we can set up an equation to solve for ???x???, because ???m\text{ arc }{DB}+m\text{ arc }{BA}+m\text{ arc }{AD}=360^\circ???, and we know that ???m\text{ arc }{BA}=30x??? and ???m\text{ arc }{AD}=50^\circ???.

From the diagram we can see that ???m\angle DAB=110{}^\circ???. The intercepted arc that belongs to this angle is arc ???DB???. The intercepted arc has a measure of twice the inscribed angle.

???m\text{ arc }{DB}=2m\angle DAB=2(110^\circ )???

???m\text{ arc }{DB}=220^\circ???

Now we can use the equation we wrote earlier to solve for ???x???.

???m\text{ arc }{DB}+m\text{ arc }{BA}+m\text{ arc }{AD}=360^\circ???

???220^\circ +30x+50^\circ =360^\circ???

???270^\circ +30x=360^\circ???

???30x=90^\circ???

???x=3^\circ???

Get access to the complete Geometry course

Get started Learn mathKrista KingApril 2, 2021math, learn online, online course, online math, geometry, circles, inscribed angles of circles, inscribed angles, chords, inscribed angles in circles, geometry of circles, central angles, intercepted arcs Facebook0 Twitter LinkedIn0 Reddit Tumblr Pinterest0 0 Likes Previous

How to do long division with polynomials

Learn mathKrista KingApril 3, 2021math, learn online, online course, online math, algebra, algebra 2, algebra ii, polynomial long division, long division of polynomials, simplifying rational functions, simplifying rational expression, rational functions, rational expressions, long division, divide multiply subtract bring down Next

Representing repeating decimals as a ratio of integers using a geometric series

Learn mathKrista KingApril 1, 2021math, learn online, online course, online math, calculus 2, calculus ii, calc 2, calc ii, single variable calculus, single variable calc, sequences, series, sequences and series, infinite series, geometric series, repeating decimals, geometric series for repeating decimals, ratio of integers