Logarithmic Functions - Formula, Domain, Range, Graph - Cuemath

Logarithmic Functions

The logarithmic function is an important medium of math calculations. Logarithms were discovered in the 16th century by John Napier a Scottish mathematician, scientist, and astronomer. It has numerous applications in astronomical and scientific calculations involving huge numbers. Logarithmic functions are closely related to exponential functions and are considered as an inverse of the exponential function. The exponential function ax = N is transformed to a logarithmic function logaN = x.

The logarithm of any number N if interpreted as an exponential form, is the exponent to which the base of the logarithm should be raised, to obtain the number N. Here we shall aim at knowing more about logarithmic functions, types of logarithms, the graph of the logarithmic function, and the properties of logarithms.

1.	What are Logarithmic Functions?
2.	Domain and Range of Log Functions
3.	Logarithmic Graph
4.	Graphing Logarithmic Functions
5.	Properties of Logarithmic Functions
6.	Derivative and Integral of Logarithmic Functions
7.	FAQs on Logarithmic Functions

What are Logarithmic Functions?

The basic logarithmic function is of the form f(x) = logax (r) y = logax, where a > 0. It is the inverse of the exponential function ay = x. Log functions include natural logarithm (ln) or common logarithm (log). Here are some examples of logarithmic functions:

• f(x) = ln (x - 2)
• g(x) = log2 (x + 5) - 2
• h(x) = 2 log x, etc.

Some of the non-integral exponent values can be calculated easily with the use of logarithmic functions. Finding the value of x in the exponential expressions 2x = 8, 2x = 16 is easy, but finding the value of x in 2x = 10 is difficult. Here we can use log functions to transform 2x = 10 into logarithmic form as log210 = x and then find the value of x. The logarithm counts the number of occurrences of the base in repeated multiples. The formula for transforming an exponential function into a logarithmic function is as follows.

The exponential function of the form ax = N can be transformed into a logarithmic function logaN = x. The logarithms are generally calculated with a base of 10, and the logarithmic value of any number can be found using a Napier logarithm table. The logarithms can be calculated for positive whole numbers, fractions, decimals, but cannot be calculated for negative values.

Domain and Range of Log Functions

Let us consider the basic (parent) common logarithmic function f(x) = log x (or y = log x). We know that log x is defined only when x > 0 (try finding log 0, log (-1), log (-2), etc using your calculator. You will come up with an error). So the domain is the set of all positive real numbers. Now, we will observe some of the y-values (outputs) of the function for different x-values (inputs).

• When x = 1, y = log 1 = 0
• When x = 2, y = log 2 = 0.3010
• When x = 0.2, y = -0.6990
• When x = 0.01, y = -2, etc

We can see that y can be either a positive or negative real number (or) it can be zero as well. Thus, y can take the value of any real number. Hence, the range of a logarithmic function is the set of all real numbers. Thus:

• The domain of log function y = log x is x > 0 (or) (0, ∞).
• The range of any log function is the set of all real numbers (R)

Example: Find the domain and range of the logarithmic function f(x) = 2 log (2x - 4) + 5.

Solution:

For finding domain, set the argument of the function greater than 0 and solve for x.

2x - 4 > 0 2x > 4 x > 2

Thus, domain = (2, ∞).

As we have seen earlier, the range of any log function is R. So the range of f(x) is R.

Logarithmic Graph

We have already seen that the domain of the basic logarithmic function y = loga x is the set of positive real numbers and the range is the set of all real numbers. We know that the exponential and log functions are inverses of each other and hence their graphs are symmetric with respect to the line y = x. Also, note that y = 0 when x = 0 as y = loga1 = 0 for any 'a'. Thus, all such functions have an x-intercept of (1, 0). A logarithmic function doesn't have a y-intercept as loga0 is not defined. Summarizing all these, the graphs of exponential functions and logarithmic graph look like below.

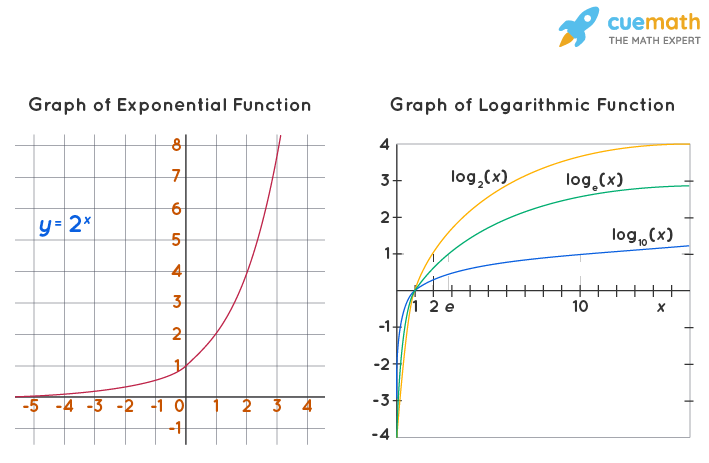
Properties of Logarithmic Graph

• a > 0 and a ≠ 1
• The logarithmic graph increases when a > 1, and decreases when 0 < a < 1.
• The domain is obtained by setting the argument of the function greater than 0.
• The range is the set of all real numbers.

Graphing Logarithmic Functions

Before drawing a log function graph, just have an idea of whether you get an increasing curve or decreasing curve as the answer. If the base > 1, then the curve is increasing; and if 0 < base < 1, then the curve is decreasing. Here are the steps for graphing logarithmic functions:

• Find the domain and range.
• Find the vertical asymptote by setting the argument equal to 0. Note that a log function doesn't have any horizontal asymptote.
• Substitute some value of x that makes the argument equal to 1 and use the property loga 1 = 0. This gives us the x-intercept.
• Substitute some value of x that makes the argument equal to the base and use the property loga a = 1. This would give us a point on the graph.
• Join the two points (from the last two steps) and extend the curve on both sides with respect to the vertical asymptote.

Example: Graph the logarithmic function f(x) = 2 log3 (x + 1).

Solution:

Here, the base is 3 > 1. So the curve would be increasing.

For domain: x + 1 > 0 ⇒ x > -1. So domain = (-1, ∞).

Range = R.

Vertical asymptote is x = -1.

• At x = 0, y = 2 log3 (0 + 1) = 2 log3 1 = 2 (0) = 0
• At x = 2, y = 2 log3 (2 + 1)= 2 log3 3 = 2 (1) = 2

If we want more clarity, we can form a table of values with some random values of x and substitute each of them in the given function to compute the y-values. This way, we get more points on the graph and it helps in getting the perfect shape of the graph.

Thus, (0, 0) and (2, 2) are two points on the curve. Thus, the log function graph looks as follows.

Properties of Logarithmic Functions

Logarithmic function properties are helpful to work across complex log functions. All the general arithmetic operations across numbers are transformed into a different set of operations within logarithms. The product of two numbers, when taken within the logarithmic functions is equal to the sum of the logarithmic values of the two functions. Similarly, the operations of division are transformed into the difference of the logarithms of the two numbers. Let us list the important properties of log functions in the below points.

• log ab = log a + log b
• loga/b = log a - log b
• logba = (logc a)/(logc b) (change of base rule)
• logax = x loga
• loga 1 = 0
• loga a = 1

Derivative and Integral of Logarithmic Functions

The derivation of the logarithmic function gives the slope of the tangent to the curve representing the logarithmic function. The formula for the derivative of the common and natural logarithmic functions are as follows.

• The derivative of ln x is 1/x. i.e., d/dx. ln x = 1/x.
• The derivative of logₐ x is 1/(x ln a). i.e., d/dx (logₐ x) = 1/(x ln a).

The integral formulas of logarithmic functions are as follows:

• The integral of ln x is ∫ ln x dx = x (ln x - 1) + C.
• The integral of log x is ∫ log x dx = x (log x - 1) + C.

Related Topics:

• Exponents
• Exponent Rules
• Properties of Logarithms
• Logs in calculations