Meaning, Examples | Y Intercept Formula - Cuemath

Y Intercept

The y-intercept is the point where the graph intersects the y-axis. To graph, any function that is of the form y = f(x) finding the intercepts is really important. There are two types of intercepts that a function can have. They are the x-intercept and the y-intercept. An intercept of a function is a point where the graph of the function cuts the axis.

Let us understand the meaning of the y-intercept along with its formula and examples.

1.	What is Y-Intercept?
2.	Y-Intercept Formula
3.	Y-Intercept of a Straight Line
4.	How To Find The Y-Intercept?
5.	Y-Intercept of a Quadratic Function (Parabola)
6.	FAQs on Y-Intercept

What is Y Intercept?

The y intercept of a graph is the point where the graph intersects the y-axis. We know that the x-coordinate of any point on the y-axis is 0. So the x-coordinate of a y-intercept is 0.

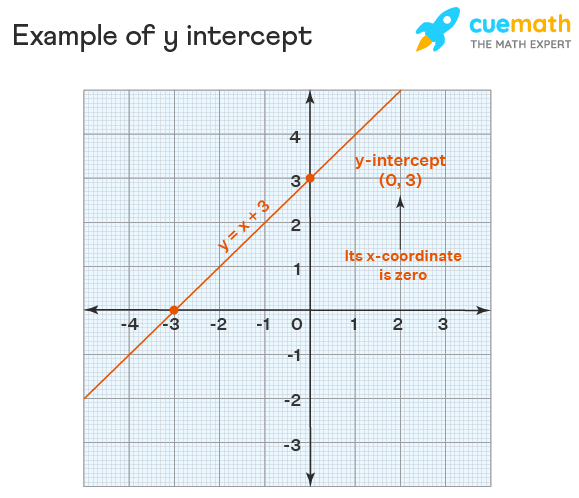
Here is an example of a y-intercept. Consider the line y = x+ 3. This graph meets the y-axis at the point (0,3). Thus (0,3) is the y-intercept of the line y = x+ 3.

Y-Intercept Formula

The y-intercept of a function is a point where its graph would meet the y-axis. The x-coordinate of any point on the y-axis is 0 and we use this fact to derive the formula to find the y-intercept. i.e., the y-intercept of a function is of the form (0, y). Thus, the formula to find the y-intercept is:

Y Intercept Formula

Here are the steps to find the y intercept of a function y = f(x),

• we just substitute x = 0 in it.
• solve for y.
• represent the y-intercept as the point (0, y).

Here are some examples of y intercepts.

• The y-intercept of y = 5x2 + 2 is, (0, 2) because when we substitute x = 0, we get y = 5(0)2 + 2 = 2.
• The y-intercept of y = -5ex is (0, -5) because when we substitute x = 0, we get y = -5e0 = -5.

Y-Intercept of a Straight Line

A straight line can be horizontal or vertical or slanting. The y intercept of a horizontal line with equation y = a is (0, a) and the y intercept of a vertical line does not exist. Let us learn to find the y intercept of a straight line represented in different forms.

Y-Intercept in General Form

The equation of a straight line in general form is ax+by+c=0. For y-intercept, we substitute x=0 and solve it for y.

a(0)+ by + c =0

by + c =0

y = - c/b

Thus, the y-intercept of the equation of a line in general form is:(0, -c/b) or -c/b

y-Intercept in Slope-Intercept Form

The equation of the line in the slope-intercept form is, y=mx+b. By the definition of the slope-intercept form itself, b is the y-intercept of the line. You try by substituting x=0 in y=mx+b and see whether you get b as the y-intercept. Thus, the y-intercept of the equation of a line in the slope-intercept form is (0, b) or b.

y-Intercept in Point-Slope Form

The equation of the line in the point-slope form is, y-y₁=m x-x₁. For y-intercept, we substitute x=0 and solve it for y.

y-y₁ = m (0-x₁ )

y-y₁= - mx₁

y = y₁ - mx₁

Thus, the y-intercept of the equation of a line in the point-slope form is: (0, y₁ - mx₁) or y₁ - mx₁

How To Find Y-Intercept?

We have derived the formulas to find the y-intercept of a line where the equation of the straight line is in different forms. In fact, we do not need to apply any of these formulas to find the y-intercept of a straight line. The y-intercept of the polynomial function of the form y = a1xn + a2 xn-1+ ... + an is just its constant term an (or) (0, an).

We just substitute x=0 in the equation of the line and solve for y. Then the corresponding y-intercept is y or (0, y).

Equation of Line	Substitute x=0 and solve for y	y intercept
3x+5y -6=0	3(0)+5y-6 =0 5y-6=0 y=6/5	6/5 (or) (0, 6/5)
y= 2x-3	y=2(0)-3=-3	-3 (or) (0, -3)

The y-intercept of a function can be easily found by graphing it using the graphing calculator and locating the point where the graph cuts the y-axis. A function has only one y-intercept because otherwise, it fails the vertical line test. The y-intercept of the second equation of the table (y = 2x - 3) is shown in the graph below.

Y-Intercept of a Quadratic Function (Parabola)

The procedure for finding the y-intercept of a quadratic function or the y-intercept of a parabola is the same as that of a line (as discussed in the previous section). If a quadratic equation is given, substitute x = 0 and solve for y to get the y intercept.

Examples

Equation of Parabola	Substitute x=0 and solve for y	y-Intercept
y= x2 -2x -3	y=02-2(0)-3=-3	-3 (or) (0, -3)
y= 2x2+5x-3	y=2(0)2+5(0)-3=-3	-3 (or) (0, -3)

Important Notes on y-Intercept

• We substitute x=0 and solve for y to find the y-intercept.
• In the same way, we substitute y=0 and solve for x to find the x-intercept.
• The lines parallel to the y-axis cannot have y-intercepts as they do not intersect the y-axis anywhere.
• The y-intercept of a line is widely used as an initial point while graphing a line by plotting two points.
• A function has cannot have more than one y-intercept.

☛ Related Topics:

• Y-Intercept Calculator
• X-Intercept Formula
• X-Intercept Calculator