Measures Of Parallelograms, Including Angles, Sides, And Diagonals

About Pricing Login Subscribe Risk Free Measures of parallelograms, including angles, sides, and diagonals

Defining all the measures of a parallelogram

A parallelogram is a quadrilateral that has opposite sides that are parallel.

The parallel sides let you know a lot about a parallelogram.

Here are the special properties of parallelograms:

Parallelogram

Two pairs of opposite parallel sides

Opposite sides are equal lengths

Opposite angles are congruent

???m\angle 1=m\angle 3???

???m\angle 2=m\angle 4???

Consecutive angles are supplementary

???m\angle 1+m\angle 2=180^\circ???

???m\angle 2+m\angle 3=180^\circ???

???m\angle 3+m\angle 4=180^\circ???

???m\angle 4+m\angle 1=180^\circ???

Diagonals bisect each other (cut each other in half)

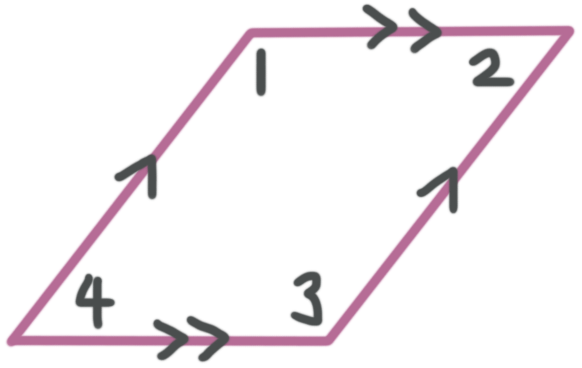
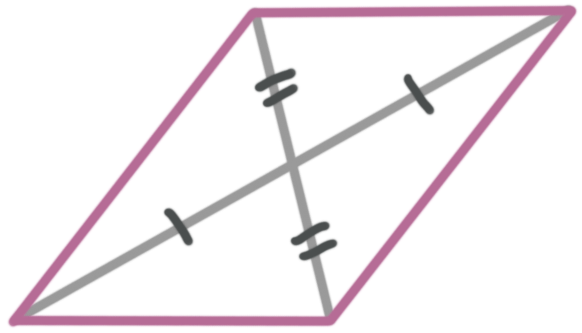
How to solve for every measure of a parallelogram, including angles, side lengths, and the lengths of diagonals

Take the course

Want to learn more about Geometry? I have a step-by-step course for that. :)

Learn More

Finding the measure of a interior angle of a parallelogram

Example

Find the measure of angle ???y???, given ???JKLM??? is a parallelogram.

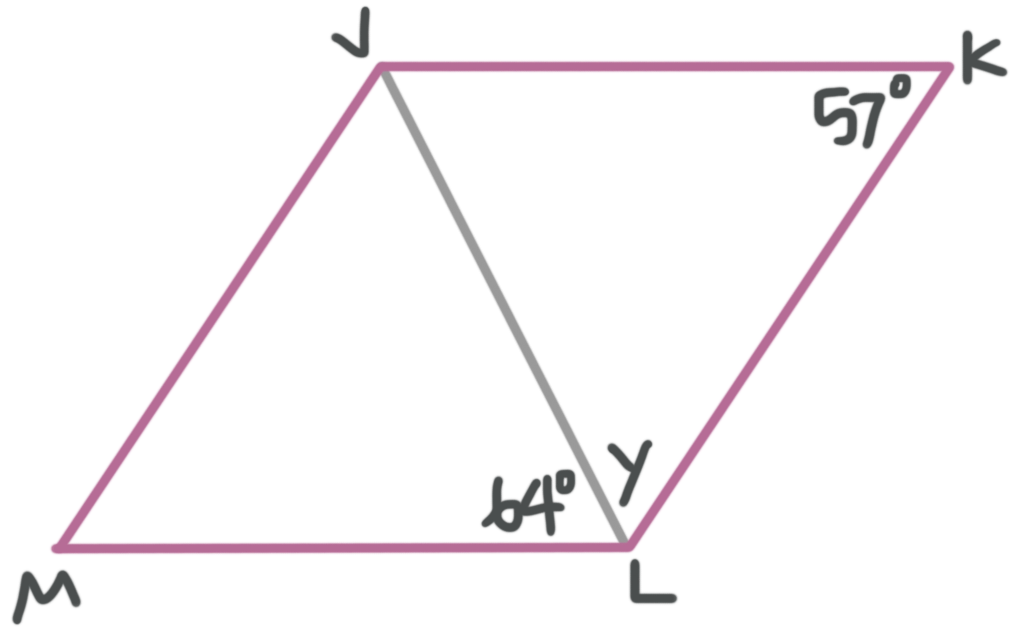
Opposite angles of parallelograms are congruent, so

???m\angle JML=m\angle JKL=57^\circ???

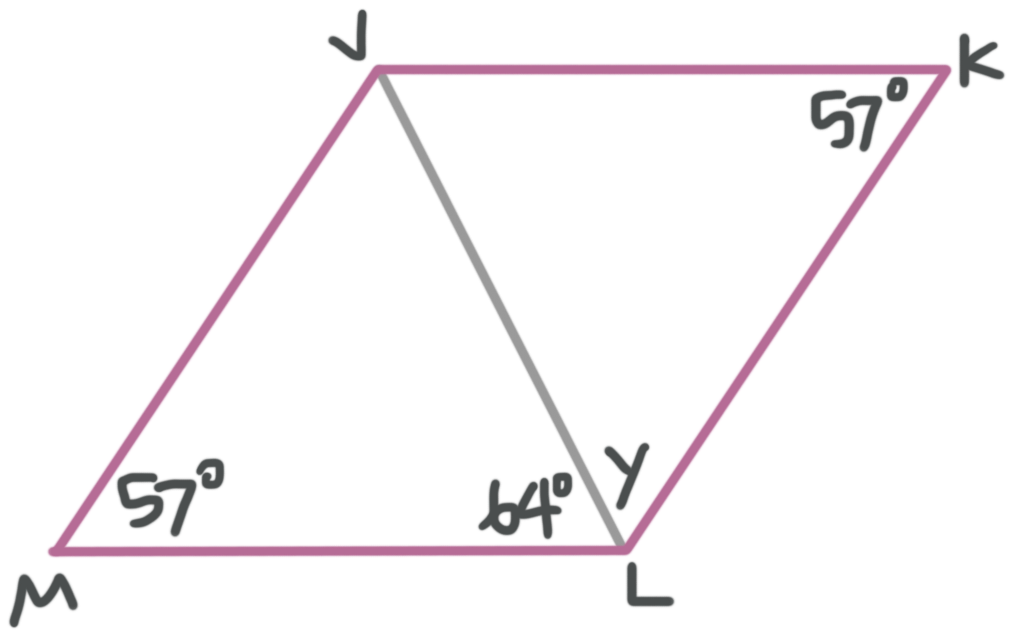
Now we can use the fact that opposite sides of a parallelogram are parallel to state that ???JK\parallel ML???. This means that the diagonal ???JL??? of the parallelogram is also a transversal of these two parallel lines. This means that ???\angle KLJ??? and ???\angle MJL??? are alternate interior angles. Alternate interior angle pairs are congruent, so ???m\angle KLJ=m\angle MJL=y???.

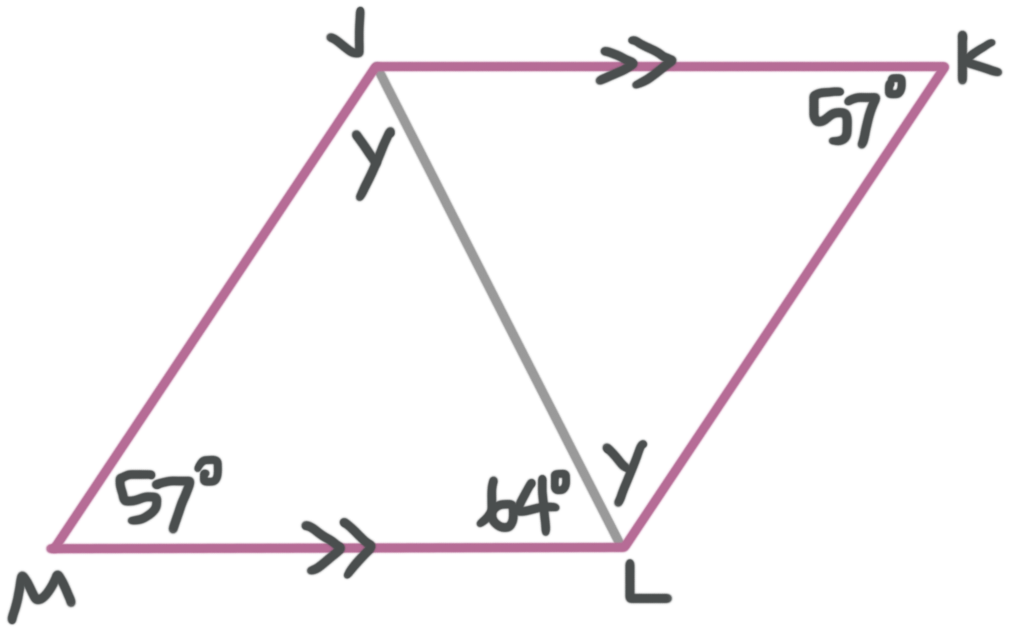
The measures of the three interior angles of a triangle add up to ???180^\circ???, so we can set up an equation for the sum of the interior angles of ???\triangle JML??? and solve for ???y???.

???y+57^\circ+64^\circ=180^\circ???

???y=59^\circ???

Example

If ???STUV??? is a parallelogram, and if ???VT=4n+34??? and ???VE=7n-3???, what is the length of ???ET????

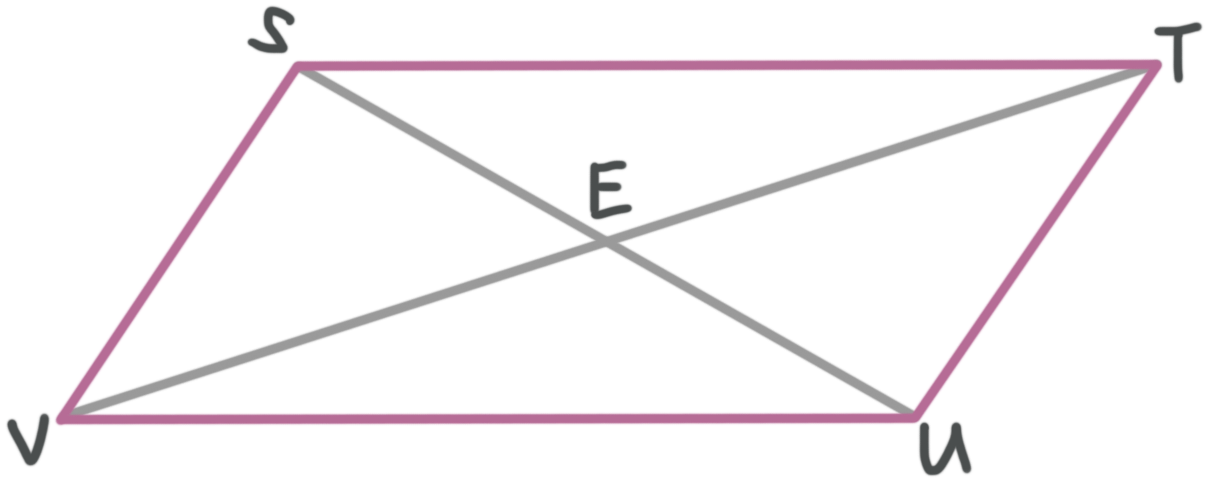
We know that the diagonals of a parallelogram bisect each other. Let’s add this information into the diagram.

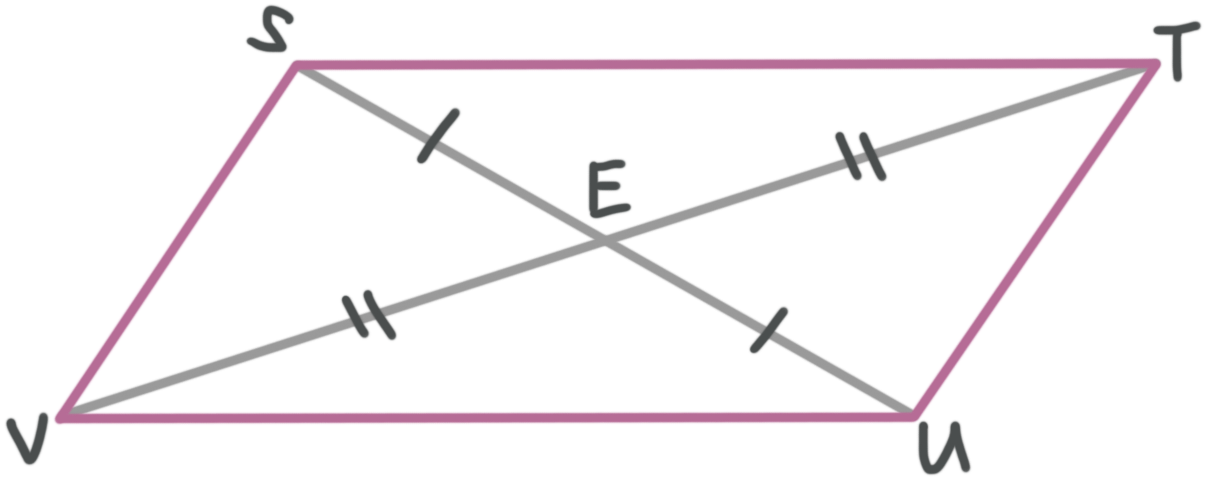
Now we can see the relationships we need. Because the diagonals bisect, ???VE=ET??? and ???VE=(1/2)VT???. We can use what we know to find the length of ???VE??? and then we’ll know the length of ???ET??? as well.

???VE=\frac{1}{2}VT???

???7n-3=\frac{1}{2}(4n+34)???

???7n-3=2n+17???

???5n=20???

???n=4???

Now we can substitute back in to find the length of ???VE???, which is equal to the length of ???ET???.

???VE=ET=7n-3???

???VE=ET=7(4)-3???

???VE=ET=25???

Get access to the complete Geometry course

Get started Learn mathKrista KingNovember 16, 2020math, learn online, online course, online math, geometry, parallelograms, measures of parallelograms, angles of a parallelogram, sides of a parallelogram, side lengths of a parallelogram, diagonals of a parallelogram, parallel sides, equivalent angles, equal angles, bisecting diagonals Facebook0 Twitter LinkedIn0 Reddit Tumblr Pinterest0 0 Likes Previous

Solving half-life problems with exponential decay

Learn mathKrista KingNovember 16, 2020math, learn online, online course, online math, calculus 1, calculus i, calc 1, calc i, applications of derivatives, derivatives, differentiation, applications of differentiation, derivative applications, half life, exponential growth, exponential decay, decay equation, growth equation, decay constant, growth constant, substance, half of the original substance, amount of substance remaining Next

Solving proportions of complex fractions with cross multiplication

Learn mathKrista KingNovember 16, 2020math, learn online, online course, online math, algebra, algebra 2, algebra ii, cross multiplication, complex fractions, ratios, proportions, ratio and proportion, solving proportions, fraction multiplication