Parabolas With Vertices Not At The Origin | College Algebra

Skip to main content College Algebra

Module 15: Conic Sections

Search for:

Parabolas with Vertices Not at the Origin

Learning Outcomes

• Identify and label the vertex, axis of symmetry, focus, directrix, and endpoints of the focal diameter given the equation of a parabola in standard form.
• Find the equation of a parabolic shaped object given dimensions.

Like other graphs we’ve worked with, the graph of a parabola can be translated. If a parabola is translated [latex]h[/latex] units horizontally and [latex]k[/latex] units vertically, the vertex will be [latex]\left(h,k\right)[/latex]. This translation results in the standard form of the equation we saw previously with [latex]x[/latex] replaced by [latex]\left(x-h\right)[/latex] and [latex]y[/latex] replaced by [latex]\left(y-k\right)[/latex].

To graph parabolas with a vertex [latex]\left(h,k\right)[/latex] other than the origin, we use the standard form [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex] for parabolas that have an axis of symmetry parallel to the x-axis, and [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex] for parabolas that have an axis of symmetry parallel to the y-axis. These standard forms are given below, along with their general graphs and key features.

A General Note: Standard Forms of Parabolas with Vertex (h, k)

The table summarizes the standard features of parabolas with a vertex at a point [latex]\left(h,k\right)[/latex].

Axis of Symmetry	Equation	Focus	Directrix	Endpoints of focal diameter
[latex]y=k[/latex]	[latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex]	[latex]\left(h+p,\text{ }k\right)[/latex]	[latex]x=h-p[/latex]	[latex]\left(h+p,\text{ }k\pm 2p\right)[/latex]
[latex]x=h[/latex]	[latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex]	[latex]\left(h,\text{ }k+p\right)[/latex]	[latex]y=k-p[/latex]	[latex]\left(h\pm 2p,\text{ }k+p\right)[/latex]

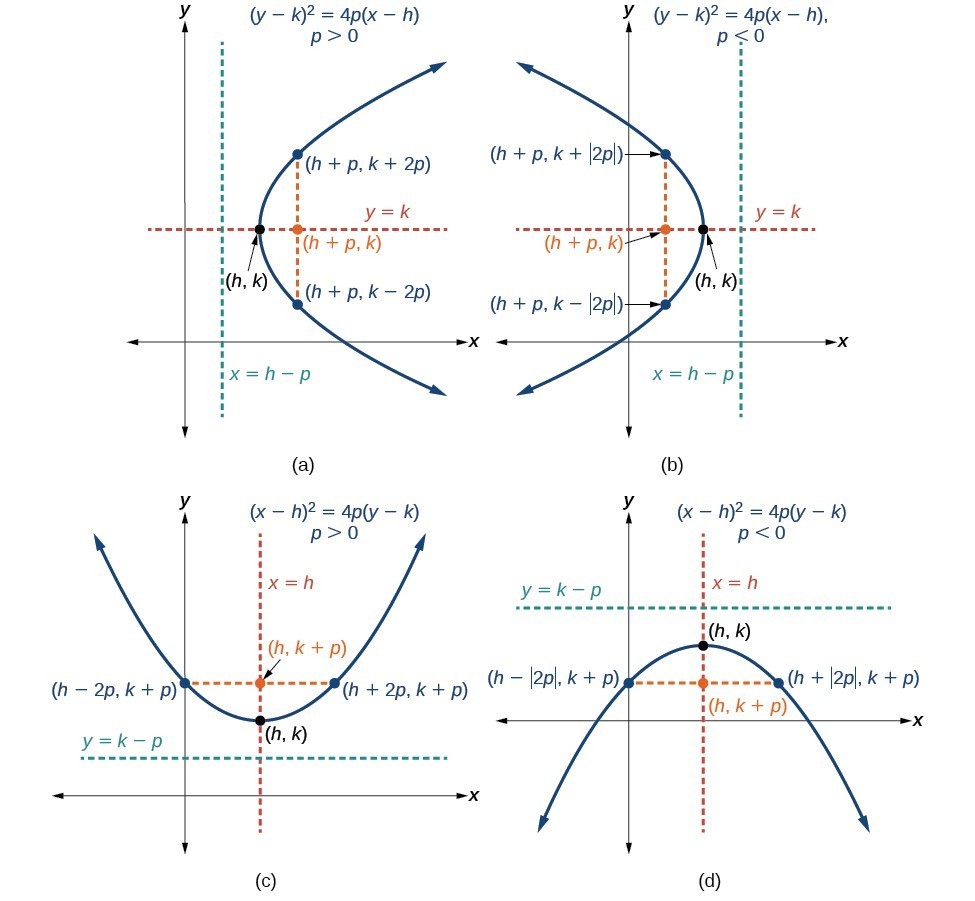
(a) When [latex]p>0[/latex], the parabola opens right. (b) When [latex]p<0[/latex], the parabola opens left. (c) When [latex]p>0[/latex], the parabola opens up. (d) When [latex]p<0[/latex], the parabola opens down.

How To: Given a standard form equation for a parabola centered at (h, k), sketch the graph.

1. Determine which of the standard forms applies to the given equation: [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex] or [latex]{\left(x-h\right)}^{2}=4p\left(y-k\right)[/latex].
2. Use the standard form identified in Step 1 to determine the vertex, axis of symmetry, focus, equation of the directrix, and endpoints of the focal diameter.
   1. If the equation is in the form [latex]{\left(y-k\right)}^{2}=4p\left(x-h\right)[/latex], then:
      • use the given equation to identify [latex]h[/latex] and [latex]k[/latex] for the vertex, [latex]\left(h,k\right)[/latex]
      • use the value of [latex]k[/latex] to determine the axis of symmetry, [latex]y=k[/latex]
      • set [latex]4p[/latex] equal to the coefficient of [latex]\left(x-h\right)[/latex] in the given equation to solve for [latex]p[/latex]. If [latex]p>0[/latex], the parabola opens right. If [latex]p0[/latex], the parabola opens up. If [latex]p0[/latex]. The igniter, which is the focus, is 1.7 inches above the vertex of the dish. Thus we have [latex]p=1.7[/latex].

        [latex]\begin{align}&{x}^{2}=4py && \text{Standard form of upward-facing parabola with vertex (0,0)} \\ &{x}^{2}=4\left(1.7\right)y && \text{Substitute 1}\text{.7 for }p. \\ &{x}^{2}=6.8y && \text{Multiply}. \end{align}[/latex]

        The dish extends [latex]\frac{4.5}{2}=2.25[/latex] inches on either side of the origin. We can substitute 2.25 for [latex]x[/latex] in the equation from part (a) to find the depth of the dish.

        [latex]\begin{align}&{x}^{2}=6.8y && \text{Equation found in part (a)}. \\ &{\left(2.25\right)}^{2}=6.8y && \text{Substitute 2}\text{.25 for }x. \\ &y\approx 0.74 && \text{Solve for }y. \end{align}[/latex]

        The dish is about 0.74 inches deep.

        Try It

        Balcony-sized solar cookers have been designed for families living in India. The top of a dish has a diameter of 1600 mm. The sun’s rays reflect off the parabolic mirror toward the “cooker,” which is placed 320 mm from the base.

        1. Find an equation that models a cross-section of the solar cooker. Assume that the vertex of the parabolic mirror is the origin of the coordinate plane, and that the parabola opens to the right (i.e., has the x-axis as its axis of symmetry).
        2. Use the equation found in part (a) to find the depth of the cooker.
        Show Solution
        1. [latex]{y}^{2}=1280x[/latex]
        2. The depth of the cooker is 500 mm

        Candela Citations

        CC licensed content, Original
        • Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
        CC licensed content, Shared previously
        • College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/[email protected]. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/[email protected]
        • Question ID 86148, 86124, 87082. Authored by: Shahbazian, Roy. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
        CC licensed content, Specific attribution
        • Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution
        Licenses and Attributions CC licensed content, Original
        • Revision and Adaptation. Provided by: Lumen Learning. License: CC BY: Attribution
        CC licensed content, Shared previously
        • College Algebra. Authored by: Abramson, Jay et al.. Provided by: OpenStax. Located at: http://cnx.org/contents/[email protected]. License: CC BY: Attribution. License Terms: Download for free at http://cnx.org/contents/[email protected]
        • Question ID 86148, 86124, 87082. Authored by: Shahbazian, Roy. License: CC BY: Attribution. License Terms: IMathAS Community License CC-BY + GPL
        CC licensed content, Specific attribution
        • Precalculus. Authored by: OpenStax College. Provided by: OpenStax. Located at: http://cnx.org/contents/[email protected]:1/Preface. License: CC BY: Attribution
        Previous Next