Perimeter Of Parallelogram - Formula, Definition, Examples ...

Perimeter of Parallelogram

The perimeter of a parallelogram is the length of the continuous line formed by its boundary. Its unit is the same as that of its sides. A quadrilateral is a closed shape made up of four line segments. A quadrilateral is called a parallelogram if its opposite sides are parallel and are of equal length. Some examples of a parallelogram are rhombus, rectangle, and square. Here are some properties of a parallelogram. In simple words, we can say that the perimeter of a parallelogram is equal to the sum of all its four sides.

• Opposite sides are equal.
• Opposite angles are equal.
• Diagonals bisect each other.
• Every two adjacent angles are supplementary.

In this article, we will learn how to find the perimeter of a parallelogram using some formulas. We shall also understand the applications of the perimeter of parallelogram formulas. We will explore the concept with the help of a few solved examples for a better understanding of the concept.

1.	What Is the Perimeter of Parallelogram?
2.	Perimeter of Parallelogram Formula
3.	Perimeter of Parallelogram Formula With Sides
4.	Perimeter of Parallelogram Formula With One Side and Diagonals
5.	Perimeter of Parallelogram Base,Height,and Angle
6.	Find the Perimeter of Parallelogram
7.	FAQs on Perimeter of Parallelogram

What Is the Perimeter of Parallelogram?

The perimeter of a parallelogram is the length of its outline and hence it is equal to the sum of all its sides. But we always might not know all the sides of a parallelogram. Instead, we may be given other information about the parallelogram and are asked to find its perimeter. So, we have different formulas to find the perimeter of a parallelogram using its different components. In the next section, let us go through its various formulas to find the perimeter of the parallelogram.

Perimeter of Parallelogram Formula

The perimeter of a parallelogram can be found in the following cases:

• When two adjacent sides are known.
• When one side and diagonals are known.
• When base, height, and any angle are known.

Here are the formulas to find the perimeter of a parallelogram in each of these cases:

• P = 2 (a + b), where a, b are the adjacent sides of a parallelogram
• P = 2a + √(2x2 + 2y2 - 4a2), where a is the a side of the parallelogram, and x, y are its diagonals.
• P = 2a + 2h / sinθ, where a is the side of the parallelogram, h is the height and θ is the angle of the parallelogram.

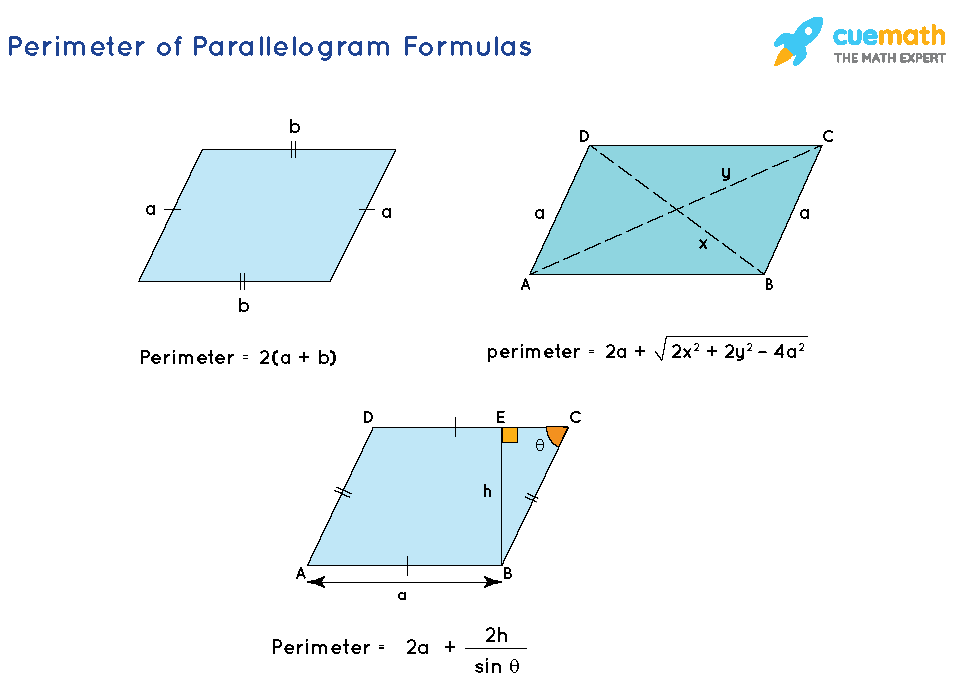
But how to derive all these formulas? Let us now derive the given formulas to find the perimeter of a parallelogram.

Perimeter of Parallelogram Formula With Sides

As discussed earlier, the perimeter of a parallelogram is the sum of the lengths of all its sides. We know that the opposite sides of a parallelogram are equal. Let us consider a parallelogram with two adjacent sides to be 'a' and 'b' (then the other two adjacent sides also will be 'a' and 'b' only).

Then the perimeter of the parallelogram is a + b + a + b (or) 2a + 2b (or) 2 (a + b). Thus, the perimeter (P) of a parallelogram with sides a and b is,

P = 2 (a + b) units.

Perimeter of Parallelogram Formula With One Side and Diagonals

Let us consider a parallelogram with sides 'a' and 'b' and diagonals 'x' and 'y'. Assume that the values of the side 'a', and the diagonals 'x' and 'y' are given but the value of 'b' is not given and we are asked to find the perimeter of the parallelogram.

Applying the law of cosines for the triangle ABD,

x2 = a2 + b2 - 2ab cos ∠BAD

Applying the cosine rule for the triangle ADC,

y2 = a2 + b2 - 2ab cos ∠ADC

Adding the above two equations,

x2 + y2 = 2a2 + 2b2 - 2ab (cos ∠BAD + cos ∠ADC) .... (1)

We know that any two adjacent angles of a parallelogram (it is a property of parallelograms) are supplementary. So

∠BAD + ∠ADC = 180°

∠BAD = 180° - ∠ADC

Applying cos on both sides,

cos ∠BAD = cos (180° - ∠ADC) = - cos ∠ADC

Substituting this in (1),

x2 + y2 = 2a2 + 2b2 - 2ab ( - cos ∠ADC + cos ∠ADC)

x2 + y2 = 2a2 + 2b2 - 2ab (0)

x2 + y2 = 2a2 + 2b2

We have got the relation between the sides and diagonals of the parallelogram. Now, we will solve it for 'b' as we are not given the length of 'b'.

2b2 = x2 + y2 - 2a2

b2 = (x2 + y2 - 2a2) / 2

b = √ [(x2 + y2 - 2a2) / 2]

Now we know the sides of the parallelogram ('a' and 'b') and hence we can use the formula from the previous section to find its perimeter (P).

P = 2a + 2b

P = 2a + 2 √ [(x2 + y2 - 2a2) / 2]

P = 2a + √[2(x2 + y2 - 2a2)

P = 2a + √(2x2 + 2y2 - 4a2)

Perimeter of Parallelogram With Base, Height, and Angle

Let us consider a parallelogram with one of the sides given to be 'a', its corresponding height given to be 'h', and one of the vertex angles given to be 'θ'. Let us assume that the unknown side of the parallelogram be 'b'. We will first solve for 'b' and then find the perimeter.

Applying sin to the triangle BEC,

sin θ = h/b

b = h / sin θ

Thus, the perimeter (P) of the parallelogram is,

P = 2a + 2b

P = 2a + 2h / sin θ

Here θ doesn't need to be a specific angle of the parallelogram. It can be any vertex angle because any two adjacent angles of a parallelogram are supplementary and sin θ = sin (180° - θ), for any θ.

Find the Perimeter of Parallelogram

Let us see the applications of the perimeter of parallelogram formulas in this section. We will go through some of the solved examples to understand how to find the perimeter using the formulas discussed the sections above.

Example 1: Find the perimeter of a parallelogram whose adjacent sides are 5 units and 9 units.

Solution: The adjacent sides of the given parallelogram are, a = 5 units and b = 9 units. Then its perimeter (P) is,

P = 2 (a + b)

P = 2 (5 + 9) = 2 (14) = 28 units.

Example 2: Find the perimeter of a parallelogram when one of its sides is 7 units and diagonals are 8 units and 10 units.

Solution: Using the formula when a side and diagonals of a parallelogram are given, we P = 2a + √(2x2 + 2y2 - 4a2). Here a = 7, x = 8, y = 10. Substituting these values into the formula, we have

P = 2a + √(2x2 + 2y2 - 4a2)

= 2 × 7 + √(2(8)2 + 2(10)2 - 4(7)2)

= 14 + √(2 × 64 + 2 × 100 - 4 × 49)

= 14 + √(128 + 200 - 196)

= 14 + √(132)

= 14 + 11.49

= 25.49 units (rounded to two decimal places)

Important Notes on Perimeter of Parallelogram

• The perimeter of a parallelogram is equal to the sum of all its four sides.
• We have three formulas to find the perimeter of a parallelogram with sides a, b; diagonals x, y, and angle θ.
  • P = 2 (a + b), where a, b are the adjacent sides of a parallelogram
  • P = 2a + √(2x2 + 2y2 - 4a2), where a is the a side of the parallelogram, and x, y are its diagonals.
  • P = 2a + 2h / sinθ, where a is the side of the parallelogram, h is the height and θ is the angle of the parallelogram.

☛ Related Articles:

• Parallelogram Formula
• Perimeter Formulas
• Difference Between Area and Perimeter