Pythagorean Triples - Definition, Formula, Examples - Cuemath

Pythagorean Triples

Pythagorean triples are any three positive integers that completely satisfy the Pythagorean theorem. The theorem states that in any right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two legs of the right triangle. These three sides of the right triangle form the Pythagorean triples. Let us learn how to generate a few Pythagorean triples in this article.

1.	What are Pythagorean Triples?
2.	Examples of Pythagorean Triples
3.	Pythagorean Triples Proof
4.	List of Pythagorean Triples
5.	FAQs on Pythagorean Triples

What are Pythagorean Triples?

Pythagorean triples are a set of 3 positive numbers that fit in the formula of the Pythagoras theorem which is expressed as, a2 + b2 = c2, where a, b, and c are positive integers. Here, 'c' is the 'hypotenuse' or the longest side of the triangle and 'a' and 'b' are the other two legs of the right-angled triangle. The Pythagorean triples are represented as (a,b, c). The most popular example of Pythagorean triples is (3, 4, 5). We can verify that 3, 4 and 5 satisfy the equation a2 + b2 = c2. Let us see how! 32 + 42 = 52 ⇒ 9 + 16 = 25. Observe the right-angled triangle given below which shows the Pythagorean triples, 3, 4, and 5.

Examples of Pythagorean Triples

The set of the Pythagorean triples is endless. The first known Pythagorean triples is (3, 4, and 5). We can generate a few more triples by scaling them up in the following manner. We can create as many triples as possible by taking values for n.

n	(3n, 4n, 5n)
2	(6, 8, 10)
3	(9, 12, 15)
4	(12, 16, 20)

Pythagorean Triples Proof

Let us consider Pythagorean triples (9, 40, 41) for which we can verify the Pythagorean formula (Hypotenuse2 = side 12 + side 22). The hypotenuse of the right-angled triangle is the longest side = 41

Hypotenuse2 = 412 = 1681

The other two sides of the right angled triangle = 9 and 40

side 12 + side 2 ⇒ 92 + 402 ⇒ 81 + 1600 = 1681

Thus, for any 3 Pythagorean Triples, we can verify the Pythagorean formula.

Tips and Tricks

• If we know one of the 3 triples, we can find the other two. If the given number (n) is an odd number, the Pythagorean triples are of the form, (n, (n2/2 - 0.5) and (n2/2 + 0.5)). For example, consider 5. The triples are (5, 25/2 - 0.5, 25/2 + 0.5) Finally, we get (5, 12 and 13)
• If the given number (n) is an even number, the Pythagorean triples are of the form = n, (n/2)2-1), ((n/2)2+1). For example, consider 6. The triples are (6, (3)2 - 1, (3)2 + 1) Finally, we get (6, 8, and 10)

List of Pythagorean Triples

The following table shows a list of a few Pythagorean Triples.

(3, 4, 5)	(5,12,13)	(7, 24, 25)
(8, 15, 17)	(9, 40, 41)	(11, 60, 61)
(12,35, 37)	(13, 84, 85)	(15, 112, 113)
(16, 63, 65)	(17,144, 145)	(19, 180, 181)
(20, 21, 29)	(20, 99 ,101)	(21, 220,221)

How to Generate Pythagorean Triples?

In order to generate Pythagorean triples, we use a formula, which is also known as the Pythagorean triple checker. Observe the figure given below and make the following assumptions where:

• a, b = legs of a right-angled triangle
• c = Hypotenuse of the right-angled triangle
• m, n are any two positive integers; and where m > n
• m and n are coprime numbers and both should not be odd numbers.

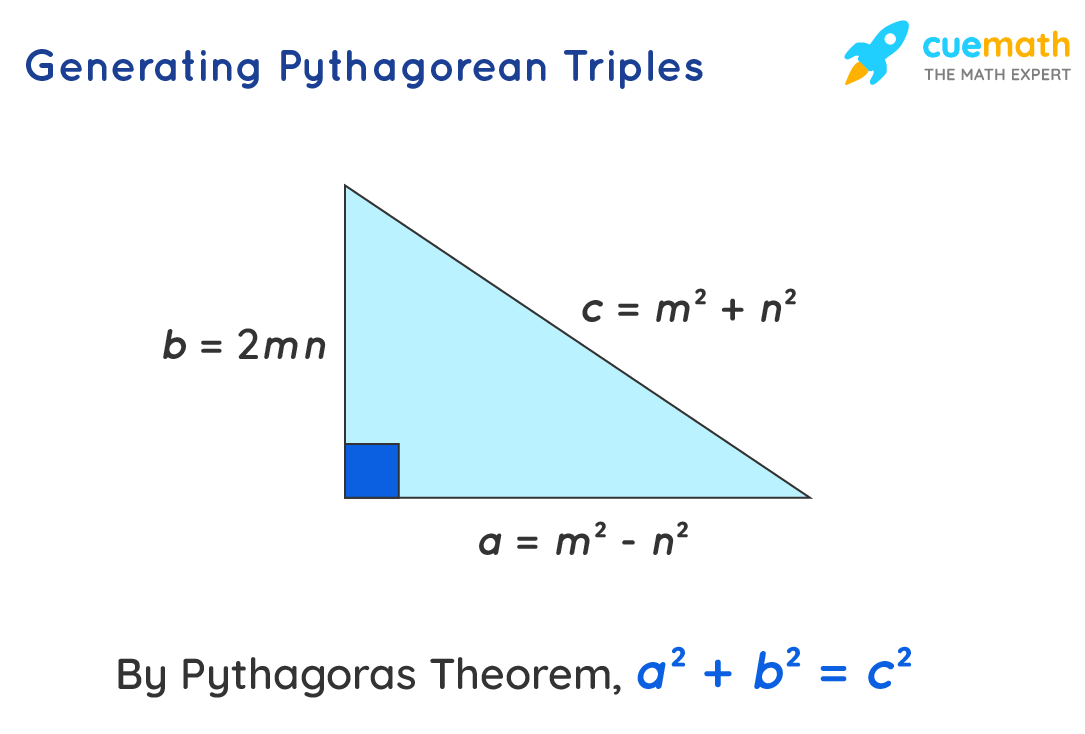
Let us assume any 2 integers 'm' and 'n', which will help us in generating the Pythagorean formula. Now, the lengths of our sides are a, b, and c. We will use 'm' and 'n' in order to find the exact values of the sides.

• The length of side 'a' is determined by defining the difference between the squares of 'm' and 'n' which is expressed as a = m2 - n2
• The length of side 'b' is determined by doubling the product of 'm' and 'n'. This makes it b = 2mn in the equation form.
• Finally, the length of side 'c' is computed by the sum of the squares of m and n. This can be expressed as c = m2 + n2

Now, we have concluded the following formulas:

• a = m2- n2
• b = 2mn
• c = m2+ n2

It is to be noted that any one of the formulas given above can be used based on the condition and the requirement of finding the Pythagorean triples. To generate random Pythagorean triples, consider random natural numbers m and n, such that m > n and determine the triples (a,b,c) such that a = m2- n2, b = 2mn, c = m2+ n2

Example: Let us generate Pythagorean triples using the two integers 2 and 3.

Solution: Since m > n, m = 3, and n = 2. Now that we know the values of m and n, let us substitute those values into the formulas of a, b, and c, to get the sides of the right triangle.

Computing a:

a = m2 - n2

a = 32 - 22

9 - 4 = 5

a = 5

Computing b:

b = 2mn

b = 2 × 3 × 2

b = 12

Computing c:

c = m2 + n2

c = 32 + 22

c = 13 Let us see if our values for a = 5, b = 12, and c = 13 satisfy the Pythagorean theorem, which is a2 + b2 = c2

LHS: 52 + 122 = 25 +144 = 169

RHS : 132 = 169 Yes, it does! Therefore, (5, 12, 13) are Pythagorean triples.

Important notes

• Any three positive integers which satisfy the Pythagorean theorem formula of a2 + b2 = c2 are known as Pythagorean triples.
• Pythagorean triples cannot be expressed in decimals.

☛ Related Articles

• Hypotenuse Leg Theroem
• Pythagorean Theorem Calculator
• Pythagorean Triples Calculator