Quotient Rule - Formula, Proof, Definition, Examples - Cuemath

Quotient Rule

Quotient rule in calculus is a method to find the derivative or differentiation of a function given in the form of a ratio or division of two differentiable functions. That means, we can apply the quotient rule when we have to find the derivative of a function of the form: f(x)/g(x), such that both f(x) and g(x) are differentiable, and g(x) ≠ 0. The quotient rule follows the product rule and the concept of limits of derivation in differentiation directly. Let us understand the formula for quotient rule, its proof using solved examples in detail in the following sections.

1.	What is Quotient Rule?
2.	Quotient Rule Formula
3.	Derivation of Quotient Rule Formula
4.	How to Apply the Quotient Rule in Differentiation?
5.	FAQs on Quotient Rule

What is the Quotient Rule?

Quotient rule in calculus is a method used to find the derivative of any function given in the form of a quotient obtained from the result of the division of two differentiable functions. The quotient rule in words states that the derivative of a quotient is equal to the ratio of the result obtained on the subtraction of the numerator times the derivative of the denominator from the denominator times the derivative of the numerator to the square of the denominator. That means if we are given a function of the form: f(x) = u(x)/v(x), we can find the derivative of this function using the quotient rule derivative as,

f'(x) = [u(x)/v(x)]' = [v(x) × u'(x) - u(x) × v'(x)]/[v(x)]2

Quotient Rule Formula

We can calculate the derivative or evaluate the differentiation of the quotient of two functions using the quotient rule derivative formula. The quotient rule derivative formula is given as,

f'(x) = [u(x)/v(x)]' = [v(x) × u'(x) - u(x) × v'(x)]/[v(x)]2

where,

• f(x) = The function of the form u(x)/v(x) for which the derivative is to be calculated.
• u(x) = A differentiable function that makes numerator of the function f(x).
• u'(x) = Derivative of function u(x).
• v(x) = A differentiable function that makes denominator of the given function f(x).
• v'(x) = Derivative of the function v(x).

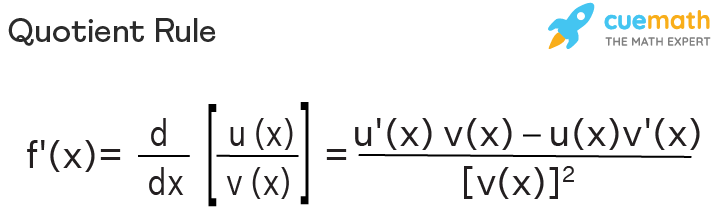
Derivation of Quotient Rule Formula

In the previous section, we learned about the quotient formula to find derivatives of the quotient of two differentiable functions. Let us see the proof of the quotient rule formula here. There are different methods to prove the quotient rule formula, given as,

• Using derivative and limit properties
• Using implicit differentiation
• Using chain rule

Quotient Rule Formula Proof Using Derivative and Limit Properties

To prove quotient rule formula using the definition of derivative or limits, let the function f(x) = u(x)/v(x).

⇒ f'(x) = \(\mathop {\lim }\limits_{h \to 0}\) [f(x + h) - f(x)]/h

= \(\mathop {\lim }\limits_{h \to 0}\) \(\frac{\frac{u(x+h)}{v(x+h)} - \frac{u(x)}{v(x)}}{h}\)

= \(\mathop {\lim }\limits_{h \to 0}\) \(\frac{u(x+h)v(x) - u(x)v(x+h)}{h \cdot v(x) \cdot v(x+h)}\)

= \( \left(\mathop {\lim }\limits_{h \to 0} \frac{u(x+h)v(x) - u(x)v(x+h)}{h}\right) \left(\mathop {\lim }\limits_{h \to 0} \frac{1}{v(x) \cdot v(x+h)}\right)\)

= \(\left(\mathop {\lim }\limits_{h \to 0} \frac{u(x+h)v(x) - u(x)v(x) + u(x)v(x) - u(x)v(x + h)}{h}\right) \) [1/v(x)2]

= \(\left[\!\left(\mathop {\lim }\limits_{h \to 0} \frac{u(x+h)v(x) - u(x)v(x)}{h}\right)\!\!\! -\!\! \left(\mathop {\lim }\limits_{h \to 0} \frac{u(x)v(x + h) - u(x)v(x)}{h}\right)\!\right]\) [1/v(x)2] = \(\left[\!v(x)\!\left(\!\mathop {\lim }\limits_{h \to 0} \frac{u(x+h) - u(x)}{h}\right)\!\!\!-\!\!u(x)\!\!\left( \mathop {\lim }\limits_{h \to 0} \!\!\frac{v(x + h) - v(x)}{h} \right)\!\!\right]\) [1/v(x)2]

= \(\frac{v(x)u'(x) - u(x)v'(x)}{[v(x)]^2}\)

Quotient Rule Formula Proof Using Implicit Differentiation

To prove the quotient rule formula using implicit differentiation formula, let us take a differentiable function f(x) = u(x)/v(x), so u(x) = f(x)⋅v(x). Using the product rule, we have, u'(x) = f'(x)⋅v(x) + f(x)v'(x). Solving for f'(x), we get,

f'(x) = \(\frac{u'(x) - f(x)v'(x)}{v(x)}\)

Substitute f(x),

⇒ f'(x) = \(\frac{u'(x) - \frac{u(x)}{v(x)}v'(x)}{v(x)}\)

= \(\frac{u'(x)v(x) - u(x)v'(x)}{[v(x)]^2}\)

Quotient Rule Formula Proof Using Chain Rule

We can derive the quotient rule formula in calculus using the chain rule formula. Let f(x) be a differentiable function such that f(x) = u(x)/v(x).

⇒ f(x) = u(x)v-1(x) Using the product rule, f'(x) = u'(x)v-1(x) + u(x)⋅\(\left(\frac{d}{dx}(v^{-1}(x)\right)\)

Applying the power rule to solve the derivative in the second term, we have, f'(x) = u'(x)v-1(x) + u(x)⋅(-1)(v(x)-2)v'(x)

f'(x) = \(\frac{u'(x)}{v(x)} - \frac{u(x)v'(x)}{v(x)^2}\)

f'(x) = \(\frac{d}{dx} \left[ \frac{u(x)}{v(x)} \right] \) = \(\frac{u'(x)v(x) - u(x)v'(x)}{v(x)^2}\)

How to Apply Quotient Rule in Differentiation?

In order to find the derivative of the function of the form f(x) = u(x)/v(x), both u(x) and v(x) should be differentiable functions. We can apply the following given steps to find the derivation of a differentiable function f(x) = u(x)/v(x) using the quotient rule.

• Step 1: Note down the values of u(x) and v(x).
• Step 2: Find the values of u'(x) and v'(x) and apply the quotient rule formula, given as: f'(x) = [u(x)/v(x)]' = [u'(x) × v(x) - u(x) × v'(x)]/[v(x)]2

Let us have a look at the following example given below to understand the quotient rule better.

Example: Find f'(x) for the following function f(x) using the quotient rule: f(x) = x2/(x+1).

Solution:

Here, f(x) = x2/(x + 1)

u(x) = x2

v(x) = (x + 1)

⇒u'(x) = 2x ⇒v'(x) = 1

⇒f'(x) = [v(x)u'(x) - u(x)v'(x)]/[v(x)]2 ⇒f'(x) = [(x+1)•2x - x2•1]/(x + 1)2 ⇒f'(x) = (2x2 + 2x - x2)/(x + 1)2 ⇒f'(x) = (x2 + 2x​​​​)/(x + 1)2

Answer: The derivative of x2/(x + 1) is (x2 + 2x​​​​)/(x + 1)2.

☛ Topics Related to Quotient Rule:

• Applications of Derivatives
• Calculus
• Differential Equation