Regular Polygon Calculator

Pentagon Shape n=5 A 5 sided polygon

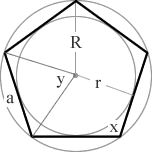
r = inradius (apothem) R = circumradius a = side length n = number of sides x = interior angle y = exterior angle A = area P = perimeter π = pi = 3.1415926535898 √ = square root

Polygon Calculator

Use this calculator to calculate properties of a regular polygon. Enter any 1 variable plus the number of sides or the polygon name. Calculates side length, inradius (apothem), circumradius, area and perimeter. Calculate from an regular 3-gon up to a regular 1000-gon.

Units: Note that units of length are shown for convenience. They do not affect the calculations. The units are in place to give an indication of the order of the calculated results such as ft, ft2 or ft3. Any other base unit can be substituted.

Regular Polygon Formulas

A regular polygon is a polygon that is both equiangular and equilateral. All sides are equal length placed around a common center so that all angles between sides are also equal. When the number of sides, n, is equal to 3 it is an equilateral triangle and when n = 4 is is a square.

The following formulas were used to develop calculations for this calculator where a = side length, r = inradius (apothem), R = circumradius, A = area, P = perimeter, x = interior angle, y = exterior angle and n = number of sides.

• Side Length a
  • a = 2r tan(π/n) = 2R sin(π/n)
• Inradius r
  • r = (1/2)a cot(π/n) = R cos(π/n)
• Circumradius R
  • R = (1/2) a csc(π/n) = r sec(π/n)
• Area A
  • A = (1/4)na2 cot(π/n) = nr2 tan(π/n)
• Perimeter P
  • P = na
• Interior Angle x
  • x = ((n-2)π / n) radians = (((n-2)/n) x 180° ) degrees
• Exterior Angle y
  • y = (2π / n) radians = (360° / n) degrees
  • 

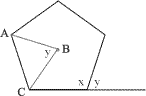
Selected Polygons

Polygon Name n Polygon Shape x y trigon (equilateral triangle) a 3 sided polygon 3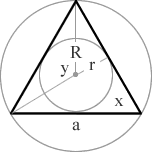 (1/3)π = 60° (2/3)π = 120° tetragon (square) a 4 sided polygon 4 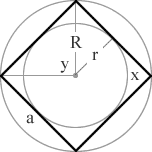(2/4)π = 90° (2/4)π = 90° pentagon a 5 sided polygon 5 (3/5)π = 108° (2/5)π = 72° hexagon a 6 sided polygon 6 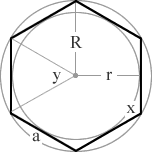(4/6)π = 120° (2/6)π = 60° heptagon a 7 sided polygon 7 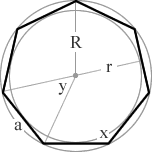(5/7)π = 900°/7 = 128.57° (2/7)π = 360°/7 = 51.43° octagon an 8 sided polygon 8 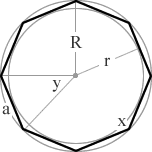(6/8)π = 135° (2/8)π = 45° nonagon a 9 sided polygon 9 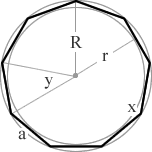(7/9)π = 140° (2/9)π = 40° decagon a 10 sided polygon 10 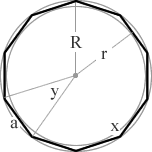(8/10)π = 144° (2/10)π = 36° undecagon an 11 sided polygon 11 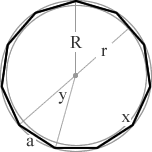(9/11)π = 1620°/11 = 147.27° (2/11)π = 360°/11 = 32.73° dodecagon a 12 sided polygon 12 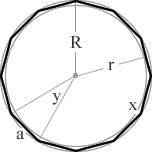(10/12)π = 150° (2/12)π = 30° tridecagon a 13 sided polygon 13 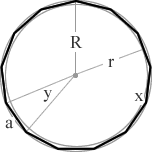(11/13)π = 1980°/13 = 152.31° (2/13)π = 360°/13 = 27.69° tetradecagon a 14 sided polygon 14 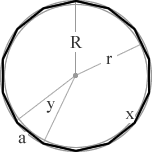(12/14)π = 2160°/14 = 154.29° (2/14)π = 360°/14 = 25.71°

References

Zwillinger, Daniel (Editor-in-Chief). CRC Standard Mathematical Tables and Formulae, 31st Edition New York, NY: CRC Press, p. 323, 2003.

Weisstein, Eric W. "Regular Polygon." From MathWorld--A Wolfram Web Resource. Regular Polygon.