Removable Discontinuity: Definition, Example & Graph - StudySmarter

Maybe your like

Learning Materials

Explanations Explanations
- Anthropology
- Archaeology
- Architecture
- Art and Design
- Bengali
- Biology
- Business Studies
- Chemistry
- Chinese
- Combined Science
- Computer Science
- Economics
- Engineering
- English
- English Literature
- Environmental Science
- French
- Geography
- German
- Greek
- History
- Hospitality and Tourism
- Human Geography
- Japanese
- Italian
- Law
- Macroeconomics
- Marketing
- Math
- Media Studies
- Medicine
- Microeconomics
- Music
- Nursing
- Nutrition and Food Science
- Physics
- Politics
- Polish
- Psychology
- Religious Studies
- Sociology
- Spanish
- Sports Sciences
- Translation

Features

Flashcards
StudySmarter AI
Notes
Study Plans
Study Sets
Exams

Discover

Find a job
Student Deals
Magazine
Mobile App

Explanations
Math
Calculus
Removable Discontinuity

Removable Discontinuity

A removable discontinuity is a point where a function does not exist, but if you move to this point from the left or right is the same.

Get started

Millions of flashcards designed to help you ace your studies

+ Add tag
Immunology
Cell Biology
Mo

What is StudySmarter?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

How does StudySmarter help me study more efficiently?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

Where can I find more explanations like this?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

What's smart about StudySmarter's flashcards?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

Can I create my own content on StudySmarter?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

How does spaced repetition work in StudySmarter flashcards?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

What can you do with flashcards in StudySmarter?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

Is StudySmarter a science-based learning platform?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

How do StudySmarter's smart learning plans support your exam prep?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

Can you create your own study sets in StudySmarter?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

What is StudySmarter?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

How does StudySmarter help me study more efficiently?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

Where can I find more explanations like this?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

What's smart about StudySmarter's flashcards?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

Can I create my own content on StudySmarter?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

How does spaced repetition work in StudySmarter flashcards?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

What can you do with flashcards in StudySmarter?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

Is StudySmarter a science-based learning platform?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

How do StudySmarter's smart learning plans support your exam prep?

Show Answer

+ Add tag
Immunology
Cell Biology
Mo

Can you create your own study sets in StudySmarter?

Show Answer Flashcards Icon

Generate flashcards Summarize Icon

Summarize page Flashcards Icon

Generate flashcards from highlight

Review generated flashcards

to start learning or create your own AI flashcards

Start learning or create your own AI flashcards

StudySmarter Editorial Team

Team Removable Discontinuity Teachers

7 minutes reading time
Checked by StudySmarter Editorial Team

Save Article Save Article Sign up for free to save, edit & create flashcards. Save Article Save Article

Fact Checked Content
Last Updated: 07.02.2023
Published at: 14.06.2022
7 min reading time

Applied Mathematics
Calculus

Absolute Maxima and Minima
Absolute and Conditional Convergence
Accumulation Function
Accumulation Problems
Algebraic Functions
Alternating Series
Antiderivatives
Application of Derivatives
Application of Higher Order Derivatives
Application of Integrals in Biology and Social Sciences
Applications of Continuity
Applications of Double Integrals
Approximating Areas
Arc Length of a Curve
Area Between Two Curves
Arithmetic Series
Arithmetic of Complex Numbers
Average Rate of Change of Populations
Average Value Function
Average Value of a Function
Bifurcation Theory
Boundary Value Problems
Calculus Linear Approximation
Calculus Of Parametric Curves
Candidate Test
Change of Variables in Multiple Integrals
Combining Different Rules
Combining Differentiation Rules
Combining Functions
Complex Analysis
Concavity of a Function
Continuity
Continuity Equations
Continuity Over an Interval
Continuity and Indeterminate Forms
Convergence Tests
Cost and Revenue
Critical points
Curl and Divergence
Curve Sketching Techniques
Density and Center of Mass
Derivative Functions
Derivative Properties
Derivative as a Limit
Derivative of Exponential Function
Derivative of Inverse Function
Derivative of Logarithmic Functions
Derivative of Trigonometric Functions
Derivative of Vector Valued Function
Derivatives
Derivatives and Continuity
Derivatives and the Shape of a Graph
Derivatives of Exponential Functions
Derivatives of Inverse Trigonometric Functions
Derivatives of Logarithmic Functions
Derivatives of Polar Functions
Derivatives of Sec, Csc and Cot
Derivatives of Sin, Cos and Tan
Determining Volumes by Slicing
Difference Quotient
Differentiability
Differentials
Differentiation of Functions of Several Variables
Direction Fields
Disk Method
Divergence Test
Double Integral
Double Integrals Over General Regions
Double Integrals Over Rectangular Regions
Double Integrals in Polar Coordinates
Dynamical Systems
Eliminating The Parameter
Euler's Method
Evaluating a Definite Integral
Evaluation Theorem
Exact equations
Exponential Functions
Exponential Model
Extrema
Finding Limits
Finding Limits of Specific Functions
First Derivative Test
Function Transformations
Fundamental Theorem of Line Integrals
Galois Theory
General Solution of Differential Equation
Geometric Series
Gradient Descent
Graphing and Optimization
Green's Function
Green's Theorem
Growth Rate of Functions
Harmonic Functions
Higher Order Partial Derivatives
Higher-Order Derivatives
Hydrostatic Pressure
Hyperbolic Functions
Implicit Differentiation Tangent Line
Implicit Relations
Improper Integrals
Increasing and Decreasing Functions
Indefinite Integral
Indeterminate Forms
Indeterminate Forms of Limits
Initial Value Problem Differential Equations
Integral Equations
Integral Test
Integrals in Economics
Integrals of Exponential Functions
Integrals of Motion
Integrating Even and Odd Functions
Integration Formula
Integration Tables
Integration Techniques
Integration Using Long Division
Integration Using Tables
Integration fundamentals
Integration of Logarithmic Functions
Integration of Vector Valued Functions
Integration using Inverse Trigonometric Functions
Intermediate Value Theorem
Inverse Trigonometric Functions
Jump Discontinuity
Lagrange Error Bound
Lagrange Multiplier
Laplace Transform
Lebesgue Integration
Limit Applications
Limit Laws
Limit of Vector Valued Function
Limit of a Sequence
Limits
Limits and Continuity
Limits at Infinity
Limits at Infinity and Asymptotes
Limits of a Function
Line Integrals
Linear Approximations and Differentials
Linear Differential Equation
Linear Functions
Logarithmic Differentiation
Logarithmic Functions
Logistic Differential Equation
Logistic Model
Maclaurin Series
Manipulating Functions
Matrix Theory
Maxima and Minima
Maxima and Minima Problems
Mean Value Theorem for Integrals
Measure Theory
Michaelis Menten Equation
Models for Population Growth
Motion Along A Line
Motion In Space
Multiple Integrals
Multivariable Calculus
Natural Logarithmic Function
Net Change Theorem
Newton's Method
Non Differentiable Functions
Nonhomogeneous Differential Equation
Nonlinear Differential Equations
Numerical Linear Algebra
One-Sided Limits
Optimization Problems
Optimization Problems in Economics
Optimization Theory
Ordinary Differential Equations
P Series
PDE Solutions
Parametric Surface Area
Parametric derivatives
Partial Derivatives
Particle Model Motion
Particular Solutions to Differential Equations
Piecewise Defined Function
Polar Coordinates
Polar Coordinates Functions
Polar Curves
Population Change
Power Series
Probability Theory
Properties of Definite Integrals
Radius of Convergence
Ratio Test
Real Analysis
Related Rates
Removable Discontinuity
Revenue as Average Rate of Change
Riemann Integral
Riemann Sum
Rolle's Theorem
Root Test
Second Derivative Test
Separable Equations
Separable differential equations
Separation of Variables
Simpson's Rule
Slope Fields
Solid of Revolution
Solutions to Differential Equations
Solving Inequalities using Continuity Properties
Spectral Theory
Stochastic Differential Equations
Surface Area Integral
Surface Area of Revolution
Surface Integrals
Surplus
Symmetry of Functions
Tangent Lines
Tangent Plane
Tangent Planes and Linear Approximations
Taylor Polynomials
Taylor Series
Techniques of Integration
The Fundamental Theorem of Calculus
The Limit Does Not Exist
The Mean Value Theorem
The Power Rule
The Squeeze Theorem
The Trapezoidal Rule
Theorems of Continuity
Topology
Trigonometric Substitution
Triple Integral
Triple Integral Spherical Coordinates
Triple Integrals in Cylindrical Coordinates
Types of Discontinuity
Using Slope Fields to Graph Solutions
Variational Methods
Vector Valued Function
Vectors In Space
Vectors in Calculus
Velocity as Average Rate of Change
Vertical Asymptote
Volume Integrals
Volume by disks
Volume by shells
Washer Method

Decision Maths
Discrete Mathematics
Geometry
Logic and Functions
Mechanics Maths
Probability and Statistics
Pure Maths
Statistics
Theoretical and Mathematical Physics

Contents

Applied Mathematics
Calculus

Absolute Maxima and Minima
Absolute and Conditional Convergence
Accumulation Function
Accumulation Problems
Algebraic Functions
Alternating Series
Antiderivatives
Application of Derivatives
Application of Higher Order Derivatives
Application of Integrals in Biology and Social Sciences
Applications of Continuity
Applications of Double Integrals
Approximating Areas
Arc Length of a Curve
Area Between Two Curves
Arithmetic Series
Arithmetic of Complex Numbers
Average Rate of Change of Populations
Average Value Function
Average Value of a Function
Bifurcation Theory
Boundary Value Problems
Calculus Linear Approximation
Calculus Of Parametric Curves
Candidate Test
Change of Variables in Multiple Integrals
Combining Different Rules
Combining Differentiation Rules
Combining Functions
Complex Analysis
Concavity of a Function
Continuity
Continuity Equations
Continuity Over an Interval
Continuity and Indeterminate Forms
Convergence Tests
Cost and Revenue
Critical points
Curl and Divergence
Curve Sketching Techniques
Density and Center of Mass
Derivative Functions
Derivative Properties
Derivative as a Limit
Derivative of Exponential Function
Derivative of Inverse Function
Derivative of Logarithmic Functions
Derivative of Trigonometric Functions
Derivative of Vector Valued Function
Derivatives
Derivatives and Continuity
Derivatives and the Shape of a Graph
Derivatives of Exponential Functions
Derivatives of Inverse Trigonometric Functions
Derivatives of Logarithmic Functions
Derivatives of Polar Functions
Derivatives of Sec, Csc and Cot
Derivatives of Sin, Cos and Tan
Determining Volumes by Slicing
Difference Quotient
Differentiability
Differentials
Differentiation of Functions of Several Variables
Direction Fields
Disk Method
Divergence Test
Double Integral
Double Integrals Over General Regions
Double Integrals Over Rectangular Regions
Double Integrals in Polar Coordinates
Dynamical Systems
Eliminating The Parameter
Euler's Method
Evaluating a Definite Integral
Evaluation Theorem
Exact equations
Exponential Functions
Exponential Model
Extrema
Finding Limits
Finding Limits of Specific Functions
First Derivative Test
Function Transformations
Fundamental Theorem of Line Integrals
Galois Theory
General Solution of Differential Equation
Geometric Series
Gradient Descent
Graphing and Optimization
Green's Function
Green's Theorem
Growth Rate of Functions
Harmonic Functions
Higher Order Partial Derivatives
Higher-Order Derivatives
Hydrostatic Pressure
Hyperbolic Functions
Implicit Differentiation Tangent Line
Implicit Relations
Improper Integrals
Increasing and Decreasing Functions
Indefinite Integral
Indeterminate Forms
Indeterminate Forms of Limits
Initial Value Problem Differential Equations
Integral Equations
Integral Test
Integrals in Economics
Integrals of Exponential Functions
Integrals of Motion
Integrating Even and Odd Functions
Integration Formula
Integration Tables
Integration Techniques
Integration Using Long Division
Integration Using Tables
Integration fundamentals
Integration of Logarithmic Functions
Integration of Vector Valued Functions
Integration using Inverse Trigonometric Functions
Intermediate Value Theorem
Inverse Trigonometric Functions
Jump Discontinuity
Lagrange Error Bound
Lagrange Multiplier
Laplace Transform
Lebesgue Integration
Limit Applications
Limit Laws
Limit of Vector Valued Function
Limit of a Sequence
Limits
Limits and Continuity
Limits at Infinity
Limits at Infinity and Asymptotes
Limits of a Function
Line Integrals
Linear Approximations and Differentials
Linear Differential Equation
Linear Functions
Logarithmic Differentiation
Logarithmic Functions
Logistic Differential Equation
Logistic Model
Maclaurin Series
Manipulating Functions
Matrix Theory
Maxima and Minima
Maxima and Minima Problems
Mean Value Theorem for Integrals
Measure Theory
Michaelis Menten Equation
Models for Population Growth
Motion Along A Line
Motion In Space
Multiple Integrals
Multivariable Calculus
Natural Logarithmic Function
Net Change Theorem
Newton's Method
Non Differentiable Functions
Nonhomogeneous Differential Equation
Nonlinear Differential Equations
Numerical Linear Algebra
One-Sided Limits
Optimization Problems
Optimization Problems in Economics
Optimization Theory
Ordinary Differential Equations
P Series
PDE Solutions
Parametric Surface Area
Parametric derivatives
Partial Derivatives
Particle Model Motion
Particular Solutions to Differential Equations
Piecewise Defined Function
Polar Coordinates
Polar Coordinates Functions
Polar Curves
Population Change
Power Series
Probability Theory
Properties of Definite Integrals
Radius of Convergence
Ratio Test
Real Analysis
Related Rates
Removable Discontinuity
Revenue as Average Rate of Change
Riemann Integral
Riemann Sum
Rolle's Theorem
Root Test
Second Derivative Test
Separable Equations
Separable differential equations
Separation of Variables
Simpson's Rule
Slope Fields
Solid of Revolution
Solutions to Differential Equations
Solving Inequalities using Continuity Properties
Spectral Theory
Stochastic Differential Equations
Surface Area Integral
Surface Area of Revolution
Surface Integrals
Surplus
Symmetry of Functions
Tangent Lines
Tangent Plane
Tangent Planes and Linear Approximations
Taylor Polynomials
Taylor Series
Techniques of Integration
The Fundamental Theorem of Calculus
The Limit Does Not Exist
The Mean Value Theorem
The Power Rule
The Squeeze Theorem
The Trapezoidal Rule
Theorems of Continuity
Topology
Trigonometric Substitution
Triple Integral
Triple Integral Spherical Coordinates
Triple Integrals in Cylindrical Coordinates
Types of Discontinuity
Using Slope Fields to Graph Solutions
Variational Methods
Vector Valued Function
Vectors In Space
Vectors in Calculus
Velocity as Average Rate of Change
Vertical Asymptote
Volume Integrals
Volume by disks
Volume by shells
Washer Method

Decision Maths
Discrete Mathematics
Geometry
Logic and Functions
Mechanics Maths
Probability and Statistics
Pure Maths
Statistics
Theoretical and Mathematical Physics

Contents

Fact Checked Content
Last Updated: 07.02.2023
7 min reading time

Content creation process designed by Lily Hulatt
Content sources cross-checked by Gabriel Freitas
Content quality checked by Gabriel Freitas

Jump to a key chapter

In the Continuity article, we learned three criteria needed for a function to be continuous. Recall that all three of these criteria must be met for continuity at a point. Let's consider the third criterion for a minute "the limit as x approaches a point must be equal to the function value at that point". What if, say, this is not met (but the limit still exists)? What would that look like? We call it a removable discontinuity (also known as a hole)! Let's take a further look.

Removable Point of Discontinuity

Let's go back to the scenario in the introduction. What happens if the limit exists, but isn't equal to the function value? Recall, that by saying the limit exists what you actually are saying is that it is a number, not infinity.

If a function \(f(x)\) is not continuous at \(x=p\), and

\[lim_{x \rightarrow p} f(x)\]

exists, then we say the function has a removable discontinuity at \(x=p\).

Here, we define \(x=p\) as a removable point of discontinuity.

Ok, that's great, but what does a removable discontinuity look like? Consider the image below.

Removable discontinuity example graph StudySmarter Fig. 1. Example of a function with a removable discontinuity at \(x = p\).

In this image, the graph has a removable discontinuity (aka. a hole) in it and the function value at \(x=p\) is \(4\) instead of the \(2\) you would need it to be if you wanted the function to be continuous. If instead that hole were filled in with the point above it, and the point floating there removed, the function would become continuous at \(x=p\). This is called a removable discontinuity.

Removable Discontinuity Example

Let's take a look at a few functions and determine if they have removable discontinuities.

Removable Discontinuity Graph

Does the function \(f(x)=\dfrac{x^2-9}{x-3}\) have a removable discontinuity at \(x=3\) ?

Answer:

First, notice that the function isn't defined at \(x=3\), so it isn't continuous there. If the function is continuous at \(x=3\), then it certainly doesn't have a removable discontinuity there! So now you need to check the limit:

\[lim_{x \rightarrow 3} f(x)\]

Since the limit of the function does exist, the discontinuity at \(x=3\) is a removable discontinuity. Graphing the function gives:

Fig, 1. This function has a hole at \(x=3\) because the limit exists, however, \(f(3)\) does not exist.

Removable discontinuity example graph StudySmarter Fig. 2. Example of a function with a removable discontinuity at \(x = 3\).

So you can see there is a hole in the graph.

Non-removable Discontinuities

If some discontinuities can be removed, what does it mean to be non-removable? Looking at the definition of a removable discontinuity, the part that can go wrong is the limit not existing. Non-removable discontinuities refer to two other main types of discontinues; jump discontinuities and infinite/asymptotic discontinuities. You can learn more about them in Jump Discontinuity and Continuity Over an Interval.

Non-removable Discontinuity Graph

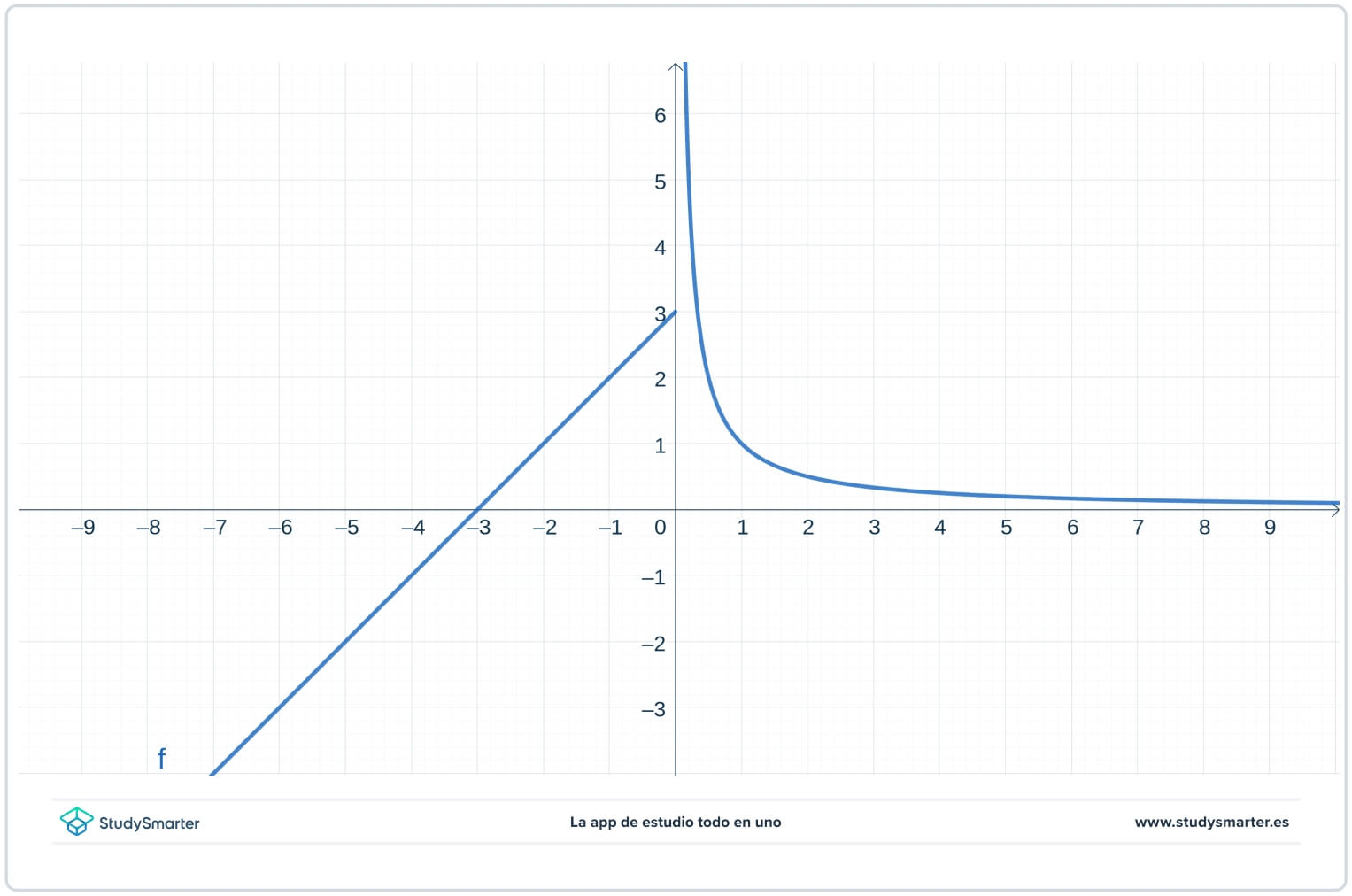
Looking at the graph of the piecewise-defined function below, does it have a removable or non-removable point of discontinuity at \(x=0\)? If it is non-removable, is it an infinite discontinuity?

Removable discontinuity example infinite discontinuity StudySmarter

Fig. 3. Function with a non-removable discontinuity.

Answer:

From looking at the graph you can see that

\[lim_{x \rightarrow 0^-}f(x)=3\]

and that

\[lim_{x \rightarrow 0^+}f(x)=\infty\]

which means the function is not continuous at \(x=0\). In fact, it has a vertical asymptote at \(x=0\). Since those two limits aren't the same number, the function has a non-removable discontinuity at \(x=0\). Since one of those limits is infinite, you know it has an infinite discontinuity at \(x=0\).

Deciding if the function has a removable or non-removable point of discontinuity

Removable Discontinuity Limit

How can you tell if the discontinuity of a function is removable or non-removable? Just look at the limit!

If the limit from the left at \(p\) and the right at \(p\) are the same number, but that isn't the value of the function at \(p\) or the function doesn't have a value at \(p\), then there is a removable discontinuity.
If the limit from the left at \(p\), or the limit from the right at \(p\), is infinite, then there is a non-removable point of discontinuity, and it is called an infinite discontinuity.

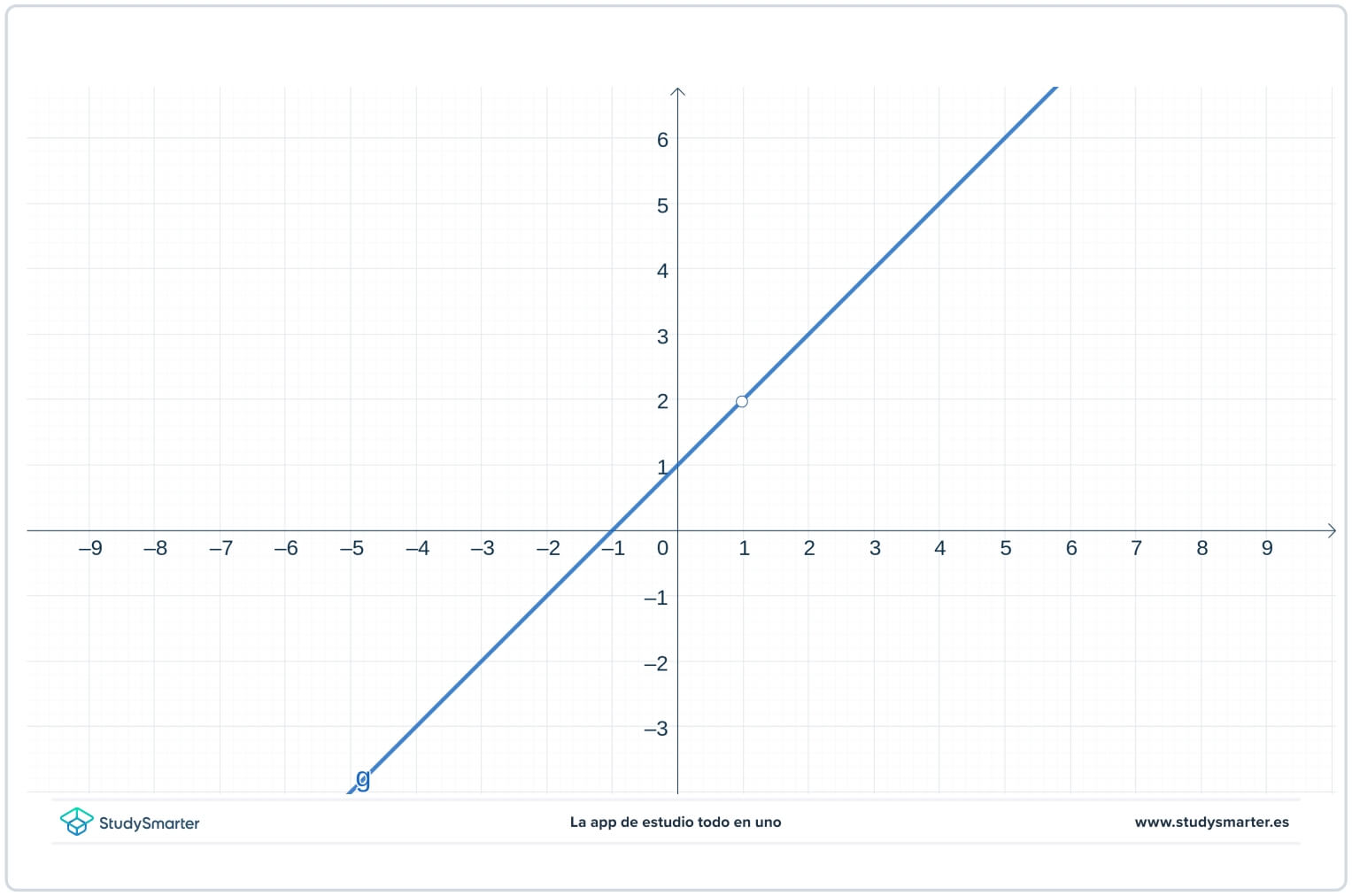
What kind of discontinuity, if any, does the function in the graph have at \(p\)?

Removable discontinuity example graph StudySmarter

Fig. 4. This function has a removable discontinuity at \(x=p\) because the limit is defined, however,\( f(p)\) does not exist.

Answer:

You can see looking at the graph that the function isn't even defined at \(p\). However the limit from the left at \(p\) and the limit from the right at \(p\) are the same, so the function has a removable point of discontinuity at \(p\). Intuitively, it has a removable discontinuity because if you just filled in the hole in the graph, the function would be continuous at \(p\). In other words, removing the discontinuity means changing just one point on the graph.

What kind of discontinuity, if any, does the function in the graph have at \(p\)?

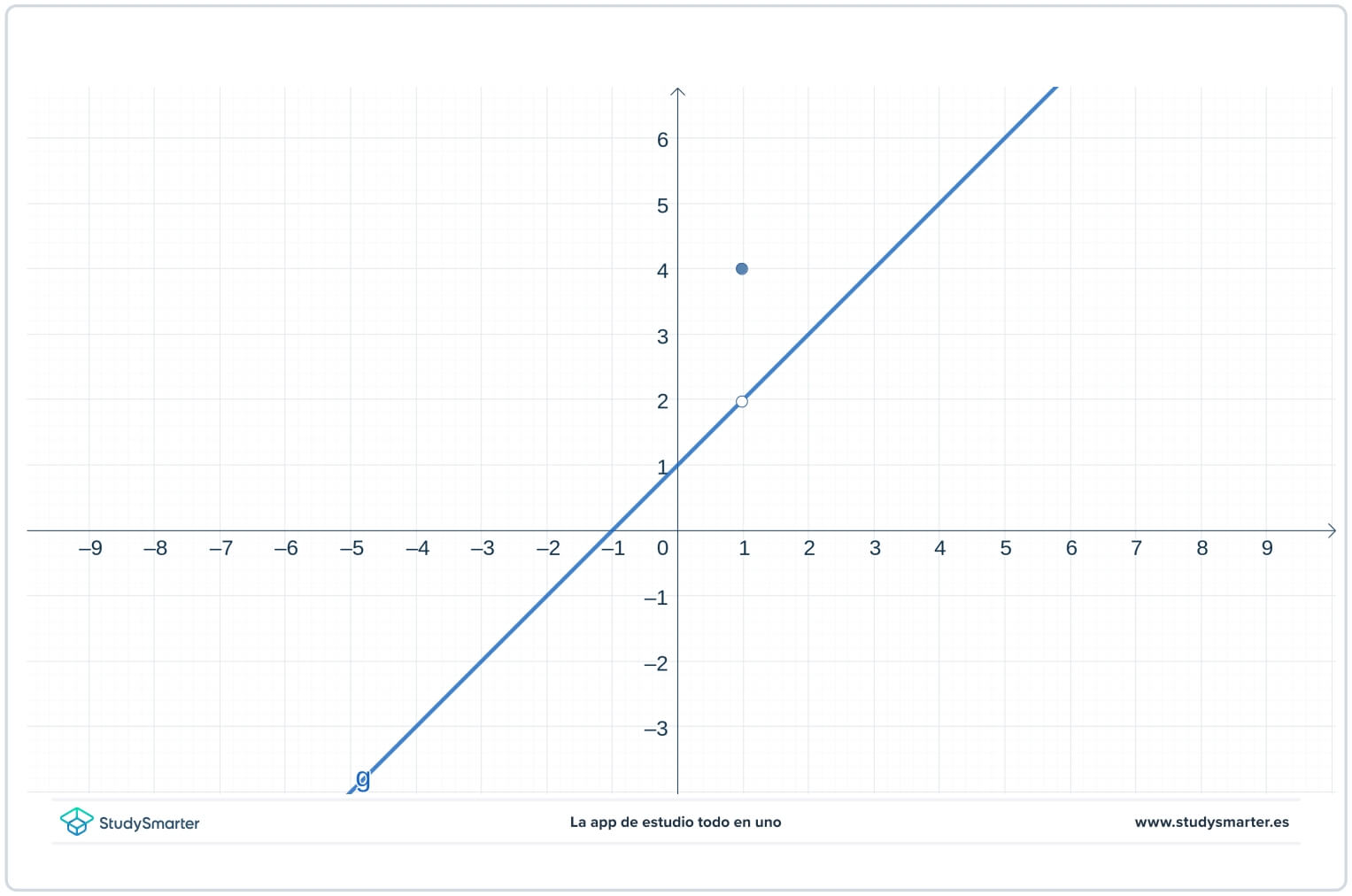
Removable discontinuity example graph StudySmarter

Fig. 5. This function is defined everywhere.

Unlike in the previous example, you can see looking at the graph that the function is defined at \(p\). However the limit from the left at \(p\) and the limit from the right at \(p\) are the same, so the function has a removable point of discontinuity at \(p\). Intuitively, it has a removable discontinuity because if you just changed the function so that rather than having it filled in the hole, the function would be continuous at \(p\).

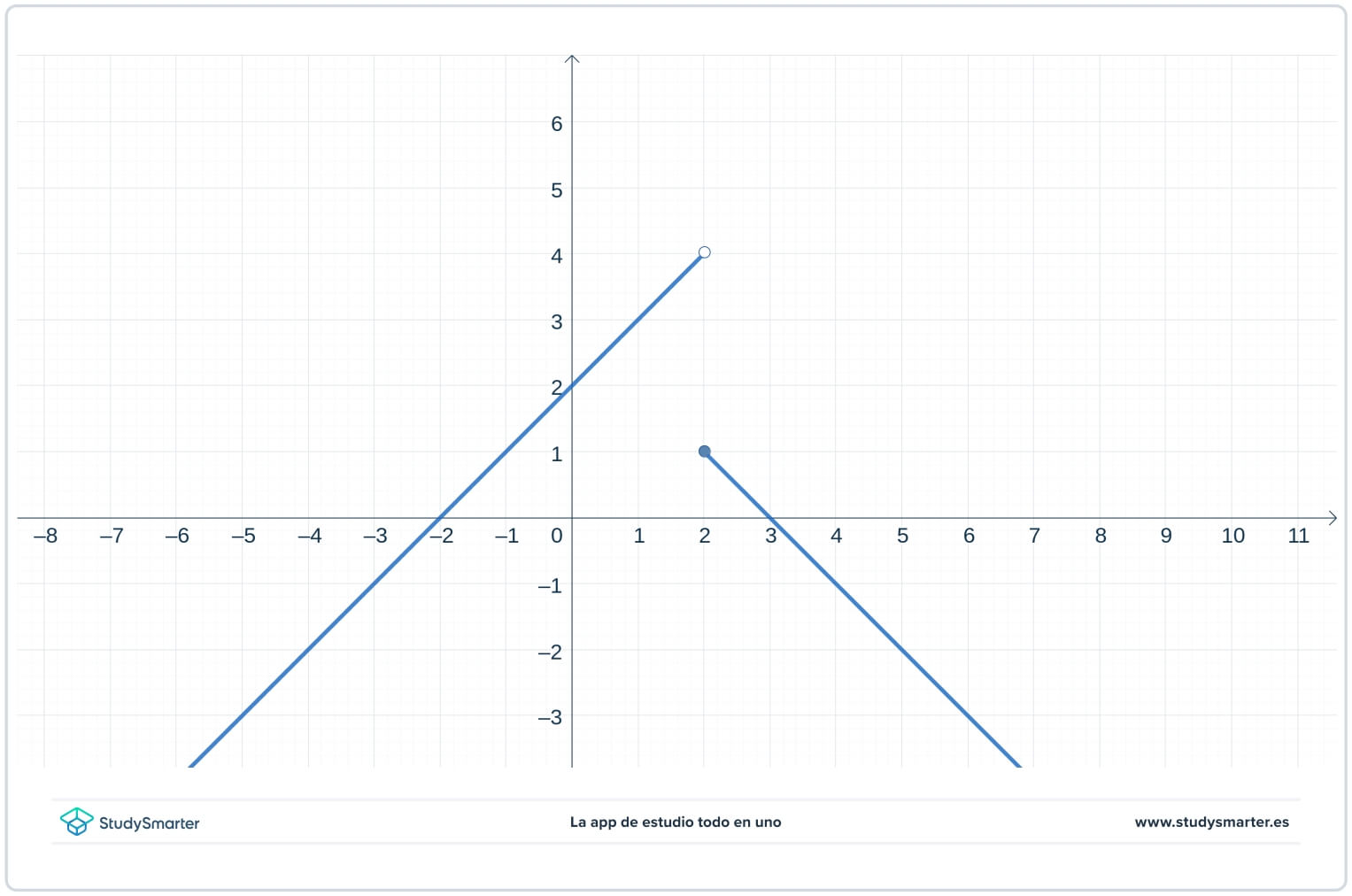
Looking at the graph of the piecewise-defined function below, does it have a removable, non-removable discontinuity, or neither of the two?

Removable Discontinuity graph non-removable jump StudySmarter

Fig. 6. Graph of a function with a discontinuity at \(x=2\), StudySmarter Original.

Answer:

This function is clearly not continuous at \(2\) because the limit from the left at \(2\) is not the same as the limit from the right at \(2\). In fact

\[lim_{x \rightarrow 2^-}f(x)=4\]

and

\[lim_{x \rightarrow 2^+}f(x)=1\] .

So we know that

the limit from the left at \(2\) and the limit from the right of \(2\) don't have the same value
the limit from the left isn't infinite, and the limit from the right isn't infinite at \(2\) either,

Therefore, this function has a non-removable discontinuity at \(2\), however, it is not an infinite discontinuity.

In the example above, the function has a jump discontinuity at \(x=2\). For more information on when this happens, see Jump Discontinuity

Looking at the graph below, does the function have a removable or non-removable point of discontinuity at \(x=2\)?

Removable Discontinuity infinite type graph StudySmarter

Fig. 7. Graph of a function with a discontinuity at \(x = 2\).

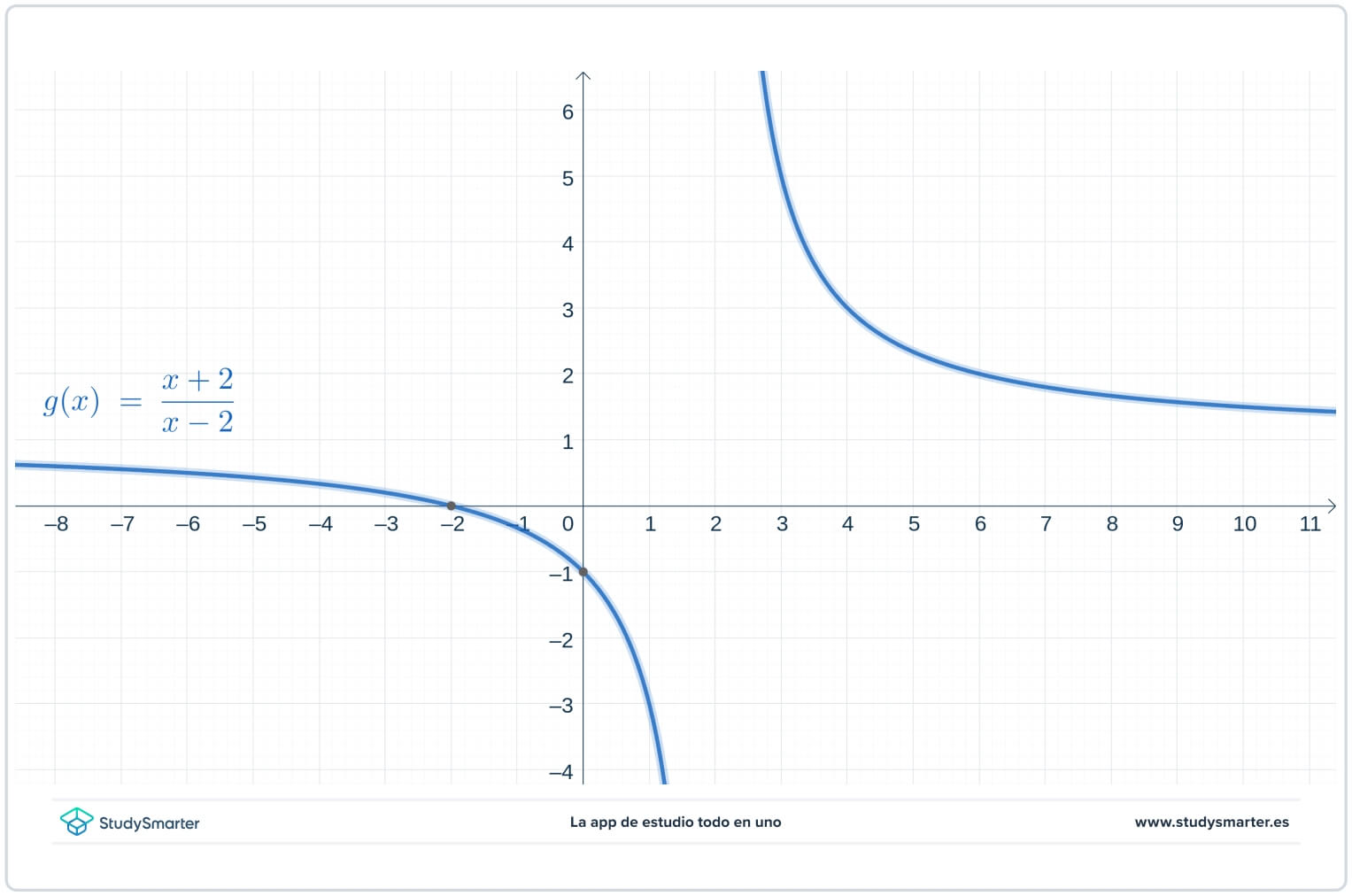
Answer:

This function has a vertical asymptote at \(x=2\). In fact

\[lim_{x \rightarrow 2^-}f(x)= -\infty\]

and

\[lim_{x \rightarrow 2^+}f(x)= \infty\]

So this function has a non-removable point of discontinuity. It is called an infinite discontinuity because one of the limits is infinite.

Removable Discontinuity - Key takeaways

If a function is not continuous at a point, we say "it has a point of discontinuity at this point".
If a function is not continuous at a point, then we say the function has a removable discontinuity at this point if the limit at this point exists.
If the function has a removable discontinuity at a point, then is called a removable point of discontinuity (or a hole).

Learn faster with the 0 flashcards about Removable Discontinuity

Already have an account? Log in

Frequently Asked Questions about Removable Discontinuity

What is the difference between removable and nonremovable discontinuity?

For a discontinuity at x=p to be removable the limit from the left and the limit from the right at x=p have to be the same number. If one of them (or both) is infinite, then the discontinuity is non-removable.

What is a removable discontinuity?

A removable discontinuity happens when a function is not continuous at x = p, but the limit from the left and the limit from the right at x = p exist and have the same value.

How to find a removable discontinuity

Look for a place in the function where the limit from the left and right are the same number but that isn't the same as the function value there.

Which functions have removable discontinuities?

There are lots of functions with removable discontinuities. Just look for a hole in the graph.

How do you know if a discontinuity is removable?

If the limit of the function f(x) exists at x=p. but isn't equal to f(p), then you know it has a removable discontinuity.

Save Article

How we ensure our content is accurate and trustworthy?

At StudySmarter, we have created a learning platform that serves millions of students. Meet the people who work hard to deliver fact based content as well as making sure it is verified.

Content Creation Process: Lily Hulatt Avatar

Lily Hulatt

Digital Content Specialist

Lily Hulatt is a Digital Content Specialist with over three years of experience in content strategy and curriculum design. She gained her PhD in English Literature from Durham University in 2022, taught in Durham University’s English Studies Department, and has contributed to a number of publications. Lily specialises in English Literature, English Language, History, and Philosophy.

Get to know Lily Content Quality Monitored by: Gabriel Freitas Avatar

Gabriel Freitas

AI Engineer

Gabriel Freitas is an AI Engineer with a solid experience in software development, machine learning algorithms, and generative AI, including large language models’ (LLMs) applications. Graduated in Electrical Engineering at the University of São Paulo, he is currently pursuing an MSc in Computer Engineering at the University of Campinas, specializing in machine learning topics. Gabriel has a strong background in software engineering and has worked on projects involving computer vision, embedded AI, and LLM applications.

Get to know Gabriel Discover learning materials with the free StudySmarter app Sign up for free

About StudySmarter

StudySmarter is a globally recognized educational technology company, offering a holistic learning platform designed for students of all ages and educational levels. Our platform provides learning support for a wide range of subjects, including STEM, Social Sciences, and Languages and also helps students to successfully master various tests and exams worldwide, such as GCSE, A Level, SAT, ACT, Abitur, and more. We offer an extensive library of learning materials, including interactive flashcards, comprehensive textbook solutions, and detailed explanations. The cutting-edge technology and tools we provide help students create their own learning materials. StudySmarter’s content is not only expert-verified but also regularly updated to ensure accuracy and relevance.

Learn more

StudySmarter Editorial Team

Team Math Teachers

7 minutes reading time
Checked by StudySmarter Editorial Team

Save Explanation Save Explanation Study anywhere. Anytime.Across all devices. Sign-up for free Create a free account to save this explanation.

Save explanations to your personalised space and access them anytime, anywhere!

By signing up, you agree to the Terms and Conditions and the Privacy Policy of StudySmarter.

Already have an account? Log in

Get Started Free Explore our app and discover over 50 million learning materials for free. Sign up for free 94% of StudySmarter users achieve better grades with our free platform. Download now!

Tag » What Is A Removable Discontinuity

Removable Discontinuity: Definition, Example & Graph - StudySmarter

Removable Point of Discontinuity

Removable Discontinuity Example

Removable Discontinuity Graph

Non-removable Discontinuities

Non-removable Discontinuity Graph

Deciding if the function has a removable or non-removable point of discontinuity

Removable Discontinuity Limit

Removable Discontinuity - Key takeaways

Similar topics in Math

Related topics to Calculus

Learn faster with the 0 flashcards about Removable Discontinuity

Frequently Asked Questions about Removable Discontinuity

How we ensure our content is accurate and trustworthy?

About StudySmarter

What Is Removable Discontinuity Class 11 Maths CBSE - Vedantu

Non Removable And Jump Discontinuity - Cuemath

What Is Removable Discontinuity? - Education Is Around

Removable Discontinuity -- From Wolfram MathWorld

Removable Discontinuities: Definition & Concept

How To Find REMOVABLE DISCONTINUITIES (KristaKingMath)

Types Of Discontinuities (video) - Khan Academy

Removable Discontinuity - Superprof

Removable Discontinuity - Mathwords

Classification Of Discontinuities - Wikipedia

What Is Removable Discontinuity? How Do You Identify Functions ...

Continuity And Discontinuity | CK-12 Foundation

How To Determine Whether A Function Is Discontinuous - Dummies

Contact