SAS Triangle – Formula, Theorem, Solved Examples - Math Monks

What are SAS Triangles

SAS means ‘Angle-Side-Angle’. SAS triangles are triangles where two sides and the angle between them are known. Shown below is a SAS triangle, △ABC, where b and c are the two known sides, while ∠B is the known, common angle present between the two sides.

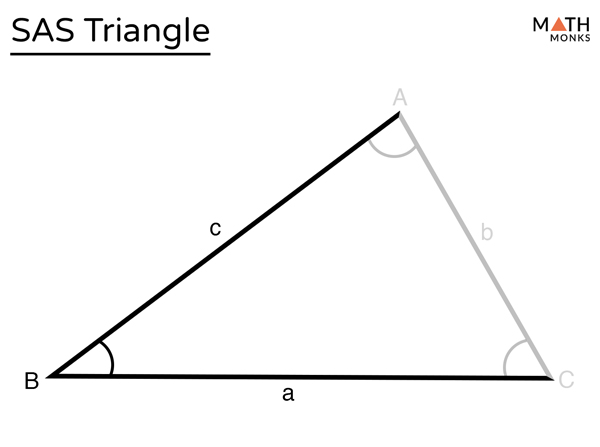
How to Solve SAS Triangle

It involves three steps:

Step 1: Use the Law of Cosines to calculate the missing side

Step 2: Use The Law of Sines to find the smaller of the two unknown angles

Step 3: Use the angle sum rule of a triangle to find the last angle

Let us take some examples to understand the concept better.

Solved Examples

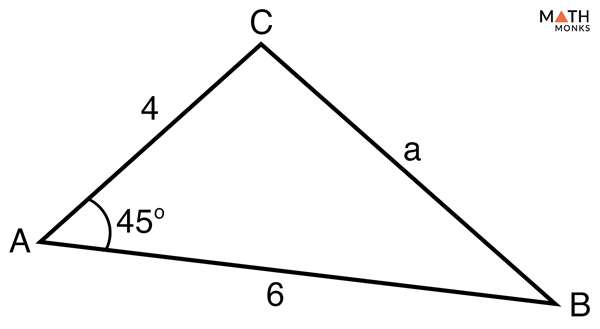Find the missing angles and the side in the given SAS triangle.

Solution:

In the triangle, the given angles and side is:Side b = 4Side c = 6∠A = 45°Step 1:Using theLaw of Cosines, we will calculate the missing side, side aa2 = b2 + c2 − 2bc cos A, here b = 4, c = 6, ∠A = 45°a2 = 42 + 62 – 2 x 4 x 6 x cos 45°a2 = 16 + 36 – 48 x cos 45°a2 = 52 – 48 x 0.70a2 = 52 – 33.6a2 = 18.4a = 4.28Step 2:Now, we use The Law of Sines to find the smaller of the two unknown anglesWhy the Smaller Angle to be Determined First?The smaller angle is determined first because the inverse sine function gives answers less than 90° even for angles greater than 90°. By choosing the smaller angle a triangle cannot have two angles greater than 90°.a/sin A = b/sin B, here ∠A = 45°, a = 4.28, b = 44.28/sin 45° = 4/sin Bsin B = 4 x sin 45°/4.28sin B = 4 x 0.70/4.28sin B = 0.65B = sin -1 (0.65)B = 40.54°Step 3:Finally, we will use the angle sum rule of a triangle to find the last undetermined angle, ∠C∠A + ∠B + ∠C = 180°, here ∠A = 45°, ∠B = 40.54°45° + 40.54° +∠C = 180°∠C = 180° – (45° + 40.54°)∠C = 94.46°

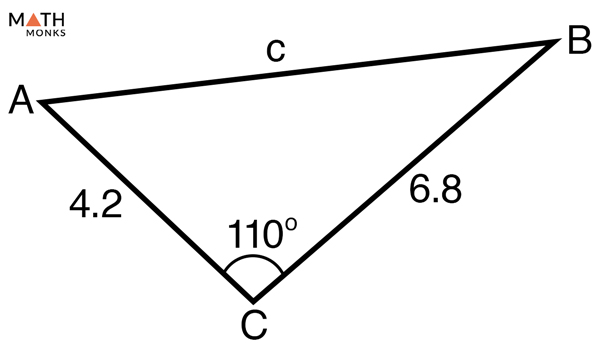Find the missing angles and the side in the given triangle.

Solution:

The given triangle is an SAS triangle.Here,Side a = 6.8Side b = 4.2∠C = 110°Step 1:Using theLaw of Cosines, we will calculate the missing side, side cc2 = a2 + b2 − 2ab cos C, here a = 6.8, b = 4.2, ∠C = 110°c2 = 6.82 + 4.22 – 2 x 6.8 x 4.2 x cos 110°c2 = 46.24 + 17.64 – 57.12 x (-0.34)c2 = 63.88 + 19.42c2 = 83.3c = 9.12Step 2:Now, for calculating the Law of Sines, we don’t need to look for the smaller angle as ∠C is greater than 90°, so ∠A and ∠B must be less than 90°.a/sin A = c/sin C, here, a = 6.8, c = 9.12, ∠C = 110°6.8/sin A = 9.12/ sin 110°sin A = 6.8 x sin 110°/9.12sin A = 6.8 x 0.93/9.12sin A = 0.69A = sin-1 (0.69)∠A = 43.63°Step 3:Finally, we will use the angle sum rule of a triangle to find the last undetermined angle, ∠B∠A + ∠B + ∠C = 180°, here ∠A = 43.63°, ∠C = 110°43.63° + ∠B + 110° = 180°∠B = 180° – (43.63° + 110°)∠B = 26.37°

SAS Triangle Congruence Theorem

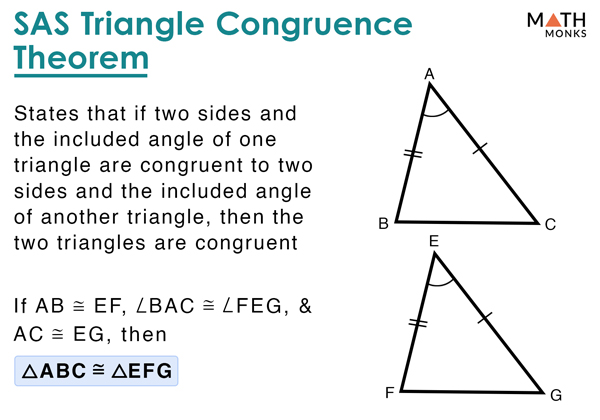
Let us take an example to understand the concept.

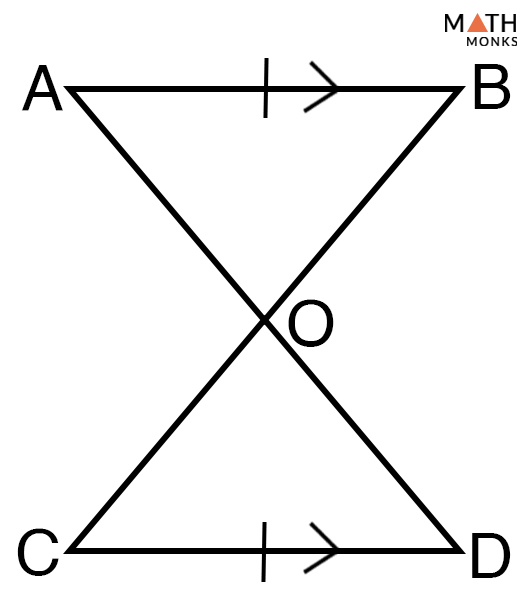
Proving Triangles Congruent using the Side-Angle-Side Theorem

To prove: ΔABO ≅ ΔCDO

Proof:

Steps	Statements	Reasons
1.	AB ≅ CD AB || CD	Given
2.	∠BAO ≅∠DCO	Alternate interior angles
3.	∠ABO ≅∠CDO	Alternate interior angles
4.	ΔABO ≅ ΔCDO	SAS postulate (Hence proved)

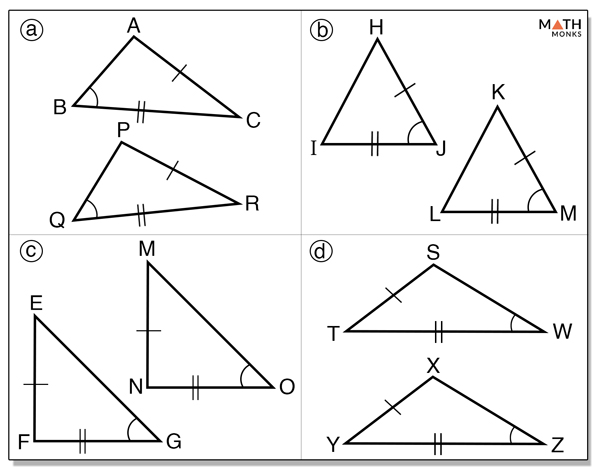Identify which pair of triangles below illustrates an SAS relationship to prove the triangles are congruent.

Solution:

Option (b). Here the triangles ΔHIJ and ΔKLM are congruent by the SAS relationship.

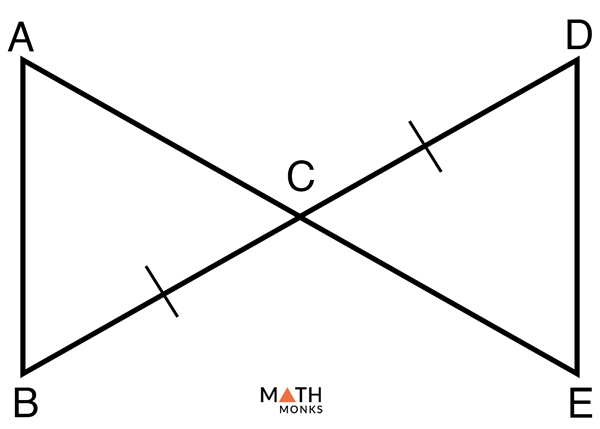Prove whether ΔABC and ΔDEC are congruent by SAS. Given that, BC ≅ DC and C is the midpoint of AE.

Solution:

Given that BC ≅ DC and C is the midpoint of AENow, according to the ‘Vertical Angles Theorem‘ ∠ACB ≅∠ECDAgain, AC ≅ EC as the midpoint C bisects AE into two congruent parts AC and ECHence ΔABC ≅ ΔDEC by SAS postulate (Proved)

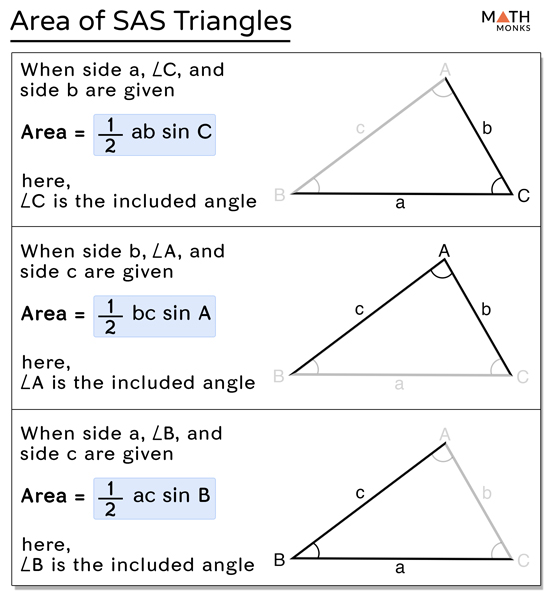
Area of a SAS Triangle

If ΔABC is an SAS triangle with side lengths a, b and c, then we can find its area with one of the three formulas given below:

How It Works

The method discussed above is just an extension of the general formula for determining the area of a triangle.

As we know, the general formula of area of a triangle is given by,

Area (A) = ½ x a x h, here a = base, h = height

But, if we are not given the height but we are given side b and angle C in the right triangle, ΔCDA

Using trigonometry, we can write

sin C = h/b

=> h = b sin C

Substituting the value of h in the general formula of area of a triangle, we get,

Area (A) = ½ x a x b sin C = ½ ab sin C

Let us solve an example using the above formula.

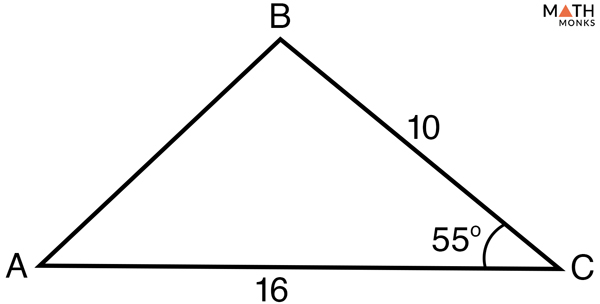Find the area of the given triangle.

Solution:

As the given triangle is an SAS triangle, we will use the formulaArea (A) = ½ ab sin C, here a = 10, b = 16, ∠C = 55° = ½ 10 x 16 sin 55°= 64.8 square units