Shape Selection And Mis-assembly In Viral Capsid Formation ... - ELife
Maybe your like
In the limit γ=YR02/κ≪1, the bending energy dominates over the stretching energy and thus, all structures will adopt their spontaneous curvature, R=R0. The situation will be similar to the growth of a crystal on a template of fixed curvature. In the bending-dominated regime, the free energy of formation of all these structures, when properly scaled by the characteristic elastic energy 4πR02Y, only depends on two parameters: the scaled chemical potential Δμ~≡Δμ/(Ya1) and the scaled line tension λ≡Λ/(R0Y). Thus, it is possible to compare them and determine the most stable structure for a given set of conditions. The comparison is performed for different shapes having the same area S , that is having the same number of subunits.
The scaled free energy of formation of a hexagonally-ordered spherical cap of radius R0 without defects made of a circular patch of radius ρ0 (see Figure 1a) is
(2) Δgcap=-Δμ~4x2+λ2x+11536x6where x≡ρ0/R0 is the scaled patch size, and the third term is the in-plane elastic energy of a circular domain on a curved spherical surface (Schneider and Gompper, 2007; Meng et al., 2014; Morozov and Bruinsma, 2010). (Equation 2 is an approximation strictly valid for small circular patches with an aperture angle θ≪π, since it is assumed that the perimeter of the shell is approximately the same as that of a circular disk, and a flat metric has been used to compute the in-plane elastic energy. However, we have found that a more accurate evaluation of the second and third terms in this equation [Li et al., 2018] does not alter significantly the main results.)
The stretching energy stored in the spherical shell grows fast with the area of the patch, and can be partially released by two different mechanisms: by the introduction of pentagonal defects (see Figure 1b), or by growing anisotropically forming curved ribbon-like crystalline domains (see Figure 1c).
The free energy of formation for a spherical cap with one defect is (Morozov and Bruinsma, 2010; Castelnovo, 2017)
(3) Δgd1=Δgcap+x21152(1-32x2),where the last term is the stretching energy due to a pentagonal disclination at the center of the cap. (The energy of an incomplete cap with one defect placed at an arbitrary location is calculated in Li et al., 2018. It is found that the Gaussian curvature attracts the disclination to the center of the cap while the defect self-energy pushes it towards the boundary. The net result is that the minimum energy corresponds to the defect located off the center of the cap. However, we have numerically verified that this approximation introduces only a very small error in our calculations for the scaled energy. This means that not noticeable effect is observed when the exact expression with the off-center defect is considered.) Such mechanism is energetically favorable only if the second term of Equation 3 is negative, that is, if x≥2/3.
For larger shells, the elastic strain is further released by the introduction of additional disclinations. The free energy of formation of a spherical shell with n 5-fold disclinations is (Grason, 2012; Grason, 2016; Castelnovo, 2017)
(4) Δgdn=Δgcap+gs1+gs2where gs1 is the self-energy of the isolated disclinations, and gs2 is their pairwise interaction, whose specific expressions are provided in the Appendix. When more than one defect appears, the minimum of the free energy typically occurs for a closed shell.
An alternative mechanism to alleviate stretching is the anisotropic growth of the originally spherical cap to adopt the shape of a defect-free rectangular curved stripe or ribbon. The free energy of formation of a ribbon of scaled length l≡L/R0, width w≡W/R0, and area s=lw=πx2 growing on the surface of a sphere of radius R0 is (Schneider and Gompper, 2007; Majidi and Fearing, 2008)
(5) Δgrib=-Δμ~4x2+λ2x2w+λ2πw+920480x2w4.Unlike the spherical cap, as the area of the patch increases, the ribbon grows longitudinally without limitation at a nearly fixed optimal width up to the point where l=2π, where it forms a closed belt with energy
(6) Δgbelt=-Δμ~4x2+λ+9327680x10.The ribbon-like structure with the lowest energy is always a closed belt rather than the open ribbon, so we will focus our comparison with this structure.
Finally, an alternative to the curved belt could be a cylinder with one principal radius of curvature infinitely large and the other R0 (see Figure 1d). The cylinder has the advantage of not having any in-plane stretching cost, but it has a bending energy penalty that prevents its formation in the bending-dominated limit (see the Appendix).
Figure 2 shows a comparison of the energy landscape for the different structures for fixed values of Δμ~ and λ. The competition between the bulk energy gain, the line tension penalty and the stretching and bending costs will give rise, at the proper conditions, to a barrier that has to be overcome for triggering the formation of these structures. The height of this nucleation barrier and its location, corresponding to the critical cluster size, are mostly controlled by the bulk and line energy contributions, since the critical size typically occurs at small values of x. In terms of shell nucleation, the barrier for the formation of a spherical cap is always the smallest, since the line energy of a circular edge is always smaller than for a rectangular stripe of the same area. Accordingly, the initial embryo of all these structures will be a small spherical cap (Paquay et al., 2017). Neglecting the elastic terms, the critical size for the formation of a spherical shell will be x*≈λ/Δμ~, corresponding to a barrier height for nucleation of Δgcap*≈λ2/(4Δμ~). But rather than on the critical cluster for shell formation, we will be mostly interested in what is the most stable final structure for a given set of conditions.
Figure 2 Download asset Open asset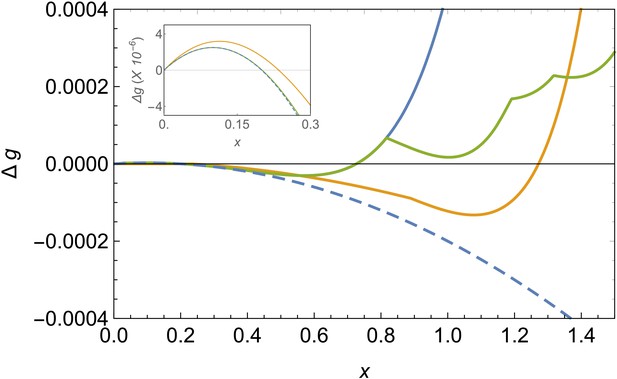
Comparison of free energy landscapes for different structures.
Free energy of formation Δg versus the radius of the patch x in the bending-dominated regime for a defectless spherical shell (blue line), a spherical shell with defects (green), and a ribbon/belt (orange) for λ=0.0001 and Δμ~=0.001. The optimal structure is the one with the minimum energy, which is the belt in this case. The dashed line represents the unfrustrated decrease of energy expected by the classical nucleation picture for the defectless spherical cap in the absence of elastic stresses. The inset zooms the nucleation barrier located at small patch sizes.
Since the free energies of formation only depend on λ and Δμ~ we can draw a universal phase diagram describing what is the structure (i.e. cap with or without defects, ribbon, or belt) with the lowest free energy in its stable size in terms of these two parameters. The term universal is intended to mean that the phase diagram is independent of the details of the capsomer-capsomer interactions such as range, preferred angle between capsomeres, bending rigidity, etc, as we corroborate with a coarse-grained simulation in the next section. Figure 3a shows the phase diagram in the bending-dominated limit, corresponding to γ=0. As can be seen, belts are the most stable structure at low line tension λ and chemical potential differences Δμ~. Closed shells with disclinations are the preferred structure for large values of Δμ~ or λ. The frontier between the belt zone and the cap with disclinations is approximately independent of λ and located at Δμ~≃0.0020. Additionally, a small triangular region where the most stable structure is a frustrated cap with only one disclination is also apparent. As shown in the Appendix, a stable defectless cap only appears as metastable structure, since it has always a larger energy than a belt, and it is thus non competitive as stable structure, even though it may have lower energies as intermediate in the assembly process.
Figure 3 Download asset Open asset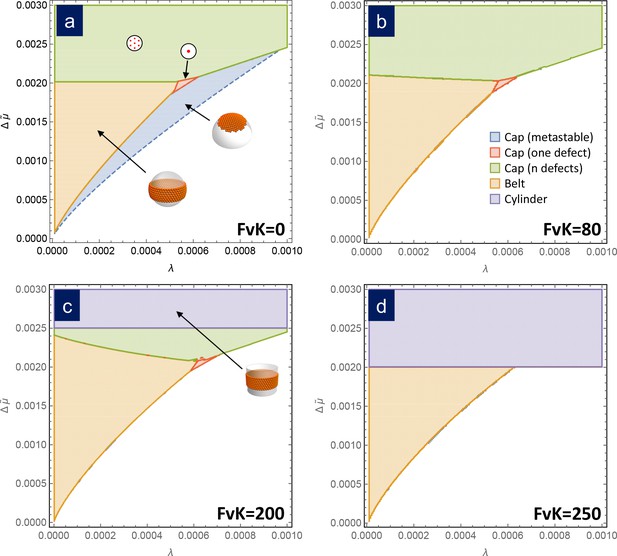
Assembly phase diagrams.
Phase diagrams of the most stable structures in terms of the scaled chemical potential Δμ~ and the scaled line tension λ for different values of the FvK number: a) γ=0, corresponding to the bending-dominated regime, (b) γ=80, (c) γ=200, and d) γ=250. Three possible equilibrium regions are present: belts (i.e. closed ribbons, in orange), frustrated capsids with one defect (red), closed shells with defects (green), and cylinders (purple). Additionally, a region corresponding to a metastable spherical cap without defects (blue) is shown only in (a). In the white region, the equilibrium state corresponds to disaggregated individual capsomers.
Tag » What Is A Viral Capsid
-
Capsid - Wikipedia
-
Viral Capsids: Mechanical Characteristics, Genome Packaging ... - NCBI
-
Virus Capsid - An Overview | ScienceDirect Topics
-
Principles For Enhancing Virus Capsid Capacity And Stability From A ...
-
The Protein Capsid - Virus - Encyclopedia Britannica
-
Capsid | Virus Structure - Britannica
-
Viral Capsid Function & Shapes | What Is A Capsid?
-
Multiple Origins Of Viral Capsid Proteins From Cellular Ancestors - PNAS
-
The Viral Capsid As Novel Nanomaterials For Drug Delivery
-
Viral Capsids And Envelopes: Structure And Function - Lucas
-
Artificial Viral Capsid Dressed Up With Human Serum Albumin
-
Visualization Of Single Molecules Building A Viral Capsid Protein ...
-
Viral Capsid Gene Ontology Term (GO:0019028)