Solution Of Systems Of Linear Inequalities In One Variable - QuickMath

Solution of Systems of Linear inequalities in One Variable

Sometimes it is necessary to find the common solution, or solution set, of two or more inequalities, called a system of inequalities. The solution set of a system of inequality is thus the intersection of the solution set of each inequality in the system.

EXAMPLE Find the solution set of the following system:

6x+3>=2x-5 and 3x-7<5x-9

Solution  

We first find the solution set of each inequality.

6x+3>=2x-5	3x-7<5x-9
4x>=-8	92x<-2
x>=-2	x>1
The Solution set is	The Solution set is

The solution set of the system (Figure 5.7) is

  

       

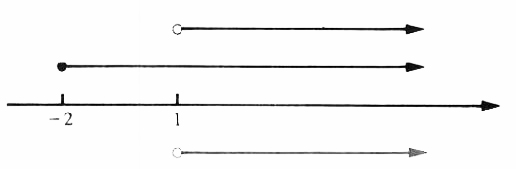
FIGURE 5.7

Let’s see how our Linear inequalities solver solves this and similar problems. Click on "Solve Similar" button to see more examples.

Solve similiar problemEnter your own problem

EXAMPLE Find the solution set of the following system:

4(3-x)<7+3(2-x) and 3(x-1)<4-(1-x)

Solution We first find the solution set of each inequality

      

4(3-x)<7+3(2-x)	3(x-1)<4-(1-x)
12-4x<7+6-3x	3x-3<4-1+x
-x<1	2x<6
x>-1	x<3
The Solution set is	The Solution set is

The solution set of the system (Figure 5.8) is

      

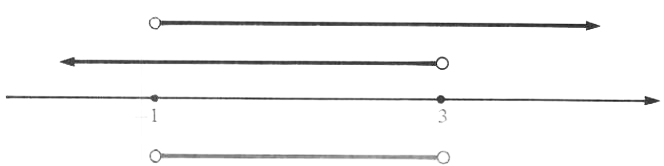
FIGURE 5.8

Let’s see how our Linear inequalities solver generates graph for this and similar problems. Click on "Solve Similar" button to see more examples.

Solve similiar problemEnter your own problem

Solution of Linear Equations with Absolute Values

The absolute value of a number A∈R, denoted by |a|, is either +aor -a whichever is positive, and is zero if a=0

That is,

  

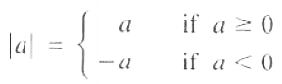
EXAMPLES 1. |6|=6

2. |-4|=-(-4)=4

Note that the absolute value of any real number is either zero or a positive number, never a negative number. That is, |a|>=0 for all a∈R.

When we have the absolute value of a quantity involving a variable such as |x -1| that quantity, x-1. could be

1. greater than or equal to zero, or

2. less than zero.

When x-1 is greater than or equal to zero, that is,

x-1>=0

then |x -1| = x-1

When x-1 is less than zero, that is, x-1<0, then

|x -1| = -(x-1) = -x+1

The following examples illustrate how to solve a linear equation in one variable involving absolute value.

EXAMPLE Solve the equation |x -3| = 5

Solution To find the solution set of this equation, we have to consider two cases

First

When x-3>=0 that is, x>=3

|x -3| = x-3

The equation now becomes

|x -3| = x-3 = 5 or x=8

The solution set is the intersection of the solution sets of

x>=3 and x=8

The solution set (Figure 5.9) is {8}.

  

Figure 5.9

Second When x-3<0 that is, x<3

|x -3| = -(x-3) = -x+3

The equation now becomes

|x -3| = -x+3 = 5 or x = -2

The solution set is the intersection of the solution sets of

x<3 and x=-2

The solution set (Figure 5.10) is {-2}.

  

Figure 5.10

The solution set of |x -3| = 5 is the union of the solution sets in the tow case

Hence the solution set is {-2, 8}.

EXAMPLE Find the solution of |2x+3| = 9.

Solution First:

When 2x+3>=0 that is x>=-(3/2)

|2x+3| = 2x+3

The equation now becomes

|2x+3| = 2x+3 = 9, or x=3

The solution set is the intersection of the solution sets of

x>=-(3/2) and x=3

The solution set (Figure 5.11) is {3}.

  

Figure 5.11

Second: When 2x+3<0, that is, x<-3/2

|2x+3| = -(-2x+3) = -2x-3

The equation now becomes

|2x+3| = -2x-3 = 9, or x=-6

The solution set is the intersection of the solution sets of

x<-3/2 and x=-6

The solution set (Figure 5.12) is {-6}.

  

Figure 5.12

The solution set of |2x+3| = 6 is the union of the solution sets in the tow case

Hence the solution set is {-6, 3}.

Note Since the absolute value of any real number is never negative. the solution set of the equation |3x+5|=-4 is Φ

Find the solution set of |2x-5|=x+3.

First

When 2x-5>=0 that is x>=5/2 (1)

Then |2x-5| = 2x-5

Thus |2x-5| = x+3 becomes

2x-5 = x+3, or x=8 (2)

From (1) and (2) the solution set is {8}.

Second When 2x-5<0, that is, x<5/2; (3)

then |2x-5| = -(2x-5) = -2x+5

Thus, |2x-5| = x+3 becomes

-2x+5 = x+3, or x=2/3 (4)

From (3) and (4) the solution set is {2/3}.

The solution set of |2x-5| = x+3 is the union of the solution sets in the tow case

Hence the solution set is {2/3, 8}.

EXAMPLE Find the solution set of |4-3x| = 3x-4.

Solution First

When 4-3x>=0 that is, x>=4/3 (1)

then |4-3x| = 4-3x

Thus |4-3x| = 3x-4 becomes

4-3x = 3x-4, or x=4-3 (2)

From (1) and (2) the solution set is {4/3}.

Second When 4-3x<0, that is x>4/3; (3)

then |4-3x| = -(4-3x) = -4+3x

Thus |4-3x| = 3x-4 becomes

-4+3x = 3x-4 or 0x=0

Which is true for all x ∈ R (4)

From (3) and (4) the solution set is {x|x>4/3}.

The solution set of |4-3x| = 3x-4 is the union of the solution sets in the tow case

Hence the solution set is

 

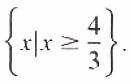
Let’s see how our Linear equations solver solves for this and similar problems. Click on "Solve Similar" button to see more examples.

Solve similiar problemEnter your own problem