SOLVED:Finding The Terminal Point For \pi / 3 Now That You Know The ...

This problem has been solved by verified expert Julie Silva 100% free to try - get full access instantly Start Free Trial

Question

Finding the Terminal Point for $\pi / 3$ Now that you know the terminal point determined by $t=\pi / 6$ , use symmetry to find the terminal point determined by $t=\pi / 3$ (see the figure). Explain your reasoning. Finding the Terminal Point for $\pi / 3$ Now that you know the terminal point determined by $t=\pi / 6$ , use symmetry to find the terminal point determined by $t=\pi / 3$ (see the figure). Explain your reasoning. Algebra and Trigonometry James Stewart,… 2nd Edition Chapter 7, Problem 56 View All Chapters

Step 1

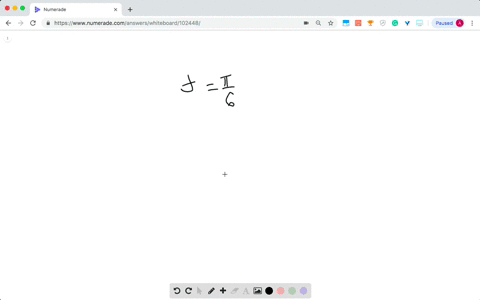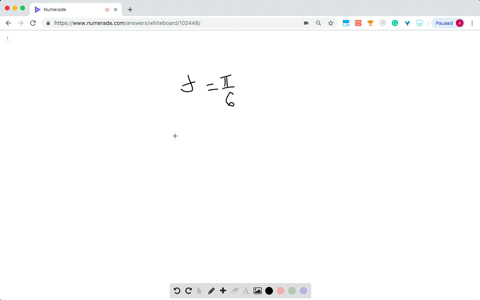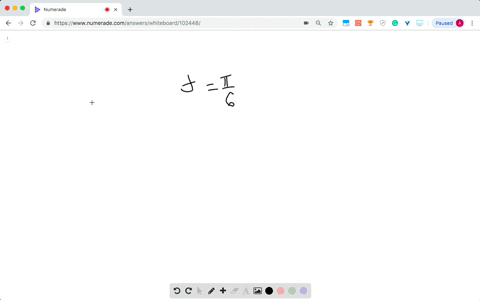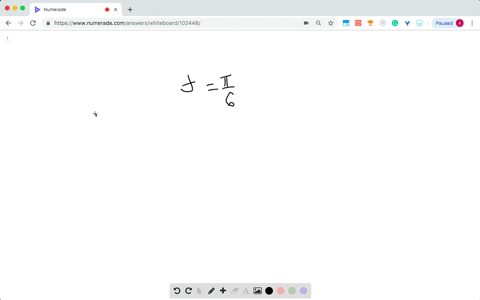
Step 1: First, we recall the terminal point for $\pi / 6$ on the unit circle, which is $(\sqrt{3}/2, 1/2)$. Show more…

Show all steps

Please give Ace some feedback

Your feedback will help us improve your experience

Submit Thanks for your feedback! Finding the Terminal Point for $\pi / 3$ Now that you know the terminal point determined by $t=\pi / 6$ , use symmetry to find the terminal point determined by $t=\pi / 3$ (see the figure). Explain your reasoning. Play audio Feedback Powered by NumerAI

Julie Silva and 101 other Geometry educators are ready to help you.

Ask a new question

Key Concepts

Unit Circle The unit circle is a circle with a radius of one centered at the origin of the coordinate plane. It serves as a foundational concept in trigonometry since each angle in standard position corresponds to a point on the circle, with the x-coordinate representing the cosine of the angle and the y-coordinate representing the sine of the angle. Terminal Point The terminal point of an angle is the point on the unit circle where the terminal side of that angle intersects the circle. This point is crucial as its coordinates (cosine and sine of the angle) define the trigonometric values associated with the angle. Symmetry in the Unit Circle Symmetry in the unit circle refers to the fact that the circle is symmetric about the x-axis, y-axis, and the origin. This property allows one to determine the coordinates of terminal points for related angles by reflecting a known point across these axes. For example, if the terminal point of one angle is known, symmetry can be used to find the terminal point for another angle that is a mirror image with respect to an axis. Reference Angle A reference angle is the acute angle formed by the terminal side of an angle and the horizontal axis. It simplifies the process of finding trigonometric values for angles outside the first quadrant because these values can be derived from the corresponding acute angle, with appropriate sign adjustments based on the quadrant in which the original angle lies.

Recommended Videos

DISCOVER = PROVE: Finding the Terminal Point for $\pi / 3$ Now that you know the terminal point determined by $t=\pi / 6,$ use symmetry to find the terminal point determined by $t=\pi / 3$ (see the figure). Explain your reasoning.

Trigonometric Functions: Unit Circle Approach

The Unit Circle

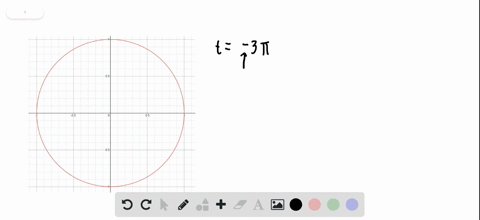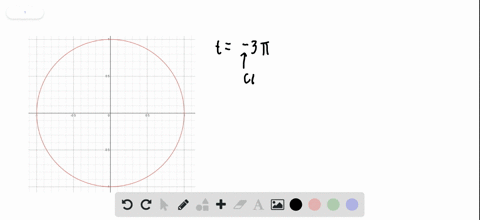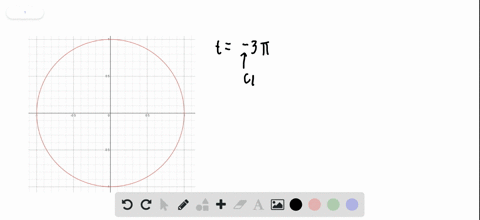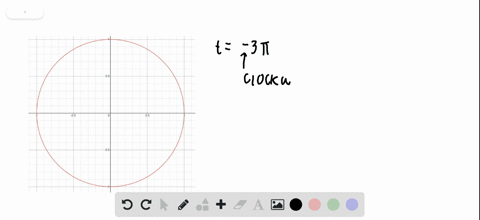
Terminal Points Find the terminal point $P(x, y)$ on the unit circle determined by the given value of $t .$ $$ t=-3 \pi $$

Trigonometric Functions: Unit Circle Approach

The Unit Circle

Terminal Points Find the terminal point $P(x, y)$ on the unit circle determined by the given value of $t .$ $$ t=\frac{3 \pi}{2} $$

Trigonometric Functions: Unit Circle Approach

The Unit Circle

Transcript

00:01 So in this problem, we are told that we know the terminal point determined by t equals pi over 6. 00:05 Well, first off, let's recall what that is. 00:07 Remember, pi over 6 is equivalent to a 30 -degree angle. 00:11 So if we're thinking about our terminal point, that would mean that our x value is 1 half, or sorry, root 3 over 2, switching it here, and that the y value is 1 half. 00:24 So now we want to use this information in order to find the terminal point for t equals pi over 3. 00:31 Well, let's think about where this point would go in terms of our coordinate plane. 00:35 Well, as we mentioned before, pi over 6 is a 30 -degree angle. 00:38 So that would be something like this. 00:40 So this is 30 degrees. 00:41 That gives us this terminal point on our unit circle, root 3 over 2, comma 1 half... Need help? Use Ace Ace is your personal tutor. It breaks down any question with clear steps so you can learn. Start Using Ace Ace is your personal tutor for learning Step-by-step explanations Instant summaries Summarize YouTube videos Understand textbook images or PDFs Study tools like quizzes and flashcards Listen to your notes as a podcast

What our educators say

25992 Students Helped in Geometry “Numerade has a great goal - to increase people's educational levels all around the world. Educators do not complete student's personal homework tasks. We create video tutorials that may be used for many years in the future.” Dr. Mei Lin Chen PhD in Geometry

44601 Students Helped in Geometry "The format has forced me to think about what knowledge is needed by the student to solve a problem and present it concisely and understandably within the time constraint of the video." Dr. Emily Green PhD in Geometry

30417 Students Helped in Geometry “Explaining topics while I make Numerade videos has helped me deepen my own understanding and come up with new ways to help my students grasp concepts while I'm teaching.” Professor Jonathan Reed Master's in Geometry

Get step-by-step video solutionfrom top educators Start your free 7-day trial, Sign up now. Continue with Facebook Continue with Apple Continue with Clever or Name Email Password Create Account By creating an account, you agree to the Terms of Service and Privacy Policy Already have an account? Log In A free answerjust for you

Watch the video solution with this free unlock.

View the Answer

Log in to watch this video ...and 100,000,000 more!

EMAIL

PASSWORD

Log in OR Continue with Facebook Continue with Apple Continue with Clever Don't have an account? Sign Up