Standard Form Of Quadratic Equation - Formula, Calculator, Examples

Standard Form of Quadratic Equation

The standard form of quadratic equation is ax2 + bx + c = 0, where 'a' is the leading coefficient and it is a non-zero real number. This equation is called 'quadratic' as its degree is 2 because 'quad' means 'square'. Apart from the standard form of quadratic equation, a quadratic equation can be written in other forms.

• Vertex Form: a (x - h)2 + k = 0
• Intercept Form: a (x - p)(x - q) = 0

Let us learn more about the standard form of a quadratic equation and let us see how to convert one form of a quadratic equation into another.

1.	What is the Standard Form of Quadratic Equation?
2.	Converting Standard Form of Quadratic Equation into Vertex Form
3.	Converting Standard Form of Quadratic Equation into Intercept Form
4.	FAQs on Standard Form of Quadratic Equation

What is the Standard Form of Quadratic Equation?

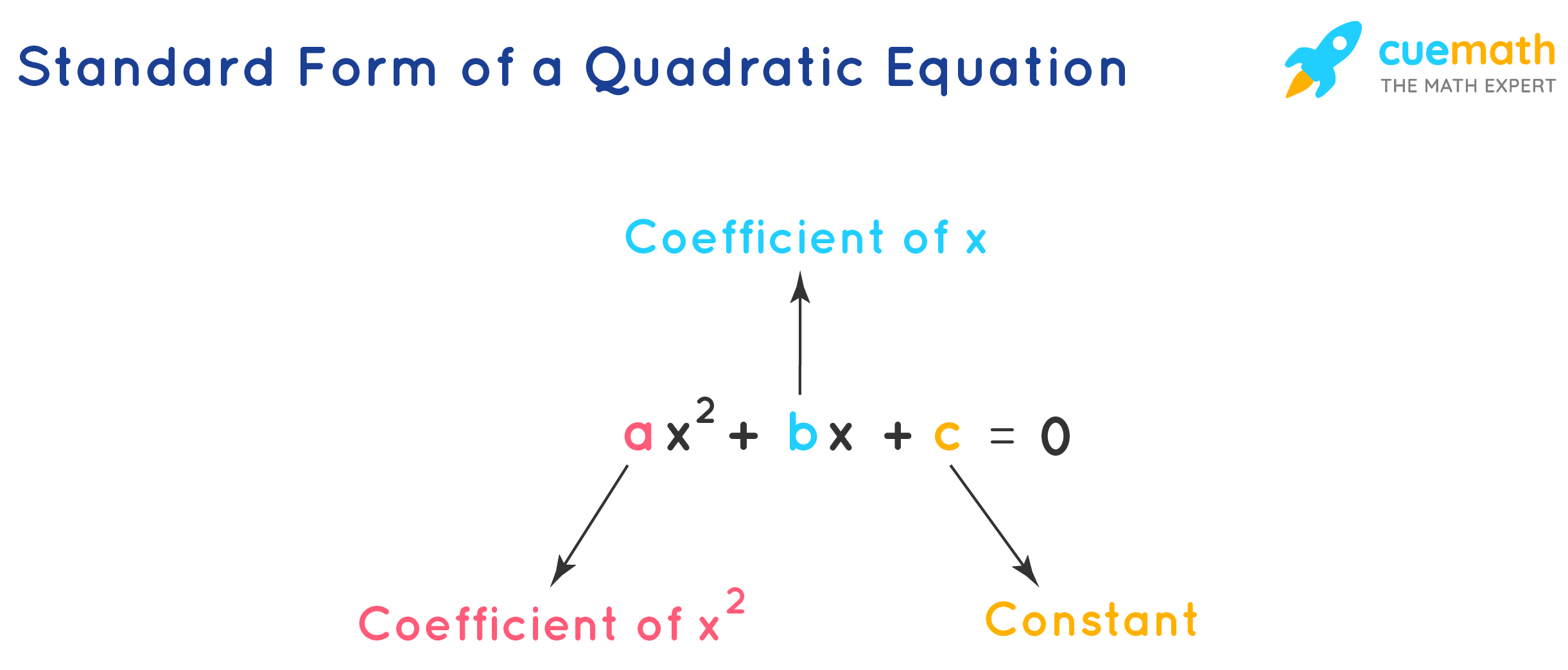
The standard form of quadratic equation with a variable x is of the form ax2 + bx + c = 0, where a ≠ 0, and a, b, and c are real numbers. Here, b and c can be either zeros or non-zero numbers and

• 'a' is the coefficient of x2
• 'b' is the coefficient of x
• 'c' is the constant

Examples of Standard Form of Quadratic Equation

Here are some examples of quadratic equations in standard form.

• 2x2 - 7x + 8 = 0
• (-1/3) x2 + 2x - 1 = 0
• √2 x2 - 8 = 0
• -3x2 + 8x = 0

General Form of Quadratic Equation

The standard form of a quadratic equation is also known as its general form. Thus, the general form of a quadratic equation is also of the form ax2 + bx + c = 0, where a ≠ 0.

Converting Standard Form of Quadratic Equation into Vertex Form

Let us convert the standard form of a quadratic equation ax2 + bx + c = 0 into the vertex form a (x - h)2 + k = 0 (where (h, k) is the vertex of the quadratic function f(x) = a (x - h)2 + k). Note that the value of 'a' is the same in both equations. Let us just set them equal to know the relation between the variables.

ax2 + bx + c = a (x - h)2 + k ax2 + bx + c = a (x2 - 2xh + h2) + k ax2 + bx + c = ax2 - 2ah x + (ah2 + k)

Comparing the coefficients of x on both sides, b = -2ah ⇒ h = -b/2a ... (1)

Comparing the constants on both sides, c = ah2 + k c = a (-b/2a)2 + k (From (1)) c = b2/(4a) + k k = c - (b2/4a) k = (4ac - b2) / (4a)

Thus, we can use the formulas h = -b/2a and k = (4ac - b2) / (4a) to convert the standard to vertex form.

Example of Converting Standard Form to Vertex Form

Consider the quadratic equation 2x2 - 4x + 3 = 0. Comparing this with ax2 + bx + c = 0, we get a = 2, b = -4, and c = 3. To convert it into the vertex form, let us find the values of h and k.

• h = -b/2a = -(-4) / (2 · 2) = 1
• k = (4ac - b2) / (4a) = (4 · 2 · 3 - (-4)2) / (4 · 2) = (24 - 16) / 8 = 1

Substituting a = 2, h = 1, and k = 1 in the vertex form a (x - h)2 + k = 0, we get:

2 (x - 1)2 + 1 = 0

Converting Vertex Form to Standard Form

The process of converting the vertex form of a quadratic equation into the standard form is pretty simple and it is done by simply evaluating (x - h)2 = (x - h) (x - h) and simplifying. Let us consider the above example 2 (x - 1)2 + 1 = 0 and let us convert it back into standard form.

2 (x - 1)2 + 1 = 0 -------> Vertex Form 2 (x - 1) (x - 1) + 1 = 0 2 (x2 - x - x + 1) + 1 = 0 2 (x2 - 2x + 1) + 1 = 0 2x2 - 4x + 2 + 1 = 0 2x2 - 4x + 3 = 0 --------> Standard Form

Converting Standard Form of Quadratic Equation into Intercept Form

Let us convert the standard form of a quadratic equation ax2 + bx + c = 0 into the vertex form a (x - p)(x - q) = 0. Here, (p, 0) and (q, 0) are the x-intercepts of the quadratic function f(x) = ax2 + bx + c) and hence p and q are the roots of the quadratic equation. Thus, we just use any one of the solving quadratic equation techniques to find p and q.

Example to Convert Standard to Intercept Form

Consider the quadratic equation in standard form 2x2 - 7x + 5 = 0. By comparing this with ax2 + bx + c = 0, we get a = 2. Now we will solve the quadratic equation by factorization.

2x2 - 7x + 5 = 0 2x2 - 2x - 5x + 5 = 0 2x (x - 1) - 5 (x - 1) = 0 (x - 1) (2x - 5) = 0 x - 1 = 0; 2x - 5 =0 x = 1; x = 5/2

Thus, p = 1 and q = 5/2

Thus, the intercept form is, a (x - p)(x - q) = 0 2 (x - 1) (x - 5/2) = 0 2 (x - 1) (2x - 5)/2 = 0 (x - 1) (2x - 5) = 0

Converting Intercept Form to Standard Form

The process of converting the intercept form of a quadratic equation into standard form is really easy and it is done by simply multiplying the binomials (x - p) (x - q) and simplifying. Let us consider the above example (x - 1) (2x - 5) = 0 and let us convert it back into standard form.

(x - 1) (2x - 5) = 0 -------> Intercept Form 2x2 - 5x - 2x + 5 = 0 2x2 - 7x + 5 = 0 --------> Standard Form

Important Notes on Standard Form of Quadratic Equation:

• A quadratic equation in standard form is ax2 + bx + c = 0.
• A quadratic equation in vertex form is a (x - h)2 + k = 0, where h = -b/2a and k = (4ac - b2) / (4a).
• A quadratic equation in intercept form is a (x - p)(x - q) + k = 0, where p and q are the roots of the quadratic equation.

☛Related Topics:

• Quadratic Expressions
• Multiplying Binomials Calculator
• Quadratic Equation Calculator
• Roots of Quadratic Equation Calculator

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.