Surface Area Calculator

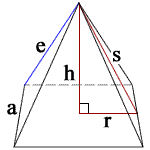h = height s = slant height a = side length e = lateral edge length r = a/2 V = volume Stot = total surface area Slat = lateral surface area Sbot = bottom surface area

Calculate more with Pyramid Calculator

Online calculator to calculate the surface area of geometric solids including a capsule, cone, frustum, cube, cylinder, hemisphere, pyramid, rectangular prism, sphere, spherical cap, and triangular prism

Units: Note that units are shown for convenience but do not affect the calculations. The units are in place to give an indication of the order of the results such as ft, ft2 or ft3. For example, if you are starting with mm and you know r and h in mm, your calculations will result with V in mm3 and S in mm2.

Below are the standard formulas for surface area.

Surface Area Formulas:

Capsule Surface Area

• Volume = πr2((4/3)r + a)
• Surface Area = 2πr(2r + a)

Circular Cone Surface Area

• Volume = (1/3)πr2h
• Lateral Surface Area = πrs = πr√(r2 + h2)
• Base Surface Area = πr2
• Total Surface Area = L + B = πrs + πr2 = πr(s + r) = πr(r + √(r2 + h2))

Circular Cylinder Surface Area

• Volume = πr2h
• Top Surface Area = πr2
• Bottom Surface Area = πr2
• Total Surface Area = L + T + B = 2πrh + 2(πr2) = 2πr(h+r)

Conical Frustum Surface Area

• Volume = (1/3)πh (r12 + r22 + (r1 * r2))
• Lateral Surface Area = π(r1 + r2)s = π(r1 + r2)√((r1 - r2)2 + h2)
• Top Surface Area = πr12
• Base Surface Area = πr22
• Total Surface Area = π(r12 + r22 + (r1 * r2) * s) = π[ r12 + r22 + (r1 * r2) * √((r1 - r2)2 + h2) ]

Cube Surface Area

• Volume = a3
• Surface Area = 6a2

Hemisphere Surface Area

• Volume = (2/3)πr3
• Curved Surface Area = 2πr2
• Base Surface Area = πr2
• Total Surface Area= (2πr2) + (πr2) = 3πr2

Pyramid Surface Area

• Volume = (1/3)a2h
• Lateral Surface Area = a√(a2 + 4h2)
• Base Surface Area = a2
• Total Surface Area = L + B = a2 + a√(a2 + 4h2)) = a(a + √(a2 + 4h2))

Rectangular Prism Surface Area

• Volume = lwh
• Surface Area = 2(lw + lh + wh)

Sphere Surface Area

• Volume = (4/3)πr3
• Surface Area = 4πr2

Spherical Cap Surface Area

• Volume = (1/3)πh2(3R - h)
• Surface Area = 2πRh

Triangular Prism Surface Area

Top Surface Area of a Triangular Prism Formula

\[ A_{top} = \dfrac{1}{4} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \] \[ A_{top} = \dfrac{1}{4} \sqrt{\begin{aligned}(a+&b+c)(b+c-a)\\&\times(c+a-b)(a+b-c)\end{aligned}} \]

Bottom Surface Area of a Triangular Prism Formula

\[ A_{bot} = \dfrac{1}{4} \sqrt{(a+b+c)(b+c-a)(c+a-b)(a+b-c)} \] \[ A_{bot} = \dfrac{1}{4} \sqrt{\begin{aligned}(a+&b+c)(b+c-a)\\&\times(c+a-b)(a+b-c)\end{aligned}} \]

Lateral Surface Area of a Triangular Prism Formula

\[ A_{lat} = h (a+b+c) \]

Total Surface Area of a Triangular Prism Formula

\[ A_{tot} = A_{top} + A_{bot} + A_{lat} \]