Trapezoid - Shape, Properties, Formula, Definition, Examples

Trapezoid

The trapezoid is fascinating because it is defined based on the geography you belong to. If you’re visiting the United Kingdom on an exchange trip and ask a student to draw a trapezoid for you, then they will draw it like a trapezium. A trapezoid is also called a trapezium in some parts of the world and it is a type of quadrilateral with one pair of opposite sides parallel to each other.

1.	What is Trapezoid?
2.	Properties of Trapezoid
3.	Types of Trapezoids
4.	Trapezoid Formula
5.	FAQs on Trapezoid

What is Trapezoid?

A trapezoid is also known as a trapezium is a four-sided polygon or a quadrilateral. It has one set of opposite sides which are parallel and a set of non-parallel sides. The parallel sides are known as the bases and the non-parallel sides are known as the legs of the trapezoid.

Definition of Trapezoid

A trapezoid is a four-sided closed 2D figure which has an area and its perimeter. Two sides of the shape are parallel to each other and they are termed as the bases of the trapezoid. The non-parallel sides are known as the legs or lateral sides of a trapezoid. The shortest distance between two parallel sides is known as the altitude. Since the opposite sides are parallel to each other, calculating the area of a trapezoid is simple.

Properties of Trapezoid

These are the properties of a trapezoid that make it stand out from other quadrilaterals:

• The bases (the top and bottom) are parallel to each other
• Opposite sides of a trapezoid (isosceles) are of the same length
• Angles next to each other sum up to 180°
• The median is parallel to both the bases
• Median's length is the average of both the bases i.e. (a +b)/2
• If both pairs of the opposite sides are parallel in a trapezoid, it is considered a parallelogram
• If both pairs of the opposite sides are parallel, all sides are of equal length, and at right angles to each other, then a trapezoid can be considered as a square
• If both pairs of the opposite sides are parallel, its opposite sides are of equal length and at right angles to each other, then a trapezoid can be considered as a rectangle

Types of Trapezoids

There are three types of trapezoids, and those are given below:

1. Isosceles Trapezoid
2. Scalene Trapezoid
3. Right Trapezoid

Isosceles Trapezoid

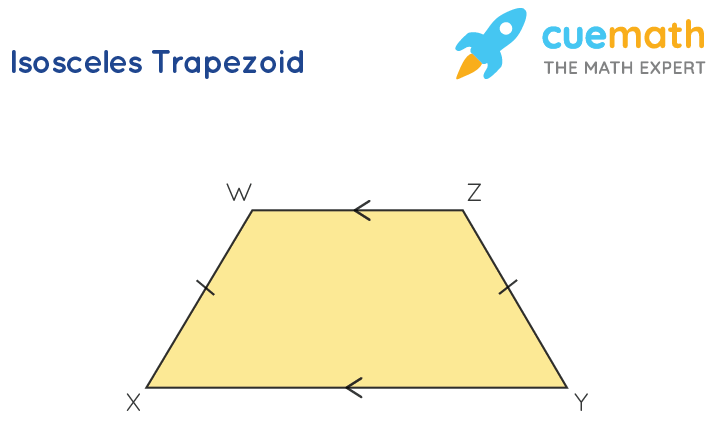
If the legs or non-parallel sides of the trapezoid are equal in length, then it is called an isosceles trapezoid. The angles of the parallel sides (base) in the isosceles trapezoid are equal to each other. An isosceles trapezoid has a line of symmetry and both the diagonals are equal in length.

In the below isosceles trapezoid XYZW, XY and WZ are called the bases of the trapezoid. WX and YZ are called the legs of the trapezoid since they are not parallel to each other.

Scalene Trapezoid

When neither the sides nor the angles of the trapezoid are equal, then it is a scalene trapezoid. In the below scalene trapezoid, all four sides i.e. AB, BC, CD, and DA are of different lengths. The bases i.e. DC and AB are parallel to each other but are of different lengths.

Right Trapezoid

A right trapezoid also called the right-angled trapezoid, has a pair of right angles. These kinds of trapezoids are used to estimate the areas under the curve. In the below right trapezoid or right-angled trapezoid, there are two right angles one at D and the other one at A. One pair of opposite sides i.e. DC and AB are parallel to each other.

Trapezoid Formula

There are two main trapezoid formulas, they are:

• Area of a Trapezoid
• Perimeter of a Trapezoid

Area of Trapezoid

The area of the trapezoid is calculated by measuring the average of the parallel sides and multiplying it with its height. To find the area of a trapezoid, the lengths of two of its parallel sides is to be known and the distance (height) between them. It is the number of unit squares that can be fit inside the shape and it is measured in square units such as cm2, m2, in2, etc. The formula of the area (A) of a trapezoid is calculated on the bases i.e. a and b and whose height is h which is the perpendicular distance between a and b.

Hence, the area of a trapezoid is calculated by the following formula:

Area =[(AB + CD)/2] × h

A = [(a + b)/2] × h

Where,

• AB and CD = parallel sides
• a = shorter base
• b = longer base
• h = height or altitude

Perimeter of Trapezoid

The perimeter of a trapezoid is defined as the total length of the boundary of the shape, i.e. the sum of all its sides. Since the trapezoid is a two-dimensional shape, thus, the perimeter will also lie in a two-dimensional plane only. Consider a trapezoid ABCD as shown below with side measures a,b,c, and d. Let's look into the Trapezoid Formula. The perimeter of the trapezoid formula is calculated by finding the sum of all the sides i.e, AB + BC + CD + DA

Perimeter of a Trapezoid = Sum of all the sides = a + b + c + d

where, a, b,c, and d are the sides of the trapezoid.

☛Related Topics on Trapezoid

Listed below are a few topics that are related to a trapezoid.

• Trapezoid Worksheets
• Perimeter of a Trapezoid Calculator
• Rhombus
• Square
• 3D shapes