Triangle Congruence Postulates - ASA & AAS Explained (2019)

In today’s geometry lesson, we’re going to learn two more triangle congruency postulates.

Jenn, Founder Calcworkshop®, 15+ Years Experience (Licensed & Certified Teacher)

The Angle-Side-Angle and Angle-Angle-Side postulates.

These postulates (sometimes referred to as theorems) are know as ASA and AAS respectively.

Here we go!

Triangle Congruence Postulates

Proving two triangles are congruent means we must show three corresponding parts to be equal.

From our previous lesson, we learned how to prove triangle congruence using the postulates Side-Angle-Side (SAS) and Side-Side-Side (SSS). Now it’s time to look at triangles that have greater angle congruence.

Angle-Side-Angle

The Angle-Side-Angle Postulate (ASA) states that if two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the two triangles are congruent.

And as seen in the figure to the right, we prove that triangle ABC is congruent to triangle DEF by the Angle-Side-Angle Postulate.

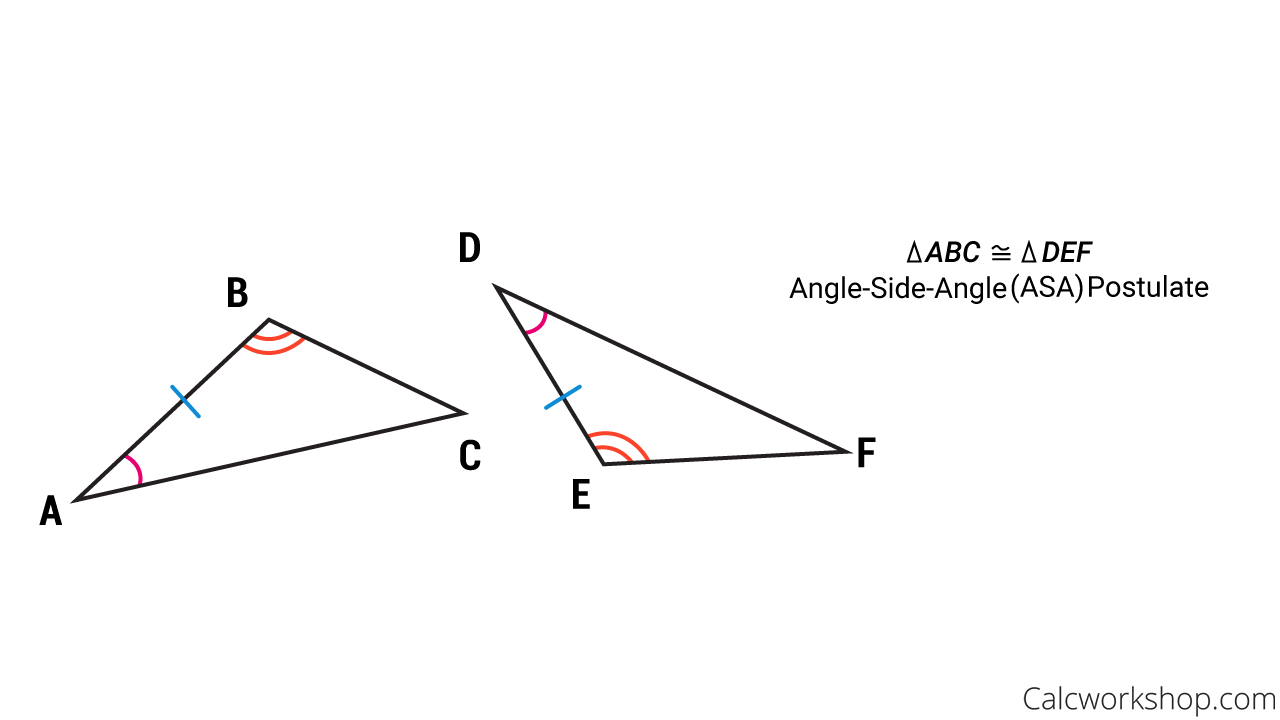
ASA Postulate Example

Angle-Angle-Side

Whereas the Angle-Angle-Side Postulate (AAS) tells us that if two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the two triangles are congruent.

And as seen in the accompanying image, we show that triangle ABD is congruent to triangle CBD by the Angle-Angle-Side Postulate.

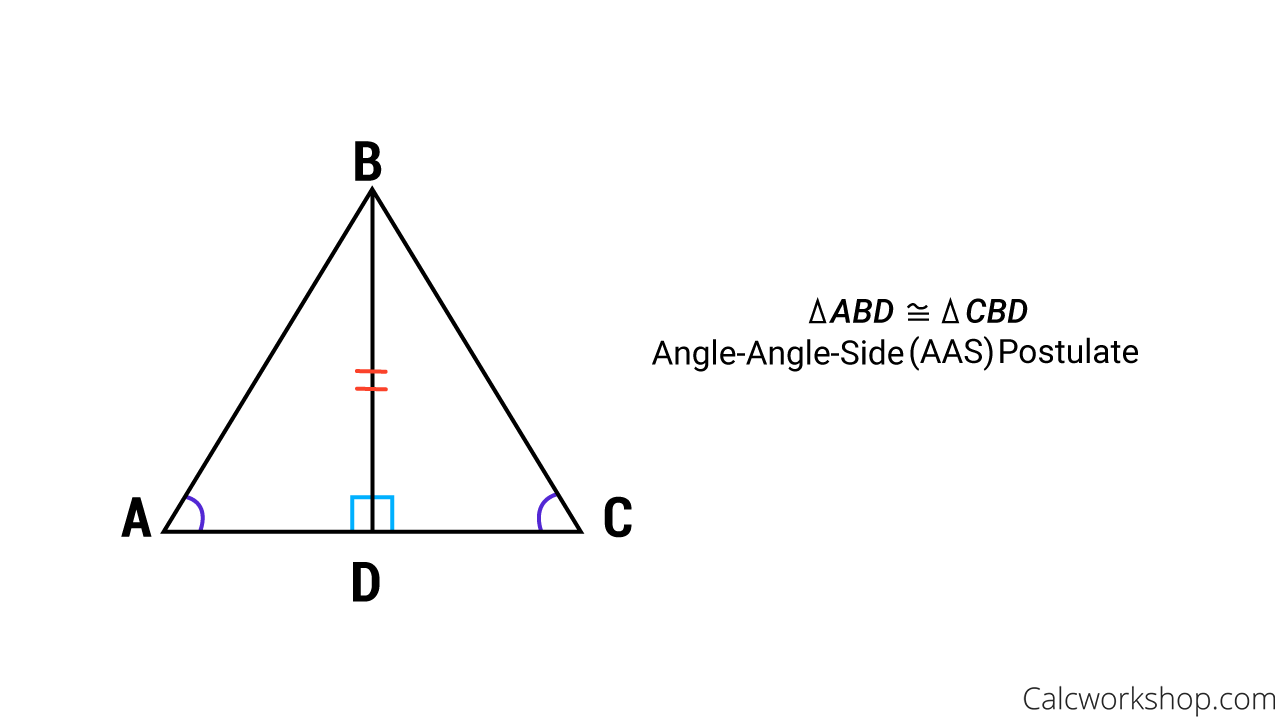
AAS Postulate Example

As you will quickly see, these postulates are easy enough to identify and use, and most importantly there is a pattern to all of our congruency postulates.

Can you can spot the similarity?

• SAS
• SSS
• ASA
• AAS

Yep, you guessed it. Every single congruency postulate has at least one side length known!

And this means that AAA is not a congruency postulate for triangles. Likewise, SSA, which spells a “bad word,” is also not an acceptable congruency postulate.

We will explore both of these ideas within the video below, but it’s helpful to point out the common theme.

You must have at least one corresponding side, and you can’t spell anything offensive!

Knowing these four postulates, as Wyzant nicely states, and being able to apply them in the correct situations will help us tremendously throughout our study of geometry, especially with writing proofs.

So together we will determine whether two triangles are congruent and begin to write two-column proofs using the ever famous CPCTC: Corresponding Parts of Congruent Triangles are Congruent.

Triangle Congruency – Lesson & Examples (Video)

38 min

• Introduction ASA and AAS postulates
• 00:00:24 – What are Angle-Side-Angle and Angle-Angle-Side postulates?
• 00:13:17 – If possible, write a congruency statement using ASA, AAS, SSS, or SAS (Examples #1-6)
• Exclusive Content for Member’s Only

• 00:28:41 – If possible, write a congruency statement using AAS, ASA, SAS, or SSS (Examples #7-10)
• 00:40:18 – Complete the two column proof (Examples #11-13)
• Practice Problems with Step-by-Step Solutions
• Chapter Tests with Video Solutions

Get access to all the courses and over 450 HD videos with your subscription

Monthly and Yearly Plans Available

Get My Subscription Now

Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.