Volume Of Triangular Prism - Formula, Definition, Examples - Cuemath

Volume of Triangular Prism

The volume of a triangular prism is the space occupied by it from all three dimensions. A prism is a solid object which has identical bases, flat rectangular side faces, and the same cross-section all along its length. There are different types of prisms that are classified and named as per the shape of their base. A triangular prism has 2 identical triangular bases and 3 rectangular lateral faces.

1.	What is the Volume of a Triangular Prism?
2.	Volume of Triangular Prism Formula
3.	How to find the Volume of Triangular Prism?
4.	FAQs on Volume of Triangular Prism

What is the Volume of a Triangular Prism?

The volume of a triangular prism can be calculated by taking the product of the area of the triangular base and the height of the prism which is also known as the length of the prism. For this, let us first understand what a triangular prism looks like.

Definition of Triangular Prism

A triangular prism is a polyhedron made up of two triangular bases and three rectangular sides. Or, it can be considered as a pentahedron (as it has 5 faces altogether) wherein the edges and vertices of the bases are joined with each other by three rectangular sides. By definition, the two triangular bases are parallel and congruent to each other. It has:

• 2 bases (which are congruent triangles)
• 3 side faces (which are congruent rectangles)
• Total number of faces - 5
• 9 edges
• 6 corners or vertices

The length of the triangular prism is the perpendicular distance between the centers of the two bases. It is represented by "l" in the figure given below.

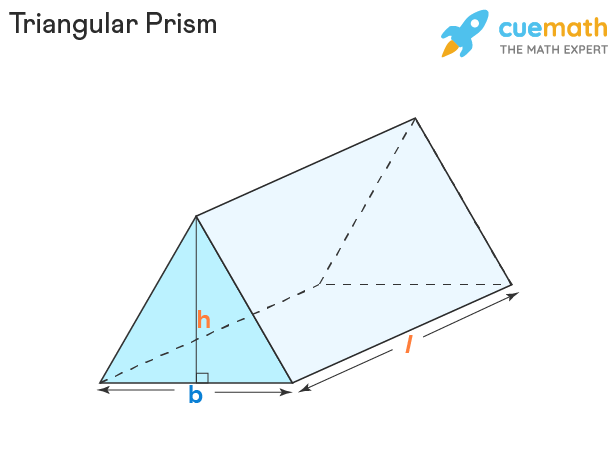
Observe the triangular prism shown above where 'b' is the base of each side of two congruent triangles, 'h' is the height of the base triangle, and 'l' is the length of the prism.

Volume of Triangular Prism Formula

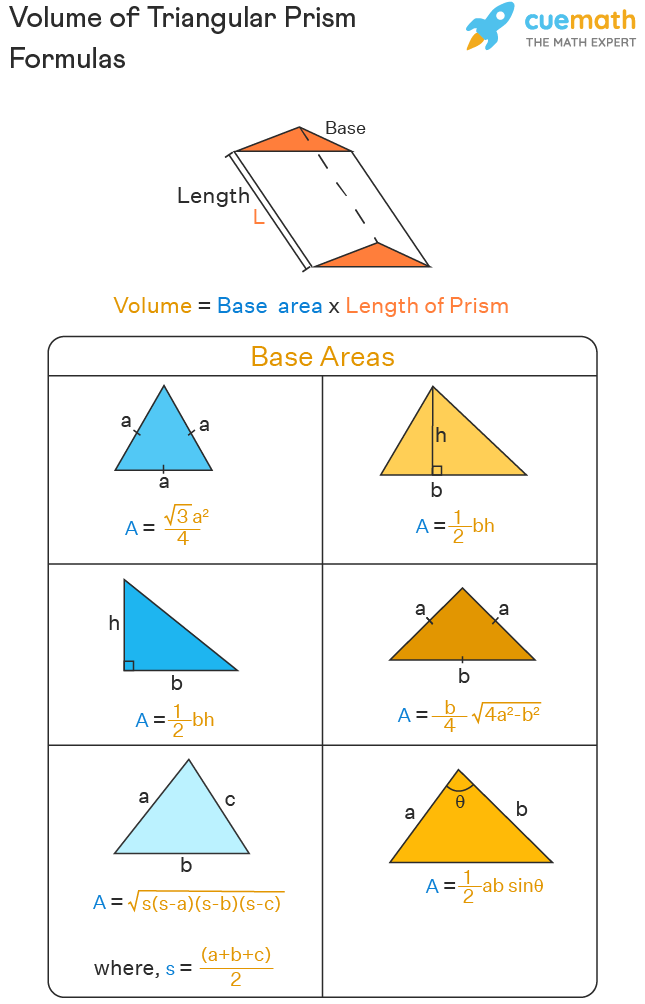
The volume of a triangular prism is the space inside it or the space occupied by it. It is measured in cubic units such as cm3, m3, in3, etc. We will see the formulas to calculate the volumes of different types of triangular prisms. The volume of any prism is obtained by multiplying its base area by its length.

The volume of a prism = base area × length of the prism

We will use this formula to calculate the volume of a triangular prism as well. We know that the base of a triangular prism is a triangle. By applying the above formula to a triangular prism, we get,

Volume of a triangular prism = area of base triangle × length of the prism

Here, we can find the area of the base triangle based on its type and the available information. The following list shows the formulas to find the area of the base triangle.

• If the base triangle is an equilateral triangle (in this case, the prism is called equilateral triangular prism) with each side 'a', then its area = √3a2/4
• If the triangle's base 'b' and height 'h' are given, then its area = (1/2) bh
• If the base triangle is a right-angled triangle (in this case, the prism is called a right triangular prism) with two legs 'b' and 'h' then its area = (1/2) bh
• If the base triangle is an isosceles triangle with its sides to be 'a', 'a', and 'b' then its area is (b/4) × √(4a2 - b2)
• If the base triangle is a scalene triangle where all three sides 'a', 'b', and 'c' are given, then its area is calculated using √[s(s-a)(s-b)(s-c)]; where, s = (a + b + c)/2. Note that you can apply this formula (which is also called Heron's formula) for an isosceles triangle (or) an equilateral triangle as well.
• If the base triangle's two sides 'a' and 'b' and the included angle 'θ' are given, then its area is found using 1/2 ab sin θ

How to Find the Volume of Triangular Prism?

The volume of a triangular prism can be calculated with the help of the following steps and the example given below. Before that make sure that all measurements are of the same units.

• Step 1: Identify the type of the base triangle and find its area using a suitable formula (as explained in the previous section).
• Step 2: Identify the length of the prism (Note that this length of the prism is also known as the height of the prism, and it should not be confused with the height of the base triangle).
• Step 3: Multiply the base area (from step 1) and the length of the prism to find the volume.

Example: Calculate the volume of the triangular prism whose length is 15 in and whose base is an equilateral triangle of side 6 inches.

Solution: The volume of the triangular prism can be calculated using the following steps.

• Step 1: The base triangle is an equilateral triangle with its side as a = 6. So its area is found using the formula, √3a2/4 = √3(6)2/4 = 9√3 square inches.
• Step 2: The length of the prism is 15 in.
• Step 3: The volume of the given triangular prism = base area × length = 9√3 × 15 = 135√3 cubic inches.

Tips on Volume of Triangular Prism

• The length of a triangular prism is also known as the height of the prism.
• This height of the prism should not be confused with the height of the base triangle.

☛ Related Articles

• Volume of 3D Shapes
• Volume of Cube
• Volume of Cylinder
• Volume of Cuboid
• Volume of Sphere
• Volume of Rectangular Prism

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12. Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.