What Is A Central Angle? - [ Formula & Circle Calculations Explained ...

What is a Central Angle?

Contents

Definition: A central angle is an angle whose vertex is the center O of a circle and whose legs are radii intersecting the circle in two different points on the circumference of the circle.

The central angle is also known as the arc’s angular distance.

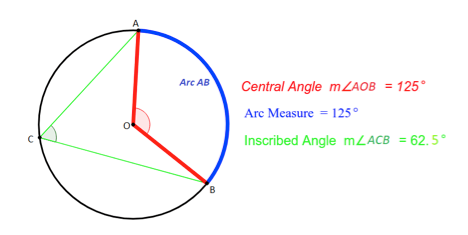
Central Angle of a Circle

Characteristics

A central angle is an angle formed by two radii with the vertex at the center of the circle.

•  The angle measure of the central angle is congruent to the measure of the intercepted arc. Central angle = Intercepted arc m∠AOB= m (AB) ̂ (In the above diagram)
• In congruent circles or in a circle, congruent central angles have congruent arcs (and vice versa).
• In congruent circles or in a circle, congruent central angles have congruent chords (and vice versa).
• The measure of central angle is twice the measure of the inscribed angle subtended by the same arc. (An inscribed angle is an angle whose vertex lies on the circumference of the circle.)
• The sum of the measures of the central angles of a circle with no common points is 360°.

Uses

The central angle theorem is very useful in solving questions that deals with angles within circles. By using the central angle theorem, many complicated circle questions can be simplified into a simple one. The central angle theorem is central to many circle questions.

Importance

Central angle is equal to the arc length. Therefore, to find arc length and area of the sector, central angle plays the most important role. If we know the central angle, we can find both arc length and area of sector. Arc length is the portion of a circumference of a circle made by the central angle. Area of sector is the region bounded by the two radii and the arc length lie between these two radii.

Central Angle Formula

The central angle formula is calculated using the arc measure and inscribed angle of a circle.

The angle measure of the central angle is congruent to the measure of the intercepted arc.

Central angle = Intercepted arc

The measure of central angle is twice the measure of the inscribed angle subtended by the same arc.

Central angle = 2 (inscribed angle)

Central angle (in radians) = (Arc Length)/Radius

Central angle (in radians) = (2 (area of sector))/〖(Radius)〗^2

Central Angle Theorems

Circle theorems involving Central Angle

• The measure of an arc of a circle is congruent to the measure of the central angle that intercepts the arc.
• If a central angle and an inscribed angle subtended by the same arc, central angle is twice the inscribed angle.

•  In a circle or in congruent circles, congruent central angles have congruent arcs. Converse: In a circle, or in congruent circles, congruent arcs have congruent central angles. In the circle shown above, (BC) ̂ ≅ (DE) ̂ if and only if ∠BAC ≅ ∠DAE.

• In a circle or in congruent circles, congruent central angles have congruent chords. Converse: In a circle, or in congruent circles, congruent chords have congruent central angles. In the circle shown above, chord (BC) ̅= chord (DE) ̅ if and only if ∠BAC ≅ ∠DAE.

Calculating Central Angle and Intercepted Arc

Here’s how to find the central angle of a circle.

Intercepted arc formula

• The central angle = the measure of the intercepted arc
• 2(the inscribed angle) = the central angle
• 2(the inscribed angle) = the intercepted arc
• The inscribed angle = half the sum of the intercepted arcs

Example 1

Determine the value of a in the circle shown below.

Solution:

The central angle = intercepted arc 60° = (4a + 8)°

Simplify:

4a + 8 = 60

Subtract 8 both sides

4a = 52

Divide both sides by 4

a = 13

Example 2

Determine the measure of ∠AOB in the circle shown below.

Solution:

∠AOB is a central angle and ∠ACB is an inscribed angle subtended on the same arc AB.

We know that the central angle is twice the inscribed angle if they are subtended on the same arc.

Therefore,

∠AOB = 2∠ACB

∠AOB = 2(64°)

∠AOB = 128°

Example 3

Determine the measure of arc DC in the circle shown below.

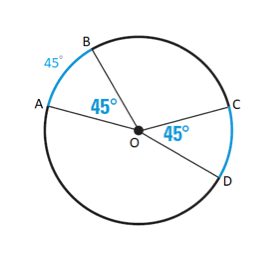
Solution:

We know that In a circle, congruent central angles have congruent arcs.

In the given circle, central angles are congruent

∠AOB ≅ ∠COD

Therefore their intercepted arc should have to be congruent.

(AB) ̂ = (CD) ̂

(AB) ̂ = 45° (given)

(CD) ̂ = 45°

Example 4

Determine the value of x, if the ∠AOB ≅ ∠COD, and chord AB = 6.

Solution:

In a circle congruent central angles have congruent chords.

In the given circle, ∠AOB and ∠CODare central angles

It is given that ∠AOB ≅ ∠COD.

Therefore,

Chord AB ≅ Chord CD

Chord AB = 6 (given)

Chord CD = 6.