What Is A Diagonal, Definition, Examples, Facts & Formula - Cuemath

Diagonals

A diagonal is a line segment that joins one corner (vertex) of a polygon to another but is not an edge (side). In other words, it joins any two non-adjacent vertices of a polygon. So, we can draw the diagonals in a polygon when we directly join any two vertices which are not joined by any side. Let us learn more about the diagonal line, how to find the number of diagonals in a polygon, the diagonals of a triangle, if any, and the diagonals of a quadrilateral, along with some diagonal examples.

1.	What is a Diagonal?
2.	Diagonals of Polygons
3.	Number of Diagonals in a Polygon
4.	Length of a Diagonal
5.	FAQs on Diagonals

What is a Diagonal?

A diagonal is a straight line that connects the opposite corners of a polygon through its vertices. In other words, the diagonal of a polygon is a line segment that joins any two non-adjacent corners. Different polygons may have different number of diagonals depending on the number of sides of the polygon.

Diagonal Shape

Since a diagonal is a line segment joining non-adjacent vertices or corners, the shape of a diagonal is that of a straight line.

Diagonals of Polygons

The diagonal of a polygon is a line segment that connects any two non-adjacent vertices. Depending upon the type of polygon and the number of sides, the number of diagonals and their properties vary.

Let us now learn more about the diagonals of different polygons.

Diagonals of a Triangle

A triangle is defined as a closed shape that has 3 sides, 3 angles, and 3 vertices.It is the simplest type of polygon. No vertices in a triangle are non-adjacent. It means that there are no line segments that can form diagonals. Therefore, the number of diagonals of a triangle = 0. In other words, there are no diagonals in a triangle.

Diagonals of a Quadrilateral

We know that a quadrilateral is a four-sided polygon which means that if we join the two opposite vertices in it we get to form 2 diagonals and not more than that. In other words, there are 2 diagonals in a quadrilateral, whether it is a square, a rectangle, or a rhombus.

Diagonals of a Square

A square is defined as a closed two-dimensional figure having four sides and four corners. The opposite sides are parallel to each other and all the sides are of equal length. The diagonal of a square is a line segment that joins any two of its opposite vertices. Observe the following square and its diagonals to relate the facts given below:

• The number of diagonals of a square = 2
• By joining the opposite vertices, we get two diagonals, AC and BD.
• The length of the diagonals AC and BD in the given square is the same.
• One diagonal of a square divides it into two equal right triangles, such that the diagonal becomes the hypotenuse of the right-angled triangles so formed.

Diagonals of a Rectangle

The diagonal of a rectangle is a line segment that joins any two of its non-adjacent vertices. Observe the following rectangle, in which AC and BD are the diagonals. We can see that AC and BD are of the same length. A diagonal divides a rectangle into 2 right triangles, and the diagonals become the hypotenuse of these right-angled triangles.

Diagonals of a Rhombus

The diagonals of a rhombus are the line segments joining the opposite vertices, bisecting each other at a 90° angle, which means that the two halves of any diagonal will be of the same length. A rhombus can be defined as a diamond-shaped quadrilateral having four equal sides.

Diagonals of a Pentagon

A pentagon is a closed two-dimensional figure with five sides and five corners. The length of all five sides is equal in a regular pentagon. A pentagon has 5 diagonals as shown in the figure given below.

Diagonals of a Hexagon

A hexagon is a closed two-dimensional figure with six sides and six corners. The length of all six sides is equal in a regular hexagon. A hexagon has 9 diagonals as shown in the following figure.

Diagonals of 3D Shapes

Just like polygons, 3D shapes also have diagonals. Since they are three-dimensional figures, they have body diagonals (space diagonals) and face diagonals. The number of diagonals and their properties vary for different solids, based on the number of edges. Let us learn more about the diagonal of a cube and the diagonal of a cuboid.

Diagonals of a Cube

A cube is a three-dimensional solid figure, also known as a square solid that has edges of the same length. This means that the length, width, and height of a cube are equal, and all its faces are squares. The body diagonal of a cube is the line segment that cuts through its center, joining the opposite vertices. While the face diagonal is the one joining the opposite vertices on every face.

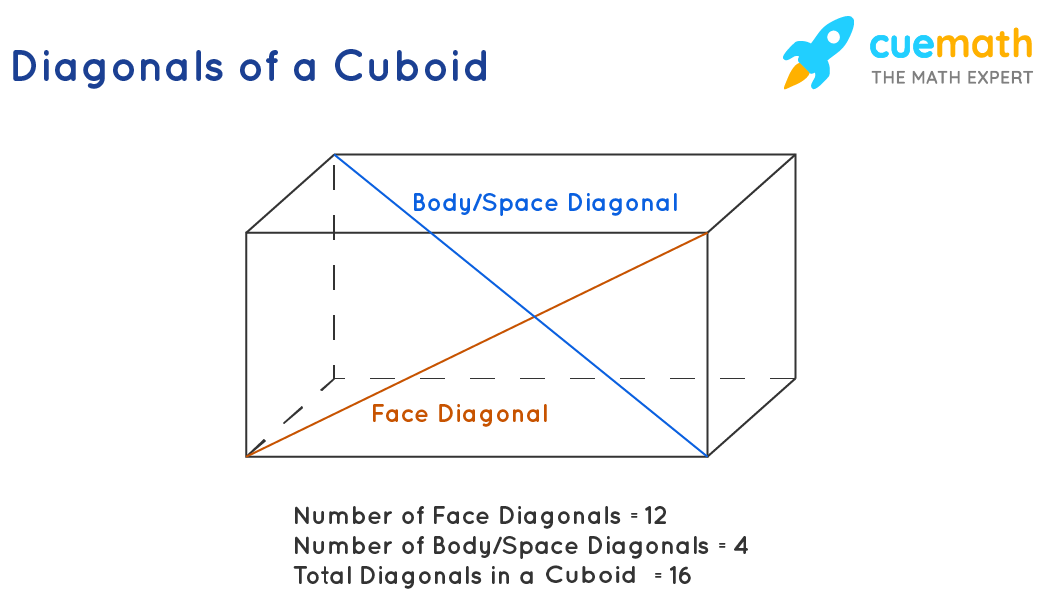
Diagonals of a Cuboid

A cuboid is a three-dimensional form of a rectangle. The body diagonal of a cuboid is the one that cuts through the center of the cuboid; while the face diagonal is the one joining the opposite vertices on every face.

Number of Diagonals in a Polygon

The number of diagonals in a polygon differs according to the type of polygon, based on the number of sides. The formula that is used to find the number of diagonals in a polygon is,

Number of diagonals = n(n - 3)/2

Here, 'n' represents the number of sides of the polygon. We can use this formula to find the number of diagonals of any polygon without actually drawing them.

The following table shows the number of diagonals of some polygons which is calculated using this formula.

Shape	Number of sides (n)	Number of Diagonals
Triangle	3	3(3 - 3)/2 = 0
Quadrilateral	4	4(4 - 3)/2 = 2
Pentagon	5	5(5 - 3)/2 = 5
Hexagon	6	6(6 - 3)/2 = 9
Heptagon	7	7(7 - 3)/2 = 14
Octagon	8	8(8 - 3)/2 = 20
Nonagon	9	9(9 - 3)/2 = 27
Decagon	10	10(10 - 3)/2 = 35
Hendecagon	11	11(11 - 3)/2 = 44
Dodecagon	12	12(12 - 3)/2 = 54

Example: Find the number of diagonals in a decagon.

Solution:

The number of sides in a decagon is n = 10. The number of diagonals of a decagon is calculated using the formula:

n(n - 3)/2 = 10(10 - 3)/2 = 10(7)/2 = 70/2 = 35

Therefore, the number of diagonals of a decagon = 35

Length of a Diagonal

The length of a diagonal for any polygon depends upon the type of polygon. There is no general formula to calculate the length of a diagonal. Rather, based on the dimensions of the particular polygon, the formula to calculate the length of the diagonal can be derived. The following section will cover the formula that is used to calculate the length of the diagonal for some polygons and solids based on their structure and dimensions.

Length of Diagonal of Square

The length of the diagonal of a square can be calculated using the Pythagoras theorem. Since the diagonal of a square divides the square into two right-angled triangles, the diagonal acts as a hypotenuse. So, applying the Pythagoras theorem, we can find the diagonal length using the formula, Diagonal (d) = √(x2 + x2); where 'd' is the diagonal, and 'x' represents the side length. This formula further reduces to, d = √(x2 + x2) = √(2x2) = √2x

Length of diagonal of a square = √2x

Length of Diagonal of a Rectangle

The length of a diagonal of a rectangle can be calculated using the Pythagoras theorem because the diagonal of a rectangle divides the rectangle into two right-angled triangles. So, the diagonal acts as the hypotenuse, and the formula that is derived is, d2 = l2 + w2. This further makes it, Length of a diagonal of a rectangle (d) = √(l2 + w2); where 'l' represents the length and 'w' represents the width (breadth) of the rectangle.

Length of a Diagonal of a Cube

A cube has 6 faces and each face of a cube is a square. Thus, each face has two diagonals. Consider a cube of length x units. So, using the Pythagoras theorem, the length of each face diagonal of cube = √2x

Apart from the diagonals on the faces, there are 4 other diagonals (body diagonals) that pass through the center of the square. The formula for the length of the diagonal of a cube is derived in the same way as we derive the length of the diagonal of a square. Length of body diagonal of a cube = √3x

Length of a Diagonal of a Cuboid (Rectangular Prism)

Consider a cuboid of length l, width w, and height h. Let us assume that its body diagonal that passes through the center of the cuboid is 'd'. Length of the body diagonal of a cuboid = √(l2 + w2 + h2).

Important Notes on Diagonals

• The number of diagonals of a polygon can be calculated with the formula, Number of diagonals = n(n - 3)/2; where 'n' represents the number of sides in the polygon.
• The length of the diagonal of a rectangle with sides 'l' and 'w' is calculated with the formula, diagonal (d) = √(l2 + w2)
• The length of the diagonal of a cube is calculated with the formula, diagonal (d) = √3x; where 'x' is the side of a cube.
• The length of the diagonal of a cuboid of sides l, w, and h, is calculated with the formula, d = √(l2 + w2 + h2)

☛ Related Topics

• Closed Shapes
• Concave Shapes
• Convex Shapes
• Diagonals Formula
• Diagonal of a Polygon Formula
• Diagonal of a Square Formula
• Diagonal of a Rectangle Calculator